 |
Параметрические преобразования сигналов
|
|
|
|
В уравнении (7.1), описывающем прохождение электрического сигнала через цепь, коэффициенты an имеют физический смысл параметров этой цепи. Если эти коэффициенты зависят от времени, цепь называется параметрической. Зависимость от времени означает возможность управления параметром цепи внешним, обычно электрическим, сигналом. В радиотехнических цепях находят применение следующие параметрические элементы: резисторы, конденсаторы, катушки индуктивности. В качестве параметрической также может быть использована нелинейная цепь, работающая в определенном режиме, усилитель с управляемым коэффициентом передачи, либо аналоговый перемножитель, выпускаемый в виде отдельной интегральной микросхемы или входящий в состав более сложных микросхем. Наиболее простой параметрической цепью является регулируемый делитель напряжения на рис.7.13.
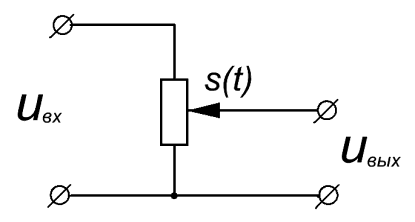
Рис.7.13. Параметрическая цепь в виде регулируемого делителя напряжения.
Выходное напряжение является функцией как входного сигнала  , так и коэффициента передачи, который регулируется (управляется) внешним электрическим сигналом
, так и коэффициента передачи, который регулируется (управляется) внешним электрическим сигналом 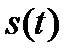 :
: 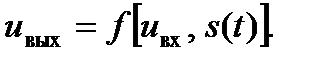 . При этом коэффициент передачи, являющийся параметром цепи, зависит от времени:
. При этом коэффициент передачи, являющийся параметром цепи, зависит от времени: 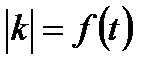 . Необходимо отметить, что частота управляющего сигнала должна быть сравнимой с частотой входного сигнала, в противном случае (например, при медленном ручном регулировании) цепь будет являться квазилинейной, т.е. спектры входного и выходного сигналов будут практически одинаковыми.
. Необходимо отметить, что частота управляющего сигнала должна быть сравнимой с частотой входного сигнала, в противном случае (например, при медленном ручном регулировании) цепь будет являться квазилинейной, т.е. спектры входного и выходного сигналов будут практически одинаковыми.
В качестве параметрической может быть использована нелинейная цепь с квадратичной вольтамперной характеристикой, показанной на рис.7.14. Если ток I пропорционален квадрату напряжения u2, то крутизна вольтамперной характеристики линейно зависит от напряжения смещения:
|
|
|
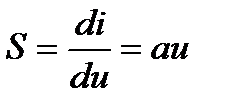 . (7.13)
. (7.13)
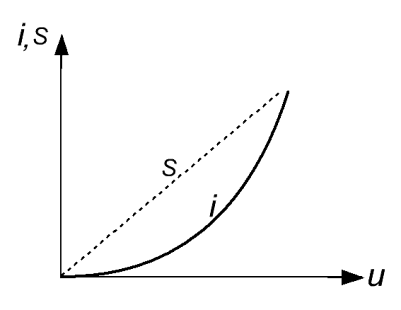
Рис.7.14. Вольтамперная характеристика нелинейной цепи.
Если на такую цепь подать постоянное напряжение смещения и входной сигнал, амплитуда которого сравнима со смещением 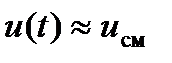 (рис.7.15а), то цепь будет нелинейной. Если же входной сигнал будет достаточно малым
(рис.7.15а), то цепь будет нелинейной. Если же входной сигнал будет достаточно малым 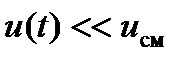 (рис.7.15б), то нелинейностью вольтамперной характеристики в пределах двойной амплитуды сигнала можно пренебречь и для такого сигнала цепь будет квазилинейной. При изменении напряжение смещения будет изменяться крутизна
(рис.7.15б), то нелинейностью вольтамперной характеристики в пределах двойной амплитуды сигнала можно пренебречь и для такого сигнала цепь будет квазилинейной. При изменении напряжение смещения будет изменяться крутизна 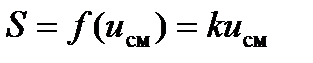 вольтамперной характеристики и, следовательно, амплитуда выходного тока
вольтамперной характеристики и, следовательно, амплитуда выходного тока 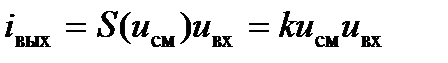 и цепь станет параметрической.
и цепь станет параметрической.

Рис7.15. Нелинейный и параметрический режим работы нелинейной цепи
Модуляция сигналов
Одним из часто применяемых параметрических преобразований является модуляция. Модуляция – процесс медленного, по сравнению с периодом сигнала, изменения во времени одного или нескольких параметров, характеризующих данный сигнал. Уравнение, описывающее гармонический сигнал,
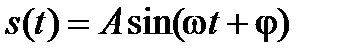 (7.14.)
(7.14.)
содержит три параметра этого сигнала: амплитуду 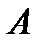 , частоту
, частоту 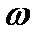 и начальную фазу
и начальную фазу  . При амплитудной модуляции происходит управление амплитудой сигнала, при частотной – его частотой, а при фазовой – начальной фазой сигнала. Графические изображения сигналов при разных видах модуляции приведены на рис.7.16, при этом для наглядности управляющий (модулирующий) сигнал выбран в виде прямоугольных импульсов.
. При амплитудной модуляции происходит управление амплитудой сигнала, при частотной – его частотой, а при фазовой – начальной фазой сигнала. Графические изображения сигналов при разных видах модуляции приведены на рис.7.16, при этом для наглядности управляющий (модулирующий) сигнал выбран в виде прямоугольных импульсов.
Так как частота и начальная фаза тесно связаны друг с другом
выражением  , то частотная и фазовая модуляции также взаимосвязаны. Иногда их объединяют под общим названием «угловой модуляции».
, то частотная и фазовая модуляции также взаимосвязаны. Иногда их объединяют под общим названием «угловой модуляции».
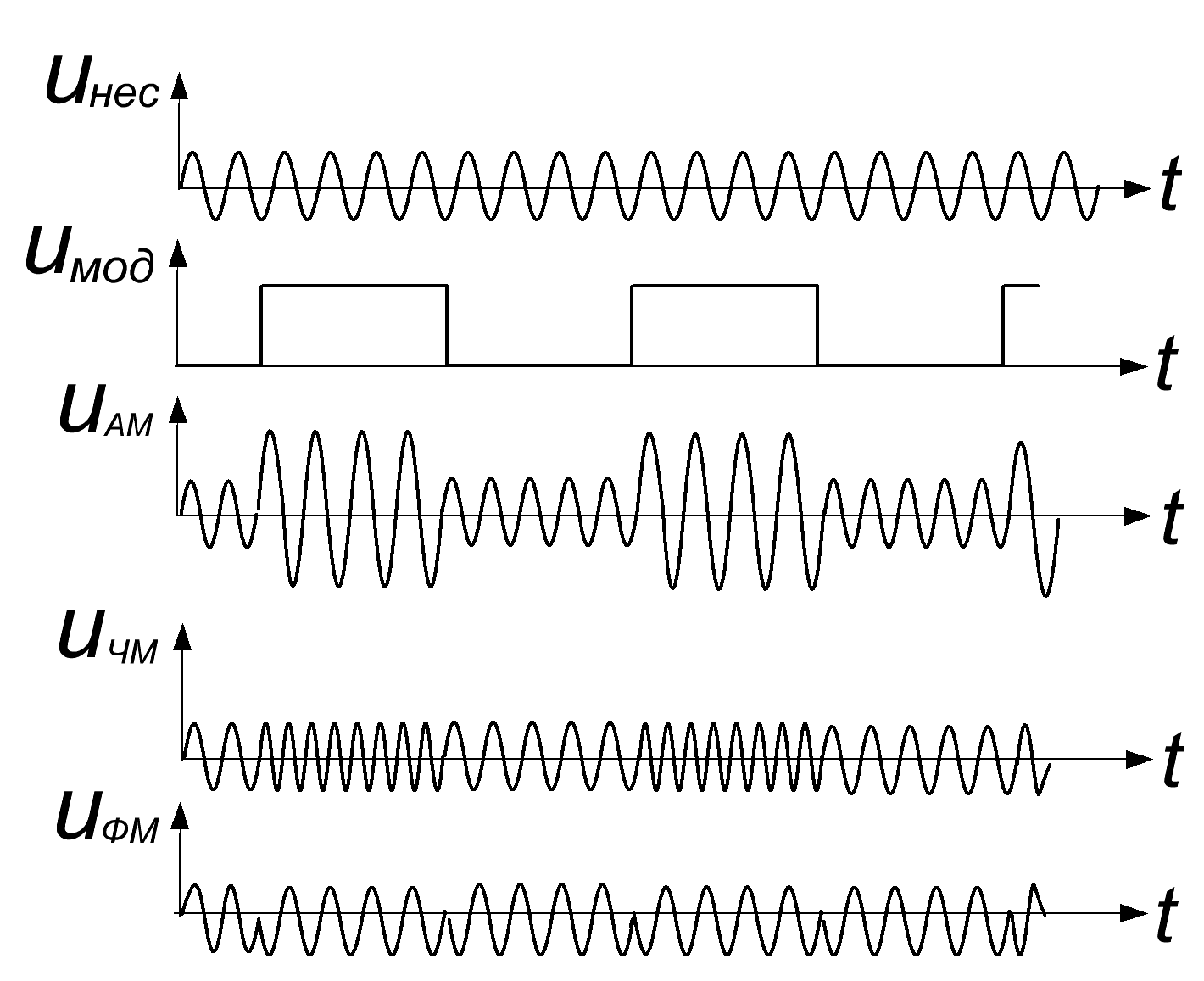
Рис.7.16. Сигналы с амплитудной, частотной и фазовой модуляцией
Амплитудная модуляция широко применяется для передачи сообщений в радиодиапазонах длинных, средних и коротких волн, а также для передачи видеосигналов в телевидении. При амплитудной модуляции передаваемый сигнал изменяет (модулирует) амплитуду несущего колебания, при этом спектр передаваемого сообщения сдвигается вверх по оси частот на величину частоты несущего колебания. Несущие колебания разных передающих устройств различаются по частоте, что позволяет осуществлять одновременную передачу множества сообщений без взаимных помех.
|
|
|
Уравнение амплитудно-модулированного сигнала имеет вид
 , (7.15)
, (7.15)
где: U 0 – амплитуда несущего колебания; ω0 – частота несущего колебания; Ω. – частота модулирующего колебания; m – коэффициент модуляции.
Коэффициент глубины модуляции равен
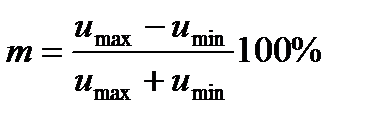 , (7.16)
, (7.16)
где  , (7.17)
, (7.17)
 (7.18)
(7.18)
Амплитудно-модулированное колебание показано на рис.7.17.

Рис.7.17. Амплитудно-модулированный сигнал
Спектр АМ сигнала показан на рис.7.18 и содержит составляющую с частотой несущего колебания и два боковых колебания с частотами  и
и 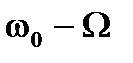 .
.

Рис.7.18. Спектр амплитудно-модулированного сигнала
При модуляции сигналом сложной формы вместо боковых частот появляются боковые полосы частот, расположенные симметрично относительно несущей частоты, как показано на рис.7.19.
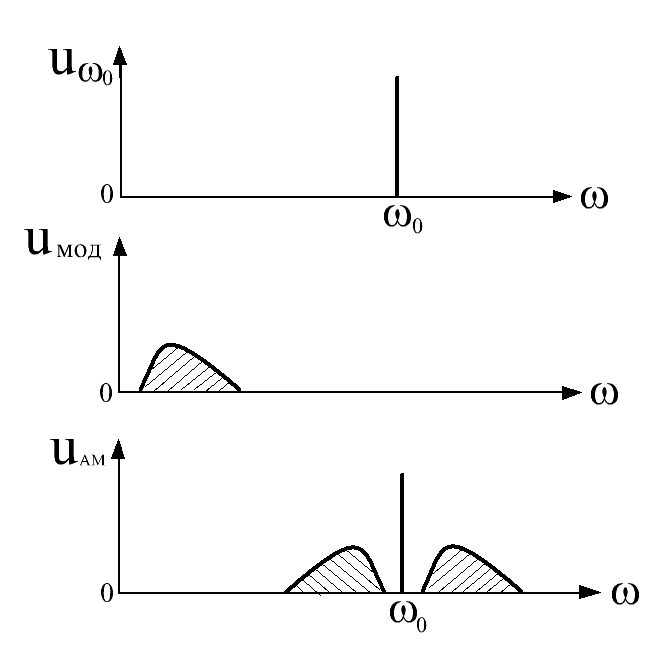
Рис.7.19. Спектр амплитудно-модулированного сигнала при модуляции сигналом сложной формы
Амплитудным модулятором называется устройство, огибающая высокочастотного сигнала на выходе которого пропорциональна низкочастотному модулирующему колебанию.
Балансная модуляция
В спектре амплитудно-модулированного сигнала передаваемая информация содержится только в боковых полосах, несущая же полезной информации не несет. Поэтому иногда выгодно не тратить энергию на передачу «бесполезной» несущей (на самом деле несущая необходима при демодуляции передаваемого сигнала).
Амплитудная модуляция с подавленной несущей называется балансной модуляцией или DoubleSideBand (DSD). Для ее осуществления на один вход аналогового перемножителя подается сигнал несущей, а на второй - сигнал огибающей без постоянной составляющей. При этом
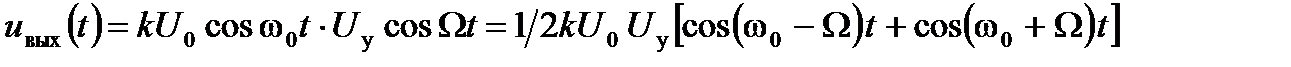 . (7.24)
. (7.24)
Спектр этого сигнала не содержит несущей, а только две боковые частоты или полосы. Вид балансно-модулированного сигнала и его спектр показаны на рис.7.23 и 7.24 соответственно.
|
|
|

Рис.7.23. Балансно-модулированный сигнал

Рис.7.24. Спектр балансно-модулированного сигнала
Видно, что балансный модулятор отличается от амплитудного отсутствием постоянной составляющей, которая суммируется с модулирующим сигналом.
26
ДЕТЕКТИРОВАНИЕ СИГНАЛОВ
На основе нелинейных цепей осуществляется детектирование (демодуляция) амплитудно-модулированных (АМ) сигналов в радиоприемниках. Схема амплитудного детектора и принцип его работы поясняются на рис.7.9.
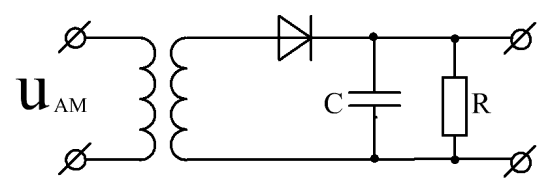
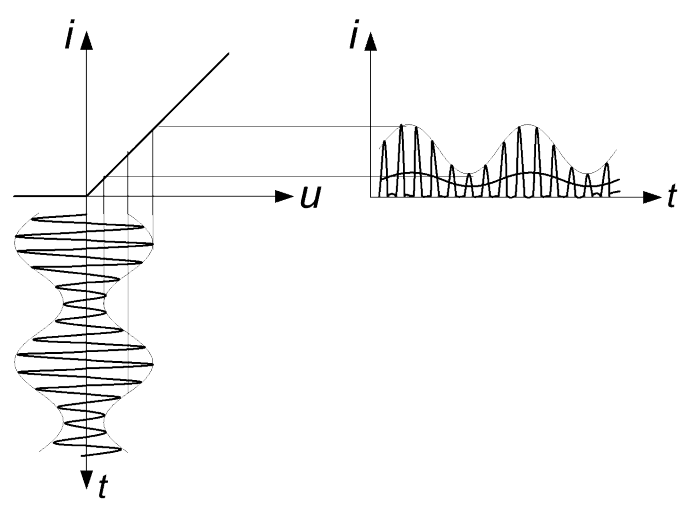
Рис.7.9. Схема амплитудного детектора и форма выходного тока
Нелинейный элемент, вольтамперная характеристика которого аппроксимирована ломаной линией, пропускает только одну (в данном случае положительную) полуволну входного тока. Эта полуволна создает на резисторе 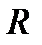 импульсы напряжения высокой (несущей) частоты с огибающей, воспроизводящей форму огибающей амплитудно-модулированного сигнала. Спектр напряжения на резисторе содержит частоту несущей
импульсы напряжения высокой (несущей) частоты с огибающей, воспроизводящей форму огибающей амплитудно-модулированного сигнала. Спектр напряжения на резисторе содержит частоту несущей 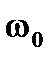 , ее гармоники и низкочастотную составляющую, которая примерно вдвое меньше амплитуды импульсов напряжения. Эта составляющая имеет частоту
, ее гармоники и низкочастотную составляющую, которая примерно вдвое меньше амплитуды импульсов напряжения. Эта составляющая имеет частоту  , равную частоте огибающей, т.е. представляет собой продетектированный сигнал. Конденсатор
, равную частоте огибающей, т.е. представляет собой продетектированный сигнал. Конденсатор 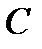 совместно с резистором
совместно с резистором 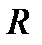 образует фильтр низких частот. При выполнении условия
образует фильтр низких частот. При выполнении условия
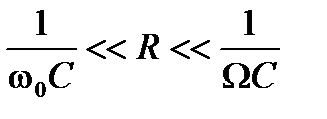 (7.12)
(7.12)
в спектре выходного напряжения остается только частота огибающей. При этом также происходит увеличение выходного напряжения за счет того, что при положительной полуволне входного напряжения конденсатор  быстро заряжается через малое сопротивление открытого нелинейного элемента почти до амплитудного значения входного напряжения, а при отрицательной полуволне – не успевает разрядиться через большое сопротивление резистора
быстро заряжается через малое сопротивление открытого нелинейного элемента почти до амплитудного значения входного напряжения, а при отрицательной полуволне – не успевает разрядиться через большое сопротивление резистора  . Приведенное описание работы амплитудного детектора соответствует режиму большого входного сигнала, при котором ВАХ полупроводникового диода аппроксимируется ломаной прямой.
. Приведенное описание работы амплитудного детектора соответствует режиму большого входного сигнала, при котором ВАХ полупроводникового диода аппроксимируется ломаной прямой.
В режиме малого входного сигнала начальный участок ВАХ диода может быть аппроксимирован квадратичной зависимостью. При подаче на такой нелинейный элемент амплитудно-модулированного сигнала, спектр которого содержит несущую и боковые частоты, возникают частоты с суммарной и разностной частотами. Разностная частота представляет собой продетектированный сигнал, а несущая и суммарная частоты не проходят через фильтр низких частот, образованный элементами  и
и  .
.
|
|
|
Обычный прием детектирования частотно-модулированных (ЧМ) колебаний состоит в том, что ЧМ колебание сначала преобразуется в АМ колебание, которое затем детектируется вышеописанным способом. В качестве простейшего преобразователя ЧМ в АМ может служить расстроенный относительно несущей частоты колебательный контур. Принцип преобразования ЧМ сигналов в АМ поясняется на рис.7.10.
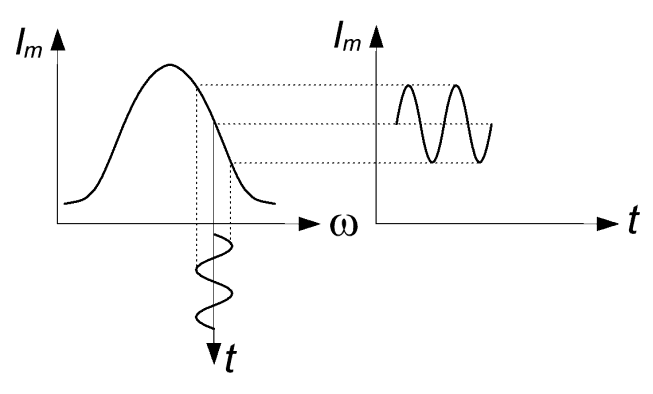
Рис.7.10. Преобразование ЧМ в АМ
При отсутствии модуляции рабочая точка находится на скате резонансной кривой контура. При изменении частоты изменяется амплитуда тока в контуре, т.е. происходит преобразование ЧМ в АМ.
Схема преобразователя ЧМ в АМ показана на рис.7.11.

Рис.7.11. Преобразователь ЧМ в АМ
Недостатком такого детектора являются искажения продетектированного сигнала, возникающие из-за нелинейности резонансной кривой колебательного контура. Поэтому на практике применяются симметричные схемы, обладающие лучшими характеристиками. Пример такой схемы приведен на рис.7.12.

Рис.7.12. Детектор ЧМ сигналов
Два контура настраиваются на крайние значения частоты, т.е. на частоты 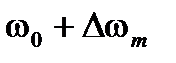 и
и 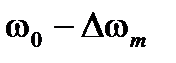 . Каждый из контуров преобразует ЧМ в АМ, как описано выше. АМ колебания детектируются соответствующими амплитудными детекторами. Низкочастотные напряжения
. Каждый из контуров преобразует ЧМ в АМ, как описано выше. АМ колебания детектируются соответствующими амплитудными детекторами. Низкочастотные напряжения  и
и 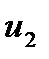 противоположны по знаку, и с выхода схемы снимается их разность. Характеристика детектора, т.е. зависимость выходного напряжения от частоты, получается путем вычитания двух резонансных кривых и более линейна. Такие детекторы называются дискриминаторами (различителями).
противоположны по знаку, и с выхода схемы снимается их разность. Характеристика детектора, т.е. зависимость выходного напряжения от частоты, получается путем вычитания двух резонансных кривых и более линейна. Такие детекторы называются дискриминаторами (различителями).
Линейный детектор
Амплитудный детектор, выполненный на нелинейной цепи с полупроводниковым диодом, имеет нелинейную зависимость выходного (продетектированного) напряжения от амплитуды входного напряжения. Это связано с нелинейностью вольтамперной характеристики диода. При использовании диодного детектора в радиоприемнике этот недостаток малозаметен. Однако, при детектировании, например, телевизионного сигнала нелинейность детектора проявляется в виде нарушения соотношений яркости разных частей изображения, что недопустимо. В таких случаях необходим линейный амплитудный детектор, который может быть выполнен на аналоговом перемножителе. Принцип его работы показан на рис.7.31.
|
|
|
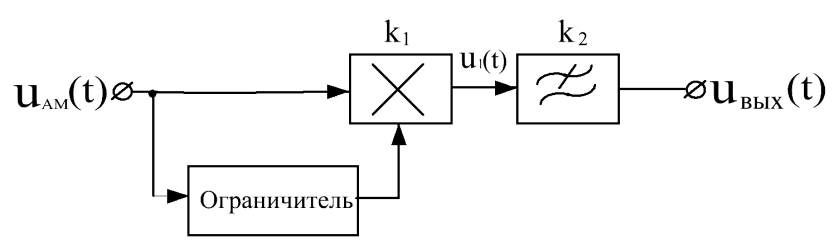
Рис.7.31. Линейный детектор
Амплитудно-модулированный сигнал 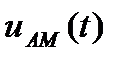 подается на один из входов перемножителя. На второй вход подается этот же сигнал, но прошедший через двухсторонний ограничитель и поэтому имеющий постоянную амплитуду
подается на один из входов перемножителя. На второй вход подается этот же сигнал, но прошедший через двухсторонний ограничитель и поэтому имеющий постоянную амплитуду  . После перемножения и фильтрации удвоенной частоты несущей получается напряжение, прямо пропорциональное амплитуде входного сигнала
. После перемножения и фильтрации удвоенной частоты несущей получается напряжение, прямо пропорциональное амплитуде входного сигнала
 (7.31)
(7.31)
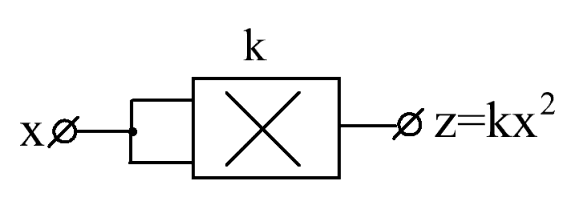
Рис.7.33. Схема возведения в квадрат(квадратичный детектор)
27
ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ
Преобразованием частоты является любое ее изменение. Например, при выпрямлении переменный ток с частотой превращается в постоянный ток, у которого частота равна нулю. В генераторах энергия постоянного тока, имеющего частоту, равную нулю, преобразуется в энергию переменного тока нужной частоты.
Вспомогательное напряжение получают от маломощного генератора, называемого гетеродином. На выходе преобразователя получается колебание с новой преобразованной частотой, которую называют промежуточной частотой.
В качестве преобразователя частоты должен применяться нелинейный или параметрический прибор.
Если бы преобразователь частоты был линейным прибором, то в нем бы произошло бы просто сложение двух колебаний. Например, при сложении двух колебаний с близкими, но не кратными частотами получились бы биения, т. е. сложное колебание, у которого частота менялась бы в некоторых пределах около среднего значения, а амплитуда изменялась бы с частотой, равной разности частот. Такие биения не содержат составляющего колебания с новой частотой. Но если биения детектировать (выпрямить), то вследствие нелинейности этого процесса возникает составляющая с промежуточной частотой.
На выходе преобразователя частоты получается сложное колебание, имеющее составляющие многих частот.
Все новые частоты, представляющие собой комбинации частот и их гармоник, называются комбинационными частотами. Выбирая подходящую вспомогательную частоту, можно получить новую частоту.!
Среди новых частот содержатся и гармоники первоначальных колебаний с частотами в несколько раз больше исходных. Но их можно получить проще при нелинейном искажении одного из подводимых напряжений. Наличие двух напряжений для возникновения гармоник необязательно.
Как правило, амплитуды комбинационных колебаний (и гармоник) тем меньше, чем выше значения частот. Поэтому в большинстве случаев в качестве колебания новой промежуточной частоты используют колебание разностной частоты, а иногда суммарной. Комбинационные частоты более высокого порядка применяются редко.
Преобразование частоты в радиоприемниках в большинстве случаев осуществляется так, что при приеме сигналов различных радиостанций, работающих на разных частотах, создаются колебания одной и той же промежуточной частоты. Это позволяет получить большое усиление и высокую избирательность, причем они остаются почти постоянными во всем диапазоне частот принимаемых сигналов. Кроме того, при постоянной промежуточной частоте получается более устойчивая работа усилительных каскадов и они значительно проще по устройству, нежели каскады, рассчитанные на диапазон частот.
В радиоприемных и радиоизмерительных устройствах в качестве промежуточной чаще всего используется разностная частота, причем вспомогательная частота обычно выше преобразуемой частоты сигнала. Такое соотношение между частотами обязательно, если промежуточная частота должна быть выше частоты сигнала.
|
|
|


