 |
Длинная линия без потерь. Волновые уравнения.
|
|
|
|
Рассмотрим бесконечно малый отрезок  длинной линии без потерь.
длинной линии без потерь.


Рис.3.23. Эквивалентная схема отрезка лини без потерь
Приращение напряжения и тока на отрезке  можно представить в виде дифференциалов:
можно представить в виде дифференциалов:
 , (3.116)
, (3.116)
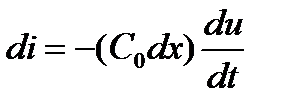 . (3.117)
. (3.117)
Разделим эти приращения на  :
:
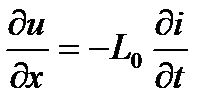 , (3.118)
, (3.118)
 . (3.119)
. (3.119)
Два последних выражения являются основными дифференциальными уравнениями линии без потерь. Частные производные обусловлены тем, что ток и напряжение зависят не только от времени, но меняются и по длине линии, т.е. зависят от координаты x.
Продифференцировав обе части первого уравнения по x и обе части второго уравнения по t, получим:
 , (3.120)
, (3.120)
 . (3.121)
. (3.121)
Подставляя (3.121) в (3.120), приходим к волновому уравнению для напряжения в линии:
 . (3.122)
. (3.122)
Дифференцируя уравнение (3.118) по  , а уравнение (3.119) по
, а уравнение (3.119) по  , получим волновое уравнение для тока в линии:
, получим волновое уравнение для тока в линии:
 , (3.123)
, (3.123)
 , (3.124)
, (3.124)
 . (3.125)
. (3.125)
Волновые уравнения для напряжения и тока можно переписать в следующем виде:
 , (3.126)
, (3.126)
 , (3.127)
, (3.127)
где  - скорость распространения электромагнитной волны в линии.
- скорость распространения электромагнитной волны в линии.
Из волновых уравнений видно, что изменения напряжения и тока управляются совершенно одинаковыми закономерностями.
Решения волновых уравнений зависят от начальных и граничных условий. Решением волнового уравнения для напряжения является любая функция вида:
 , (3.128)
, (3.128)
где  -дважды дифференцируемая функция.
-дважды дифференцируемая функция.
Решением волнового уравнения для тока будет функция  .
.
Полные решения волновых уравнений имеют вид:
 , (3.134)
, (3.134)
 . (3.135)
. (3.135)
Функции  связана с функцией
связана с функцией  следующим соотношением:
следующим соотношением:
 , (3.136)
, (3.136)
где
 (3.137)
(3.137)
- волновое сопротивление линии.
Для линии без потерь волновое сопротивление равно отношению  и является чисто активным сопротивлением.
и является чисто активным сопротивлением.
Аналогично
 (3.138)
(3.138)
|
|
|
следовательно,
 . (3.139)
. (3.139)
Таким образом, ток и напряжение в линии представлены в виде суммы прямой и обратной волн, распространяющихся по линии в противоположных направлениях со скоростью  . Для воздушной линии эта скорость равна скорости света. В кабельных линиях скорость распространения значительно ниже скорости света. Линия без потерь передаёт волны без затухания и искажений. Эти волны называются бегущими. Итак, отличительное свойство систем с распределенными параметрами состоит в том, что ток и напряжение являются функциями двух переменных
. Для воздушной линии эта скорость равна скорости света. В кабельных линиях скорость распространения значительно ниже скорости света. Линия без потерь передаёт волны без затухания и искажений. Эти волны называются бегущими. Итак, отличительное свойство систем с распределенными параметрами состоит в том, что ток и напряжение являются функциями двух переменных  и
и  , и описываются уравнениями в частных производных.
, и описываются уравнениями в частных производных.

Рис.3.24. Прямая и обратная волна в длинной линии.
Если в каком-то сечении бесконечно длинной линии без потерь включить генератор напряжения, создающий импульс, то в линии будут распространяться две волны в противоположных направлениях, как показано на рис.3.24.
Если в начале линии включить генератор гармонической э.д.с.  , то напряжение в любом сечении линии также будет гармоническим, поэтому можно записать:
, то напряжение в любом сечении линии также будет гармоническим, поэтому можно записать:  и
и  . С учетом этого волновое уравнение для напряжения можно записать в следующем виде:
. С учетом этого волновое уравнение для напряжения можно записать в следующем виде:
 , (3.140)
, (3.140)
где  - волновое число.
- волновое число.
Решение дифференциального уравнения (3.140) имеет вид:
 (3.141)
(3.141)
Второе слагаемое уравнения представляет собой прямую волну напряжения, распространяющуюся вдоль оси  вправо от начала линии, а первое слагаемое – обратную волну напряжения, распространяющуюся в противоположном направлении. Постоянные A и B можно определить из граничных условий. При некоторых условиях обратная волна в линии будет отсутствовать. При этом решение уравнения будет представлено только одним слагаемым:
вправо от начала линии, а первое слагаемое – обратную волну напряжения, распространяющуюся в противоположном направлении. Постоянные A и B можно определить из граничных условий. При некоторых условиях обратная волна в линии будет отсутствовать. При этом решение уравнения будет представлено только одним слагаемым:
 . (3.142)
. (3.142)
Постоянную  определим из граничного условия в начале линии
определим из граничного условия в начале линии
 . (3.143)
. (3.143)
Положив в (3.142)  =0, получим
=0, получим  и выражение для синусоидальной волны напряжения, распространяющейся от начала линии,
и выражение для синусоидальной волны напряжения, распространяющейся от начала линии,
 . (3.144)
. (3.144)
На рис.3.25 изображены распределения напряжения в линии для двух моментов времени  и
и  .
.
|
|
|
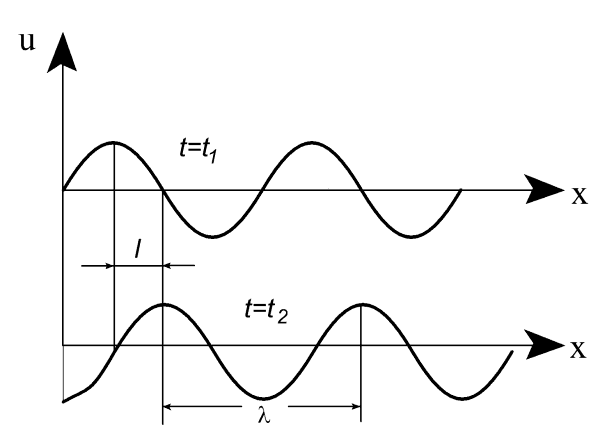
Рис.3.25. Напряжение в линии в два последовательных момента
За время 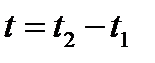 волна пробегает путь
волна пробегает путь  . Длина волны
. Длина волны  . (3.145)
. (3.145)
Фаза напряжения на расстоянии x от генератора определяется выражением
 . (3.146)
. (3.146)
29
|
|
|


