 |
Движению жидкости в трубах при турбулентном режиме. Местные гидравлические сопротивления
|
|
|
|
Задача 9
Из закрытого бака A под постоянным манометрическим давлением рати вода подается через стальную трубу, коэффициент абсолютной шероховатости которой k = 2 мм, в открытый резервуар Б, из которого она вытекает через цилиндрический насадок в атмосферу (рис. 9). Определить расход воды Q и высоту уровней h1 и h2 двумя способами, пользуясь уравнением Д. Бернулли (первый способ) и формулами расхода для истечения жидкости из отверстий и через насадки (второй способ).
Рис. 9
Дано: р = 2,4 кГ/см2,L = 100 м, dT = 200 мм, dн = 200 мм, H = 8 м.
Определить: Q, h1 и h2 двумя способами.
Решение
1. Уравнение Д. Бернулли составим для сечений 1-1 и 2-2, приняв за плоскость сравнения уровень воды O1-O1 (жидкости) в баке Б:
Так как за плоскость сравнения нами принят уровень воды в баке Б, то соответственно для сечения 1-1: z1 = h1, p1 = p, V1 = VA» 0; для сечения 2-2: z2 = 0, p2 = pа, V2 = VБ» 0;
потеря напора 
где VT – скорость в трубе;
тогда уравнение Д. Бернулли перепишется так:
откуда
где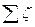 
– сумма коэффициентов местных сопротивлений, которая слагается из коэффициентов сопротивления входа, колена и выхода, то есть: 
.
Из справочника или курса гидравлики имеем:
тогда получим:
Задаемся величиной коэффициента гидравлического трения, принимая, что
Тогда
и уравнение Д. Бернулли для сечений 1-1 и 2-2 окончательно будет иметь следующий вид:
Далее составляем уравнение Д. Бернулли для сечений 2-2 и 3-3, приняв за плоскость сравнения плоскость, проходящую через ось цилиндрического насадка:
где h r – местные потери напора для цилиндрического насадка.
Так как за плоскость сравнения принята плоскость, проходящая через ось насадка, то соответственно:
|
|
|
для сечения 2-2: z1 = h2, p1 = pa,V1 = V
для сечения 3-3: z2 = 0, p2 = pa, V2 = Vцн, hr = zцн * Vцн2 / 2g.
Исходя из этого, уравнение Д. Бернулли для сечений 2-2 и 3-3 перепишется в следующем виде:
откуда
следовательно,
Итак, получили систему следующих 2-х уравнений:
.
Зная, что
ра = 1,033 кГ/см2,
получим: 
но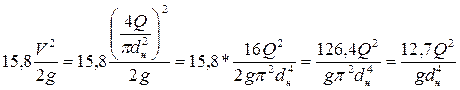 
,
поэтому:
Откуда
Получив величину расхода Q = 163,7 л/сек, вычислим скорость движения жидкости в трубе и цилиндрическом насадке по следующей формуле:
Зная скорость движения жидкости в трубе и цилиндрическом насадке, определим высоты расположения уровней воды:
2. Пользуясь формулами расхода для истечения жидкости из отверстий и через насадки, можем сказать, что по условию неразрывности движения, расходы жидкости через трубу и насадок будут одинаковыми, то есть
QT = QH;
но, зная, что
где
то
и после сокращения получим:
Зная, что 
, вычислим h1:
откуда
и 
Вычислив высоты расположения уровней жидкости, мы можем определить скорости движения жидкости в трубе и насадке по формуле:
а расход
тогда:
Разница величин h1 и h2, полученных по первому и второму способу, объясняется неточностью подсчета и лежит в пределах допустимой погрешности.
Произведем проверку правильности взятой нами величины коэффициента l = 0,025 – коэффициента гидравлического трения.
Определяем число Рейнольдса по формуле:
где для холодной воды (t = 20°C) v = 0,01 см2/сек;
Так как 1 040 000 > 2320, то режим в трубе турбулентный, и поэтому надо определить толщину ламинарного слоя «d» и в зависимости от его толщины и соотношения между k и «d» выбрать расчетную формулу для коэффициента l.
Толщину ламинарного слоя определим по следующей приближенной формуле:
где dT – диаметр трубы в мм.
Это значит, что ламинарный слой не покрывает шероховатостей стенки и ее следует считать шероховатой.
|
|
|
Так как труба металлическая и шероховатая, то коэффициент l можем определить по следующей формуле Мурина:
,
что почти совпадает с принятой выше величиной l = 0,025, ввиду чего пересчет делать не требуется. В последней формуле r – радиус трубы, k – коэффициент абсолютной шероховатости стенок трубы.
|
|
|
