 |
Волны рассеивания при падении SH-волны на кровлю высокоскоростной среды
|
|
|
|
Нижняя среда - более плотная и имеет большую скорость распространения волны, чем верхняя:.
 и
и  .
.
В соответствии с законом Снеллиуса, угол прохождения всегда больше угла падения и равному ему угла отражения:  . При изменении угле падения
. При изменении угле падения  от нуля до теоретически возможного предела 90° угол прохождения растет быстрее и становится равным 90° при
от нуля до теоретически возможного предела 90° угол прохождения растет быстрее и становится равным 90° при  . В этом случае
. В этом случае
 и
и 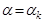 ,
,
где  - критический угол падения. При таком падении проходящая волна не уходит в глубь нижней среды, а скользит вдоль границы со скоростью
- критический угол падения. При таком падении проходящая волна не уходит в глубь нижней среды, а скользит вдоль границы со скоростью  .Эта скользящая волна порождает в верхней низкоскоростной среде вторичную волну, называемую в сейсморазведке головной или преломленной. На регистрации таких волн основан второй метод сейсморазведки - метод преломленных волн (МПВ), - первым и основным, но вторым по времени возникновения, является метод отраженных волн (МОВ).
.Эта скользящая волна порождает в верхней низкоскоростной среде вторичную волну, называемую в сейсморазведке головной или преломленной. На регистрации таких волн основан второй метод сейсморазведки - метод преломленных волн (МПВ), - первым и основным, но вторым по времени возникновения, является метод отраженных волн (МОВ).
При нормальном падении все косинусы равны единице, коэффициент отражения отрицателен, а коэффициент прохождения меньше единицы. Следовательно, в этом случае отраженная волна противоположна падающей по знаку смещений (отражение с потерей полуволны), а проходящая волна имеет меньшую амплитуду, чем волна падающая:
при α = 0 и A < 0 и  B < 1 и
B < 1 и  = B · u (τ) < u (τ).
= B · u (τ) < u (τ).
При критическом угле падения  угол прохождения
угол прохождения 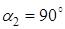 и А = 1, В = 1 + А = 2. Отраженная волна имеет ту же амплитуду, что и волна падающая, а проходящая волна по амплитуде вдвое превосходит ее:
и А = 1, В = 1 + А = 2. Отраженная волна имеет ту же амплитуду, что и волна падающая, а проходящая волна по амплитуде вдвое превосходит ее:
при  А = 1 и
А = 1 и  В = 2 и
В = 2 и  .
.
Видно, что и при  коэффициент отражения меняет свой знак: при нормальном падении А < 0, а при
коэффициент отражения меняет свой знак: при нормальном падении А < 0, а при  А = 1 > 0, и существует угол
А = 1 > 0, и существует угол  , при котором А = 0 и
, при котором А = 0 и  , В = 1 и
, В = 1 и  , - отраженной волны нет, есть только проходящая вторичная волна с амплитудой, равной амплитуде падающей волны. Синус этого угла определен ранее, но, так как
, - отраженной волны нет, есть только проходящая вторичная волна с амплитудой, равной амплитуде падающей волны. Синус этого угла определен ранее, но, так как  , формулу для
, формулу для  удобнее записать, умножив числитель и знаменатель подкоренного выражения на - 1:
удобнее записать, умножив числитель и знаменатель подкоренного выражения на - 1:
|
|
|
 .
.
При дальнейшем увеличении угла падения, когда  , коэффициент отражения А стремительно возрастает от 0 при
, коэффициент отражения А стремительно возрастает от 0 при  до 1, при
до 1, при  одновременно и также быстро В растет от 1 до 2. Однако, более существенные изменения коэффициентов А и В и вторичных волн - отраженной и проходящей - происходят, когда угол падения становится больше критического. Если
одновременно и также быстро В растет от 1 до 2. Однако, более существенные изменения коэффициентов А и В и вторичных волн - отраженной и проходящей - происходят, когда угол падения становится больше критического. Если  (напомним,
(напомним,  ), в соответствии с законом Снеллиуса:
), в соответствии с законом Снеллиуса:
 и
и 
синус угле прохождения при закритическом падении становится больше единицы (?!). Это не может быть в области действительных тригонометрических функций. Определим косинус угле прохождения по обычной формуле:
 , так как
, так как  .
.
Синусу, большему 1, соответствует чисто мнимый косинус.
Встретившись с этой неожиданной трансформацией косинуса, мы, из осторожности, записали оба возможных знака (±) корня. Установим, какой из них имеет физический смысл. Для этого вспомним описание проходящей волны (в волновой аргумент которой и входит  ) и ее спектра:
) и ее спектра:

Подставим в последнее определение
 :
:

Наличие мнимой единицы в определении косинуса выводит зависимость от z из функции запаздывания и превращает ее в амплитудный множитель  . Если определить
. Если определить  , то с ростом z (то есть, при удалении от границы и от предполагаемого источника колебаний) амплитуда гармоники частоты ω неограниченно возрастает:
, то с ростом z (то есть, при удалении от границы и от предполагаемого источника колебаний) амплитуда гармоники частоты ω неограниченно возрастает:
при z → ∞  .
.
Физически это абсолютно невозможно, поэтому из двух знаков мнимого косинуса следует выбрать минус:  . Тогда амплитуда вторичной волны, определяемая множителем
. Тогда амплитуда вторичной волны, определяемая множителем  , стремится к нулю при удалении от границы (z → ∞).
, стремится к нулю при удалении от границы (z → ∞).
Однако, спектр импульсного сигнала определен на всем бесконечном интервале частот: - ∞ ≤ ω ≤ ∞ и в волновом импульсе присутствуют как гармоники с положительными частотами, так и гармоники с ω < 0. Знак минус в определении  “правильно действует" только для положительных частот. Для отрицательных частот знак минус гаснет и амплитуда гармоники частоты ω < 0 неограниченно возрастает по мере удаления от границы z → ∞. Это - снова нереально.
“правильно действует" только для положительных частот. Для отрицательных частот знак минус гаснет и амплитуда гармоники частоты ω < 0 неограниченно возрастает по мере удаления от границы z → ∞. Это - снова нереально.
|
|
|
Чтобы обеспечить затухание всего спектра волны  как для положительных, так и для отрицательных частот, определим:
как для положительных, так и для отрицательных частот, определим:
 ,
,
где sgn (ω) - знаковая функция частоты:
 .
.
В таком определении амплитудный множитель  обеспечивает затухание гармонических составляющих со всеми частотами: если ω > 0, sgn (ω) = + 1 и
обеспечивает затухание гармонических составляющих со всеми частотами: если ω > 0, sgn (ω) = + 1 и  - функция, убывающая с ростом z, если же ω < 0, sgn (ω) = - 1 и
- функция, убывающая с ростом z, если же ω < 0, sgn (ω) = - 1 и  - так же убывающая по мере удаления от границы функция.
- так же убывающая по мере удаления от границы функция.
Обратим внимание на то, что с ростом абсолютного значения частоты ω затухание ускоряется - чем выше частота гармоники, тем быстрее она затухает с ростом z.
В функции запаздывания спектра проходящей волны  осталась лишь пространственная переменная x:
осталась лишь пространственная переменная x:  . Эта функция соответствует скольжению плоской волны
. Эта функция соответствует скольжению плоской волны  вдоль границы со скоростью
вдоль границы со скоростью  , меньшей истинной скорости
, меньшей истинной скорости  волны в нижней среде, так как
волны в нижней среде, так как  . Эта скользящая с “неправильной" скоростью волна имеет амплитуду, экспоненциально уменьшающуюся с глубиной, вдоль фронта волны. Эти две особенности закритической проходящей волны дают основание для ее специального наименования - она называется неоднородной плоской волной, в соответствии с характером распределения ее амплитуды по фронту.
. Эта скользящая с “неправильной" скоростью волна имеет амплитуду, экспоненциально уменьшающуюся с глубиной, вдоль фронта волны. Эти две особенности закритической проходящей волны дают основание для ее специального наименования - она называется неоднородной плоской волной, в соответствии с характером распределения ее амплитуды по фронту.
Неоднородные плоские волны играют главенствующую роль в образовании преломленной (головной) волны, которую рассмотрим несколько позже в отдельном разделе. Здесь подчеркнем одно - все особенности неоднородной волны выявлены в результате анализа лишь волнового аргумента проходящей волны при закритическом падении плоской волны на границу раздела. Вид самой волновой функции  этим анализом не затронут. Поэтому вернемся к исследованию поведения спектральных коэффициентов рассеивания и вторичных волн при закритическом падении первичной волны.
этим анализом не затронут. Поэтому вернемся к исследованию поведения спектральных коэффициентов рассеивания и вторичных волн при закритическом падении первичной волны.
Итак, установлено, что при

 где
где
 .
.
Коэффициенты рассеивания А и В в этом случае описываются выражениями:
|
|
|

Знаком тождества подчеркнута комплексная зависимость коэффициентов рассеивания от частоты, оправдывающая введенное ранее определение А и В как спектральных коэффициентов рассеивания.
В числителе и знаменателе дроби, определяющей А - комплексно-сопряженные выражения:  , имеющие одинаковый модуль (так как
, имеющие одинаковый модуль (так как  ) и противоположные по знаку аргументы. Поэтому модуль спектрального коэффициента выражения равен 1:
) и противоположные по знаку аргументы. Поэтому модуль спектрального коэффициента выражения равен 1:

и не зависит ни от частоты, ни от угла падения. Фазово-частотный коэффициент отражения как аргумент дроби с комплексно-сопряженными числителем и знаменателем, равен:
 .
.
Действительная realA и мнимая imageA части спектрального коэффициента отражения (СКО) равны:
 ,
,
где
 .
.
Используя формулы косинуса и синуса двойного угла ( ), получим выражения для действительной и мнимой частей СКО в виде:
), получим выражения для действительной и мнимой частей СКО в виде:
 ;
;
 .
.
Действительная часть СКО не зависит от частоты, а зависимость мнимой части от нее задается множителем в виде знаковой функции частоты. Обе части СКО являются функциями угла падения. Спектральная характеристика отражения обладает всеми свойствами устойчивой линейной системы - четными амплитудно-частотной характеристикой (модулем СКО) и действительной части СКО, и нечетными фазово-частотной характеристикой (аргументом СКО) и мнимой частью СКО. При этом, четность обеспечивается отсутствием зависимости 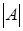 и realA от частоты, а нечетность
и realA от частоты, а нечетность  и imageA - множителем в виде знаковой функции sgn (ω). Таким образом, комплексный спектральный коэффициент отражения может быть записан в виде:
и imageA - множителем в виде знаковой функции sgn (ω). Таким образом, комплексный спектральный коэффициент отражения может быть записан в виде:
 .
.
Спектр отраженной волны разделяется на два слагаемых:
 .
.
В первом слагаемом присутствует спектр первичной волны с амплитудным множителем (весом) ReA (α), независимым от частоты и меняющимся с увеличением угла падения.
Во втором слагаемом - произведение двух частотно-зависимых функций - знаковой  и комплексного спектра первичной волны u (jf) - с амплитудным множителем ImA (α), также изменяющимся с увеличением угла падения.
и комплексного спектра первичной волны u (jf) - с амплитудным множителем ImA (α), также изменяющимся с увеличением угла падения.
|
|
|
Так как преобразование Фурье - линейная операция, сам отраженный сигнал также является взвешенной суммой Фурье-трансформант слагаемых своего спектра:
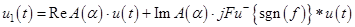 .
.
Здесь  - результат обратного Фурье-преобразования знаковой функции частоты sgn (f), u (t)
- результат обратного Фурье-преобразования знаковой функции частоты sgn (f), u (t)  u (jf), а произведение спектров заменено сверткой Фурье-трансформант сомножителей в соответствии со спектральной теоремой свертывания функций.
u (jf), а произведение спектров заменено сверткой Фурье-трансформант сомножителей в соответствии со спектральной теоремой свертывания функций.
В теории спектров рассматривалась знаковая функция времени sgn (t) и ее спектр:
 .
.
Аналогично определяется обратное Фурье-преобразование знаковой функции частоты:
 .
.
Здесь появился знак минус как следствие противоположных знаков ядер прямого ( ) и обратного (
) и обратного (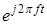 ) преобразований Фурье.
) преобразований Фурье.
Тогда отраженный сигнал может быть описан выражением:
 .
.
Сокращая мнимую единицу и раскрывая символьную запись свертки, получим описание отраженного сигнала при углах падения, превышающих критический угол:
 .
.
В скобках записано обратное Гильберт-преобразование функции u (t), описывающей первичную волну:
 .
.
Таким образом, отраженный сигнал за критическим углом падения представляется взвешенной суммой падающего сигнала u (t) и его Гильберт-трансформанты  :
:
 .
.
Веса слагаемых - ReA (α) и ImA (α) - изменяются при увеличении угла падения. Соответственно, изменяется по форме и суммарный отраженный сигнал  .
.
Проведем анализ зависимости от угла падения α весовых множителей ReA (α) и ImA (α) и структуры суммарной отраженной волны при изменении α от критического угла  до теоретически возможного предела 90°. Как отмечалось, при α =
до теоретически возможного предела 90°. Как отмечалось, при α =  А (
А ( ) = 1 = ReA (
) = 1 = ReA ( ), ImA (
), ImA ( ) = 0. Отраженная волна имеет те ж форму и амплитуду, что и падающая волна:
) = 0. Отраженная волна имеет те ж форму и амплитуду, что и падающая волна:  =
=  .
.
Как только угол падения превысит критический угол, ReA (α) стремительно уменьшается, а мнимая часть ImA (α) столь же быстро возрастает. Доля первичного сигнала в суммарной отраженной волне быстро уменьшается, и так же быстро растет доля Гильберт-трансформанты падающей волны. При некотором угле падения  действительная часть спадает до 0, а мнимая - возрастает до 1:
действительная часть спадает до 0, а мнимая - возрастает до 1:
при α =  ReA (
ReA ( ) = 0; ImA (
) = 0; ImA ( ) = 1.
) = 1.
Отраженный сигнал представлен только Гильберт-трансформантой первичной волны:  . Угол
. Угол  находится из условия ReA (
находится из условия ReA ( ) = 0:
) = 0:
 .
.
Синус его равен:

и не намного превышает  , то есть
, то есть  не намного больше
не намного больше  .
.
Дальнейшее увеличение угла падения (α >  ) приводит к перемене знака действительной части и к соответствующему инвертированию знака смещения первичной волны в суммарном отраженном сигнале.
) приводит к перемене знака действительной части и к соответствующему инвертированию знака смещения первичной волны в суммарном отраженном сигнале.
В пределе, при 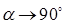 : ReA
: ReA 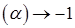 ; ImA
; ImA  и
и  .
.
С увеличением угла падения при  доля падающей волны с инвертированным знаком смещения в суммарной волне растет, а доля Гильберт-трансформанты уменьшается в пределе, при α = 90°, до 0.
доля падающей волны с инвертированным знаком смещения в суммарной волне растет, а доля Гильберт-трансформанты уменьшается в пределе, при α = 90°, до 0.
|
|
|
При этом отраженный сигнал повторяет по форме и амплитуде колебаний падающую волну с инвертированным знаком смещений. Напомним, что такой же предел был выявлен и в случае  (см. раздел 8.3), что вполне естественно.
(см. раздел 8.3), что вполне естественно.
Анализ закритических изменений спектрального коэффициента прохождения В и вызванных ими трансформаций неоднородных плоских волн  фактически не нужен, так как имеется связь между коэффициентами рассеивания SH-волны: В = 1 + А, справедливая при любых углах падения.
фактически не нужен, так как имеется связь между коэффициентами рассеивания SH-волны: В = 1 + А, справедливая при любых углах падения.
Для комплексных коэффициентов рассеивания А = ReA + jImA; B = ReB + jImB имеем:
ReB + jImB = 1 + ReA + jImA.
Видно, что А и В имеют действительные части, различающиеся на единицу, и равные мнимые части:
ReB = 1 + ReA; ImB = ImA.
Напомним, что связь между А и В получена из первого граничного условия (для упругих смещений):
 .
.
В соответствии с ним, при любых соотношениях физических свойств контактирующих на границе сред и при любом угле падения первичной SH-волны при z = 0 проходящая волна  представляет собой простую сумму падающей волны u (τ) и отраженной волны
представляет собой простую сумму падающей волны u (τ) и отраженной волны  .
.
Поэтому все трансформации отраженной волны в закритической зоне входят составной частью в изменения проходящей волны.
Вне зависимости от угла падения в этой волне всегда присутствует “постоянная" составляющая - первичная, падающая на границу волна, по предположению, не меняющаяся с изменением угла падения.
В заключение приведем цифровые оценки особых углов падения  для границы раздела сред со следующими упругими параметрами:
для границы раздела сред со следующими упругими параметрами:
 .
.
Это - довольно “сильная” отражающая граница.
Ей может соответствовать, например, граница между обводненной верхней средой (где скорость S-волны резко уменьшена) и “сухим” нижним полупространством.
При нормальном падении (α = 0) SH-волны коэффициенты рассеивания равны:
 .
.
Отраженная волна имеет амплитуду, в четыре раза меньшую амплитуды первичной волны, и инвертирована по знаку смещения. Проходящая волна ослаблена по амплитуде на четверть в сравнении с падающей волной. Для выбранных параметров сред определим отношения волновых сопротивлений  ≈1,667 и скоростей
≈1,667 и скоростей  ≈1,414 (
≈1,414 ( ≈0,707). Используя их, найдем особые углы падения первичной волны:
≈0,707). Используя их, найдем особые углы падения первичной волны:
угол  , при котором А = 0, В = 1 и
, при котором А = 0, В = 1 и 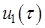 = 0,
= 0, 
 = arcsin
= arcsin  ≈38°,7;
≈38°,7;
критический угол  , при котором А = 1, В = 2 и
, при котором А = 1, В = 2 и

 :
:
 .
.
угол  , при котором ReA = 0, ImA = ImB = ReB = 1 и
, при котором ReA = 0, ImA = ImB = ReB = 1 и
 ,
,  :
:
 ≈49°,4.
≈49°,4.
Как видно из этих оценок, зона наибыстрейшего и наибольшего изменения спектральных коэффициентов рассеивания (СКР) и вторичных волн весьма узка:  ≈10,7. В интервале
≈10,7. В интервале  коэффициенты А и В возрастают на единицу: А от 0 до 1, В от 1 до 2. Затем, как только угол падения превысит критический, коэффициенты становятся комплексными. В интервале
коэффициенты А и В возрастают на единицу: А от 0 до 1, В от 1 до 2. Затем, как только угол падения превысит критический, коэффициенты становятся комплексными. В интервале  действительная часть А спадает от 1 до 0 (ReB от 2 до 1), а мнимая часть А и В возрастает от 0 до 1.
действительная часть А спадает от 1 до 0 (ReB от 2 до 1), а мнимая часть А и В возрастает от 0 до 1.
Вне зоны ( ) коэффициенты рассеивания ведут себя более спокойно. При изменении
) коэффициенты рассеивания ведут себя более спокойно. При изменении  от 0 до
от 0 до  отрицательный коэффициент отражения уменьшается (по модулю) от - 0,25 до 0. В ближней к источнику зоне, при
отрицательный коэффициент отражения уменьшается (по модулю) от - 0,25 до 0. В ближней к источнику зоне, при  , СКР изменяются незначительно. Соответственно, и вторичные волны в этой зоне изменяются мало.
, СКР изменяются незначительно. Соответственно, и вторичные волны в этой зоне изменяются мало.
С увеличением различия свойств контактирующих на границе сред все особые точки ( ) смещаются в сторону меньших углов падения, а интервалы между ними уменьшаются. Наоборот, для границ раздела сред с близкими упругими константами критический угол большой и углы
) смещаются в сторону меньших углов падения, а интервалы между ними уменьшаются. Наоборот, для границ раздела сред с близкими упругими константами критический угол большой и углы  отдалены от него.
отдалены от него.
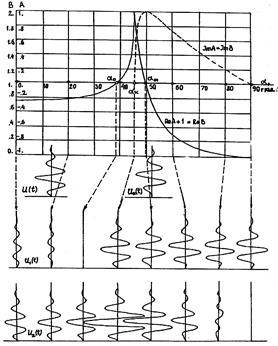
Рис.10
Описание изменений СКР SH-волны иллюстрирует (рис.10), на котором построены графики  и импульсоиды первичной волны и ее Гильберт-трансформанты, а также импульсоиды суммарных вторичных волн
и импульсоиды первичной волны и ее Гильберт-трансформанты, а также импульсоиды суммарных вторичных волн  для различных углов падения. Так как ReB = ReA + 1, график
для различных углов падения. Так как ReB = ReA + 1, график  снабжен второй осью ординат для
снабжен второй осью ординат для  со смещенной на 1 шкалой. График
со смещенной на 1 шкалой. График  одновременно является и графиком
одновременно является и графиком  .
.
Импульсоиды вторичных волн соответствуют углам падения, отмеченным на шкале оси абсцисс стрелками.
В заключение анализа отметим, что угол падения α определяет удаление х точки приема Р от точки возбуждения 0 (рис.11). Тангенс этого угла равен отношению половины удаления х/2 к эхо-глубине границы h: 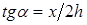 . Поэтому малые углы падения соответствуют ближней к источнику зоне, а большие - дальней.
. Поэтому малые углы падения соответствуют ближней к источнику зоне, а большие - дальней.


Рис.11
Приведем оценки x/h, соответствующие особым углам для выбранных ранее параметров сред:
при  ≈38°,7
≈38°,7 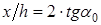 ≈1,6;
≈1,6;
при 
 ;
;
при  ≈49,4
≈49,4  ≈2,33.
≈2,33.
Добавим еще оценку границы ближней зоны:
при  ≈12,8
≈12,8  ≈0,46.
≈0,46.
Таким образом, область наибольшей стабильности отраженной волны не превышает половины эхо-глубины границы. Наибольшие изменения этой волны начинаются на удалениях, в полтора раза превышающих глубину. В промежуточной зоне с ростом х изменения отраженной волны становятся все более существенными и заметными.
II. Расчётная часть
|
|
|


