 |
Тема 5.2 Средние величины в статистике
|
|
|
|
1. Понятие и виды степенных средних величин.
2. Структурные средние величины.
3. Показатели вариации.
Средняя величина – обобщающая характеристика изучаемого признака, отражающая его типичный уровень в расчёте на единицу совокупности в конкретных условиях места и времени.
Средние величины – это общая характеристика совокупности по количественному признаку, показывающему уровень признака, которая относится ко всей совокупности.
Основным условием научного использования средней величины является качественная однородность совокупности. Средние величины являются именованными числами и имеют ту же размерность, что и признак у отдельных единиц совокупности.
Средние величины могут быть:
· общими – рассчитанные по совокупности в целом
· групповыми – исчисленные для каждой группы
Виды средних величин
1. Степенные средние величины
В основе их расчета лежит общая формула: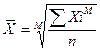 
,
если m = 1 – средняя арифметическая
m = -1 – средняя геометрическая
m = 0 – средняя геометрическая
m = 2 – средняя квадратическая
m = 3 – средняя кубическая
У степенных средних есть свойство возрастать с повышением степени показателя, которое называется правилом мажорантности средних.
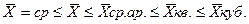
Степенные средние величины могут быть простыми и взвешенными.
2.Структурные средние величины: мода и медиана
К степенным средним относятся:
- Средняя арифметическая – применяется в тех случаях, когда объем варьирующего признака для всей совокупности является сумма значений признаков отдельных ее единиц.
Средняя арифметическая простая
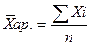
Средняя арифметическая взвешенная
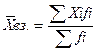
Пример: Вычислить средний стаж 10 работников по данным: 6.5.4.3.3. 4.5.4.5.4.(лет)
|
|
|
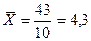лет (простая); 
лет(взвешенная)
Средняя арифметическая обладает некоторыми свойствами:
1.Если значение признака каждой единицы совокупности уменьшить или увеличить на одну и ту же величину А, то со средней произойдут те же изменения.
2.Если значение признака каждой единицы умножить или разделить на постоянное число А, то средняя арифметическая уменьшится или увеличится в А раз.
3.Если частоту каждого значения признака уменьшить или увеличить в n раз, средняя арифметическая не изменится.
- Средняя гармоническая – величина обратная средней арифметической, применяется, когда статистическая информация не содержит частоты по отдельным вариантам совокупности, а представлена, как их произведение, или при расчете общей средней из среднегрупповых.
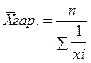- простая 
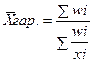- взвешенная,
Где 
- вес средней
Пример: Определить среднюю цену на товар по следующим данным.
Таблица 2 - Цена и сумма реализации на товары по трем городам
| Город | Цена, тыс.руб. (х) | Сумма реализации тыс./руб. (w) | Количество реализованных ед. кг. (f) |
| А | |||
| В | |||
| С | |||
| Итого: |
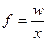
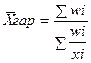
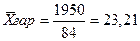тыс. руб.
- Средняя геометрическая - применяется при расчетах средних относительных величин динамики (цепных), т.е. характеризует средний коэффициент роста.
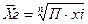- простая 
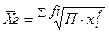- взвешенная
Пример: Темп роста товарооборота по годам составил:
1997г. – 1,053 1999г. – 1,049 1998г. – 1,051 2000г. – 1,058
Определить средний темп роста товарооборота
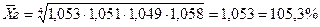
Так же средняя геометрическая может применяться для определения равноудаленной величины от максимального и минимального значения признака.
Пример: Страховая сумма выплат по страховке может изменится от 100 000 до 10 000 руб. в год. Определить среднюю сумму выплат.
руб.
Ответ: Средняя сумма выплат (страховых) в год составляет 1000 рублей.
- Средняя квадратическая – используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической.
|
|
|
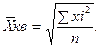- простая 
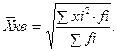- взвешенная
- Средняя кубическая
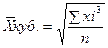- простая 
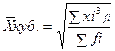- взвешенная
Структурные средние величины применяются для изучения внутреннего строения и структуры рядов распределения значений признака.
К ним относится:
Мода – наиболее часто встречающиеся значение признака, т.е. имеющее наибольшую частоту. В интервальном ряду с равными интервалами, мода вычисляется по формуле. 
,
Где xмо – начало модального интервала, нижняя граница
i – величина модального интервала
fмо – частота в модальном интервале
fмо-1 – частота предмодального интервала
fмо+1 –частота послемодального интервала
Медиана – это вариант, который находится в середины вариационного ряда и делит его на две равные части. Для определения медианы вариационного ряда, необходимо его проранжировать и найти порядковый номер медианы.
Медиана, в интервальных рядах, рассчитывается по формуле
,
Где Xме – начало медианного интервала
Sме-1 – сумма накопленных частот ряда, предшествующего медианному интервалу.
Медианным считается тот интервал, в котором накопленная частота превышает половину суммы всех частот.
3.
Показатели вариации характеризуют колеблемость отдельных значений признака. К ним относится:
Абсолютные показатели
1.1 Размах вариации 
1.2 Среднее линейное отклонение
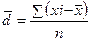для не сгруппированных
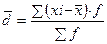для сгруппированных
1.3 Дисперсия – средняя из квадратов отклонений вариантов значений признака от их средней величины
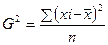для не сгруппированных
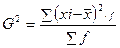для сгруппированных
1.4 Среднее квадратическое отклонение
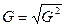
Дисперсия обладает некоторыми свойствами:
- Дисперсия постоянной величины равна нулю
- Если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменяется.
- Если все варианты значения признака уменьшится в К раз, то дисперсия уменьшится К2 раз.
Относительные показатели вариации
2.1 Относительный размах вариации
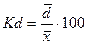
2.2 Коэффициент вариации 
Если коэффициент вариации более 33%, то вариация является неоднородной.
|
|
|
