Подбор подходящего закона распределения вероятностей

Далее рассмотрим некоторые известные распределения, такие как экспоненциальное, нормальное и гамма-распределение, с целью проверки подчиняется ли наше распределение вероятностей заданному.

Проверка на соответствие данных испытаний распределению производится перебором трех распределений, указанных выше, включая заданное, а именно гамма-распределение.

Чтобы иметь полную информацию о распределении случайной величины, надо знать параметры этого распределения. Таким образом, математическое ожидание случайной величины t равно выборочной средней, а среднее квадратическое отклонение случайной величины t – выборочному среднему квадратическому отклонению. Указанные характеристики находятся в ячейках F12 и F14 соответственно. Поместим эти значения в ячейки А2 и В2 соответственно (таблица 5).

Определим параметры экспоненциального (λ), нормального (m – математическое отклонение и σ – среднее квадратическое отклонение) и гамма-распределения (α и β) в соответствии с формулами:

 

, ,

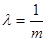B5 = 1/A2;

B8 = A2;

B9 = B2;

B12 = (A2/B2)^2;

B13 = B2^2/A2.

 

Таблица 5 – Значения плотностей распределения

	A	B	C	D	E
1	Матем. ожидание	Ср. кв. отклон.
2	98,68	8,767340682
3
4	Параметры экспоненциального распределения
5	λ	0,0101
6
7	Параметры нормального распределения
8	m	98,6800
9	σ	8,767340682
10
11	Параметры гамма-распределения
12	α	126,6842
13	β	0,7789
14
15	Середина	Плотность относит. частот	Плотность экспоненц. распред.	Плотность нормал. распред.	Плотность гамма- распред.
16	72,5000	0	0,0049	0,0005	0,0003
17	77,5000	0,002	0,0046	0,0025	0,0019
18	82,5000	0,008	0,0044	0,0083	0,0080
19	87,5000	0,032	0,0042	0,0202	0,0213
20	92,5000	0,036	0,0040	0,0355	0,0374
21	97,5000	0,048	0,0038	0,0451	0,0456
22	102,5000	0,032	0,0036	0,0414	0,0399
23	107,5000	0,022	0,0034	0,0274	0,0259
24	112,5000	0,014	0,0032	0,0131	0,0128
25	117,5000	0,006	0,0031	0,0045	0,0049

 

В ячейках В16:В25 вычислим плотности относительных частот как частное от деления относительных частот (ячейки F25:F34) на шаг (ячейка $F$22) из таблицы 4.

Плотности экспоненциального, нормального и гамма-распределений рассчитываются в соответствии с формулами:

С16 = ЭКСПРАСП (А16;$B$5;ЛОЖЬ);

D16 = НОРМРАСП (А16;$B$8;$B$9;ЛОЖЬ);

E16 = ГАММАРАСП (А16;$B$12;$B$13;ЛОЖЬ).

Затем копируем их в блок ячеек С17:Е25.

После чего строим гистограмму частот, совмещенную с плотностью каждого из указанных ранее распределений. Графическое изображение гистограммы кривых различных распределений приведены на рисунках 3- 5.

 

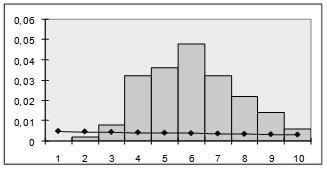
Рисунок 3 – Сглаживание гистограммы плотностью экспоненциального распределения

 

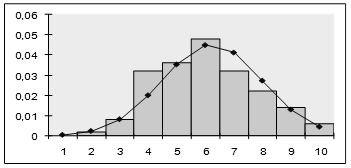
Рисунок 4 – Сглаживание гистограммы плотностью нормального распределения

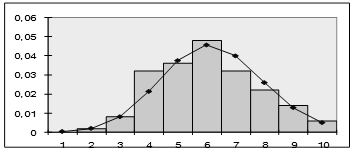
Рисунок 5 – Сглаживание гистограммы плотностью гамма-распределения

 

Используя критерий χ², установим, верна ли принятая гипотеза о том, что статистические данные подчиняются нормальному распределению.

Для применения критерия χ² необходимо, чтобы частоты n_i, соответствующие каждому интервалу, были не меньше 5. Для этого при необходимости объединим рядом стоящие интервалы, а их частоты суммируем. Далее вычислим следующую сумму:

 

,

 

где p_i – теоретическая вероятность того, что случайная величина Х примет значение из интервала [a_i-1,a_i].

Предположим, что случайная величина t имеет функцию распределения F(t), поэтому p_i = F(a_i) – F(a_i-1).

Образец расчетов по предыдущей формуле для трех распределений представлен в таблице 6.

В колонке А содержатся левые, а в колонке В – праве границы интервалов. В колонке С находятся соответствующие частоты. В колонке D рассчитываются теоретические вероятности в зависимости от вида распределения.

Для экспоненциального распределения:

D31 = ЭКСПРАСП (B31; $B$5; ИСТИНА) – ЭКСПРАСП (А31; $B$5; ИСТИНА);

Для нормального распределения:

D40 = НОРМРАСП (В40; $B$8; $B$9; ИСТИНА) – НОРМРАСП (А40; $B$8; $B$9; ИСТИНА);

Для гамма-распределения:

D49 = ГАММАРАСП (В49; $B$12; $B$13; ИСТИНА) – ГАММАРАСП (А49; $B$12; $B$13$ ИСТИНА).

В колонке Е рассчитываются слагаемые соотношения по формуле:

Е31 = (С31-100*В31)^2/(100*D31), которая копируется в другие ячейки колонки Е.

После чего для каждого рассмотренного распределения определим итоговые суммы:

Е38 = СУММ(E34:E39);

Е47 = СУММ(E42:E47);

Е56 = СУММ(Е50:Е55).

Которые равны соответственно 659,6862; 5,2199 и 3,8740.

Гипотеза о виде закона распределения должна быть принята, если вычисленное значение χ²_выч достаточно мало, а именно не превосходит критического значения χ²_кр, которое определяется по распределению χ² в зависимости от заданного уровня значимости α и числа степеней свободы r=k^’ – s – 1. где k^’ – количество интервалов после объединения; s – число неизвестных параметров распределения, которые были определены по выборке.

В данном примере r = 7 – 2 – 1 = 2

Критическое значение рассчитывается по формуле:

Е57 = ХИ2ОБР(0,05;4), из таблицы 6 видно, оно равно 9,4877.

Поскольку 5,2199<9,4877, то принимается гипотеза о том, что статистические данные имеют нормальное распределение с параметрами α = = 98,68и σ = 8,7673 соответственно.

Таблица 6 – Подбор распределения на основе критерия χ²

	А	B	С	D	E
29	Левая граница	Правая граница	Частота	Вероятности	χ²
30				Экспоненциальное распределение
31	70	85	5	0,069374468	0,5411
32	85	90	16	0,020878363	92,7028
33	90	95	18	0,019846835	129,2349
34	95	100	24	0,018866271	259,1934
35	100	105	16	0,017934153	112,5378
36	105	110	11	0,017048088	50,6805
37	110	120	10	0,031610928	14,7957
38	Сумма				659,6862
39				Нормальное распределение
40	70	85	5	0,058804812	0,1318
41	85	90	16	0,101737571	3,3365
42	90	95	18	0,176260064	0,0079
43	95	100	24	0,222500256	0,1376
44	100	105	16	0,204663183	0,9747
45	105	110	11	0,137173828	0,5383
46	110	120	10	0,090811892	0,0930
47	Сумма				5,2199
48				Гамма-распределение
49	70	85	5	0,053672643	0,0251
50	85	90	16	0,107072418	2,6163
51	90	95	18	0,185399233	0,0157
52	95	100	24	0,224931406	0,1009
53	100	105	16	0,197757868	0,7209
54	105	110	11	0,129724735	0,2999
55	110	120	10	0,090713209	0,0951
56	Сумма				3,8740
57	Критическое значение критерия				9,4877

 

1234	Поделиться:

Воспользуйтесь поиском по сайту: