 |
Комментарии к определению клеточного пространства
|
|
|
|
1. Замыкание клетки может не быть клеточным пространством. Пример: разбиение букета 
на клетки 
, 
и (
) - 
делает его клеточным пространством, но если а не есть отмеченная точка окружности 
, то замыкание последней клетки не является подпространством (см. рис.1).
Рис.1
2. Из (W) не следует (С). Разбиение диска D2 на внутренность Int D2 и отдельные точки граничной окружности 
удовлетворяет аксиоме (W) (потому что всегда F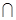 
Int D 2 = F), но не удовлетворяет аксиоме (С).
3. Из (С) не следует (W). Возьмем бесконечное семейство 
│α=1,2,…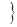 
копий отрезка I, отождествим нулевые концы и топологизируем получившееся множество при помощи метрики: расстояние между точками 
, 
равно 
, если 
, и равно 
, если 
. Разбиение построенного пространства на множества 
и оставшиеся точки не удовлетворяет, из условий, входящих в определение клеточного пространства, только аксиоме (W): точки 
составляют последовательность, сходящуюся к 0, и, значит, незамкнутое множество, но пересечение этой последовательности с замыканием любой клетки замкнуто.
Кстати, если, как это только что было, разбиение пространства на клетки удовлетворяет всем условиям из определения клеточного пространства, кроме аксиомы (W), то можно ослабить в этом пространстве топологию, определив новую топологию при помощи аксиомы (W). Эта процедура называется "клеточным ослаблением топологии".
Клеточные разбиения классических пространств
Сферы и шары
При конечном n имеется два канонических клеточных разбиения сферы 
. Первое состоит из двух клеток: точки 
(любой, скажем, (1,0,......, 0)) и множества 
(рис.2а). Характеристическое отображение 
, отвечающее второй клетке, - это обычное "сворачивание" сферы из шара; годится, например, отображение, действующее по формуле 
, где 
(рис.3).
|
|
|
Рис.2
Рис.3
Другое каноническое клеточное разбиение сферы 
состоит из 2n +2 клеток 
: клетка 
состоит из точек 
, у которых 
и 
(рис.2б). Заботиться о характеристических отображениях здесь не приходится: замыкание каждой клетки очевидным образом гомеоморфно шару соответствующей размерности.
Заметим, что оба описанные клеточные разбиения сферы 
получаются из единственного возможного разбиения сферы 
(двоеточия) посредством применения канонической конструкции клеточного разбиения надстройки: в первом случае нужно брать надстройку над сферой как над пространством с отмеченной точкой, а во втором случае - обыкновенную надстройку.
Существует, конечно, масса других клеточных разбиений сферы : ее можно разбить на 3n+1 - 1 клеток как границу (n+1) - мерного куба, на 
клеток - как границу (n+1) - мерного симплекса и т.п..
Все описанные клеточные разбиения, кроме самого первого, годятся для сферы 
.
Клеточное разбиение шара 
можно получить из любого клеточного разбиения сферы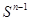 
путем присоединения одной клетки Int с характеристическим отображением id: 
. Наиболее экономное клеточное разбиение шара 
состоит, таким образом, из трех клеток. Правда, ни одно из этих разбиений не годится для шара 
.
Проективные пространства
При отождествлении диаметрально противоположных точек сферы 
клетки 
- клеточного разбиения склеиваются между собой и получается (n+1) - клеточное разбиение пространства R 
, по одной клетке 
в каждой размерности q≤n. Это же разбиение можно описать так:
R │ 
.
Еще одно описание этого разбиения: имеется цепочка включений
R 
R 
R 
R ,
и мы полагаем eq = R 
- R 
. Характеристическим отображением для eq служит композиция канонической проекции Dq R и включения R 
R 
. При n= 
наша конструкция доставляет клеточное разбиение пространства R , содержащее по одной клетке каждой размерности. Конструкция имеет также комплексный, кватернионный и кэлиев аналоги. Она дает: разбиение пространства С на клетки размерностей 0, 2, 4,..., 2n; разбиение пространства H на клетки размерностей 0, 4, 8,..., 4n; разбиение пространства СаР2 на клетки размерностей 0,8,16; клеточные разбиения пространств С 
и H , содержащие по одной клетке в каждой размерности, делящейся, соответственно, на 2 и 4. Например, пространство С разбивается на клетки
|
|
|
С │ 
с характеристическими отображениями
C 
С 
.
Многообразия Грассмана
Описываемое ниже клеточное разбиение многообразий Грассмана очень важно для геометрии и топологии (особенно для теории характеристических классов). Составляющие его клетки называются клетками Шуберта, а само оно называется шубертовским.
Пусть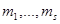 
- произвольная конечная (возможно, пустая) невозрастающая последовательность целых положительных чисел, не превосходящих k, причем s ≤ n - k. Обозначим через e (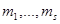) подмножество пространства G (n,k), составленное из подпространств 
пространства R 
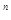, удовлетворяющих следующим условиям (мы полагаем 
=0):
R 
при m ≤ k - m 
;
codim 
(
R ) =о при 
;
R при m ≤ k + s + 1
(мы считаем, что Ra 
R 
при a < b: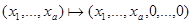 
). Приведем другое, более простое описание множества e (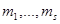). Напомним, что диаграмма Юнга набора 
- это фигура, которая рисуется на клетчатой бумаге, как показано на рис.4а (столбцы имеют длины ).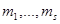
Число клеток диаграммы Юнга равно 
. Можно считать, что клетки пространства G (n,k) отвечают диаграммам Юнга, вмещающимся в прямоугольник k 
(n - k) (рис.4а). Рассмотрим диаграмму Юнга набора и расположим ее, как показано на рис.4б. Толстая линия на этом рисунке представляет собой график некоторой неубывающей функции 
, и множество e (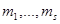) задается условием dim ( R ) = (m). Ввиду наличия такого простого описания, множество e (
) обозначают иногда через е (
), где - обозначение для диаграммы Юнга набора (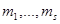). Еще раз заметим, что размерность клетки е (
) равна числу клеток диаграммы .
Лемма. Множество e (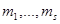) гомеоморфно R 
.
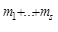Доказательство. Расчленим диаграмму Юнга набора (), как показано на рис.4в. Поставим в клетках вдоль косых линий единицы, в Заштрихованные клетки - произвольные числа и в остальные места - нули. Получится k 
n-матрица, строки которой составляют базис некоторого k-мерного подпространства пространства R 
. Легко понять, что это подпространство принадлежит e () и что всякое подпространство, принадлежащее e (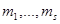), обладает единственным базисом указанного вида. Получаем параметризацию клетки e (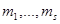) наборами из 
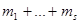чисел (числа в заштрихованных клетках).
|
|
|
Рис.4
На самом деле верно больше: множества e (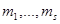) составляют клеточное разбиение пространства G (n, k). Для доказательства нужно построить характеристические отображения, т.е. продолжить построенные гомеоморфизмы Int 
R 
e (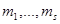
) до непрерывных отображений 
G (n, k), отображающих сферу 
в объединение клеток меньших размерностей.
Замечательное свойство шубертовских клеток состоит в том, что при естественных вложениях G (n, k) в G (n+1, k) ив G (n+1, k+1) клетка e (
) гомеоморфно накладывается на клетку того же наименования. Следовательно, пространство G (
,k) разбивается на клетки Шуберта, отвечающие диаграммам Юнга, содержащимся в горизонтальной полуполосе высоты k, а пространство G (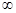
, ) разбивается на клетки, отвечающие всем без исключения диаграммам Юнга. Во всех случаях размерности клеток равны числам клеток диаграмм Юнга.
Комплексные и кватернионные аналоги шубертовских клеток очевидны; разумеется, размерности комплексных и кватернионных аналогов клеток Шуберта соответственно в 2 и 4 раза превосходят числа клеток соответствующих диаграмм Юнга.
Многообразия флагов
Многообразия флагов имеют естественное клеточное разбиение, обобщающее шубертовское разбиение многообразий Грассмана. Это разбиение и его клетки также называются шубертовскими. Опишем разбиение в вещественном случае (комплексный и кватернионный случаи отличаются только удвоением и учетверением размерностей клеток).
Шубертовские клетки многообразия флагов характеризуются наборами размерностей 
пересечений V 
R 
. Числа , однако, должны удовлетворять набору довольно неудобных условий, и мы предпочтем следующее, более рациональное описание клеток Шуберта.
|
|
|
Клетки пространства F (n;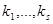 
) отвечают наборам 
целых чисел, принимающих значения 1,…, s + 1, причем ровно 
из этих чисел равны j (j=1,…, s+1; мы считаем, что k 
=0 и k 
=n). Клетка е [ ], отвечающая набору (), состоит из флагов V 
V 
, у которых
dim 
{ 
(мы считаем, что V =0 и V есть все пространство R 
) или, иначе,
dim (V R ) = card {р ≤ i│kp ≤ j }.
Размерность клетки е [ ] равна числу пар (i, j), для которых i<j, 
> 
.
В частности, многообразие F (n; 1,…,n-1) полных флагов разбито на n! клеток, отвечающих обыкновенным перестановкам чисел 1,…, n, причем размерность клетки равна числу инверсий в перестановке.
Если многообразие флагов есть многообразие Грассмана G (n, k), то s = 1 и набор состоит из k единиц и n-k двоек. Построим по этому набору n-звенную ломаную на плоскости, начинающуюся в точке (0, k) и кончающуюся в точке (n-k, 0). Все звенья ломаной имеют длину 1, причем i-e звено направлено вниз, если = 1, и вправо, если 
= 2. Эта ломаная ограничивает (вместе с координатными осями) некоторую диаграмму Юнга 
, и легко понять, что е [ ] = е (
).
Заметим в заключение, что клетки е [ ] (и их комплексные и кватернионные аналоги) могут быть описаны чисто групповым образом: это - орбиты группы нижних треугольных n n-матриц с единицами на диагонали, естественным образом действующей в многообразии флагов. Именно, клетка е [ ] есть орбита флага, i-е пространство которого порождено координатными векторами, номера р которых удовлетворяют неравенству 
< i.
Классические поверхности
Клеточные разбиения поверхностей S2 и RP2 нами уже построены. Клеточные разбиения остальных поверхностей без края автоматически получаются при склеивании этих поверхностей из многоугольников: двумерная клетка получается из
внутренности многоугольника, одномерные клетки - из его (открытых) ребер, нульмерные клетки - из его вершин. Каноническое клеточное разбиение каждой классической поверхности имеет одну двумерную и одну нульмерную клетку. Кроме того, сфера с g ручками имеет 2g одномерных клеток (см. рис.5), проективная плоскость с g ручками имеет 2g +1одномерную клетку и бутылка Клейна с g ручками имеет 2g +2 одномерных клеток.
Рис.5
|
|
|
