 |
Теорема о клеточной аппроксимации
|
|
|
|
Теорема. Всякое непрерывное отображение одного клеточного пространства в другое гомотопно клеточному отображению.
Мы будем доказывать следующее, более сильное утверждение ("относительный вариант" нашей теоремы).
Теорема. Пусть f - непрерывное отображение клеточного пространства X в клеточное пространство Y, причем на клеточном подпространстве А пространства X отображение f клеточно. Тогда существует такое клеточное отображение g: X  Y, что g│A =f│A и, более того, f~g relA.
Y, что g│A =f│A и, более того, f~g relA.
Поясним запись f~g relA (читается: f гомотопно g относительно А), которой мы будем пользоваться и дальше. Она применяется в ситуации, когда непрерывные отображения f, g: X  Y совпадают на подпространстве А пространства X и означает, что существует гомотопия h
Y совпадают на подпространстве А пространства X и означает, что существует гомотопия h  : Х
: Х  Y, соединяющая f с g и неподвижная на А, т.е. такая, что ht (а) не зависит от t при а
Y, соединяющая f с g и неподвижная на А, т.е. такая, что ht (а) не зависит от t при а 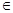 А. Конечно, из f~ g relА следует, что f ~ g, но не наоборот. Пример: f,g: I
А. Конечно, из f~ g relА следует, что f ~ g, но не наоборот. Пример: f,g: I  S
S 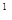 , f - "наворачивание" отрезка на окружность, g - отображение в точку; эти отображения гомотопны, но не гомотопны rel (0
, f - "наворачивание" отрезка на окружность, g - отображение в точку; эти отображения гомотопны, но не гомотопны rel (0 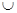 1).
1).
Доказательство теоремы. Предположим, что отображение f уже сделано клеточным не только на всех клетках из А, но и на всех клетках из X, имеющих размерность < р. Возьмем р-мерную клетку ер 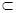 X - А. Ее образ f (ep) пересекается лишь с конечным числом клеток пространства Y (это следует из компактности f (
X - А. Ее образ f (ep) пересекается лишь с конечным числом клеток пространства Y (это следует из компактности f (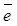 p)). Выберем среди этих клеток пространства Y клетку наибольшей размерности, скажем,
p)). Выберем среди этих клеток пространства Y клетку наибольшей размерности, скажем, 
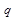 , dim
, dim 
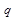 = q. Если q≤ р, то нам с клеткой ер делать нечего. В случае же q >р нам потребуется следующая лемма.
= q. Если q≤ р, то нам с клеткой ер делать нечего. В случае же q >р нам потребуется следующая лемма.
Лемма о свободной точке. Пусть U - открытое подмножество пространства Rp и 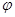 : U
: U 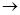 IntDq - такое непрерывное отображение, что множество V =
IntDq - такое непрерывное отображение, что множество V = 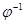 (dq)
(dq)  U, где dq - некоторый замкнутый шарик в IntD
U, где dq - некоторый замкнутый шарик в IntD  , компактно. Если q> р, то существует непрерывное отображение
, компактно. Если q> р, то существует непрерывное отображение  : U
: U 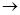 Int Dq, совпадающее с
Int Dq, совпадающее с 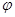 вне
вне
|
|
|
V и такое, что его образ не покрывает всего шара dq.
Доказательство этой леммы (и обсуждение ее геометрического значения) мы отложим до следующего пункта; ограничимся лишь важным замечанием, что отображение  автоматически будет гомотопным
автоматически будет гомотопным 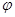 относительно U - V: достаточно взять связывающую
относительно U - V: достаточно взять связывающую 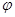 с
с  "прямолинейную" гомотопию, при которой точка
"прямолинейную" гомотопию, при которой точка 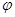 (u) равномерно движется к
(u) равномерно движется к  (u) точке по прямолинейному отрезку, соединяющему
(u) точке по прямолинейному отрезку, соединяющему 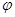 (u) с
(u) с  (u).
(u).
Завершим доказательство теоремы. Из леммы о свободной точке вытекает, что сужение f│ 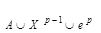 гомотопно rel (A
гомотопно rel (A 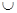 X
X 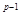 ) отображению f’: A
) отображению f’: A 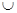 X
X 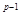
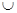 е р
е р 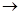 Y, такому, что f’ (ep) задевает те же клетки, что и f (e р), но заведомо f’ (ep) не содержит всю клетку
Y, такому, что f’ (ep) задевает те же клетки, что и f (e р), но заведомо f’ (ep) не содержит всю клетку 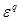 . В самом деле, пусть h: Dp
. В самом деле, пусть h: Dp 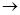 Х, k: Dp
Х, k: Dp 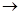 Y - характеристические отображения, соответствующие клеткам ер,
Y - характеристические отображения, соответствующие клеткам ер, 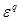 . Положим U=
. Положим U= 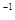 h (f
h (f 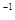 (
( )
)  ер) и определим отображение
ер) и определим отображение 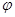 : U
: U 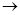 Int Dq как композицию:
Int Dq как композицию:
u 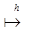 x
x 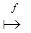 y
y 
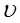 =
= 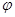 (u)
(u)
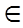
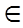
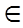
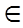
U e 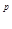
 f
f  (
(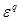 )
) 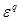 Int Dq Обозначим через dq (замкнутый) концентрический подшар шара Dq. Множество V=
Int Dq Обозначим через dq (замкнутый) концентрический подшар шара Dq. Множество V= 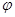
 (dq) компактно (как замкнутое подмножество шара Dp). Пусть
(dq) компактно (как замкнутое подмножество шара Dp). Пусть  : U
: U 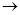 IntDq - отображение, доставляемое леммой о свободной точке. Отображение f' определим как совпадающее с f вне h (U) и как композицию
IntDq - отображение, доставляемое леммой о свободной точке. Отображение f' определим как совпадающее с f вне h (U) и как композицию
x 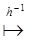 u
u 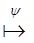
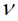
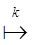 y = f’ (x)
y = f’ (x)
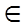
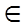
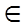
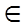
h (U) U Int Dq 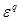
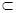 Y
Y
на h (U). Ясно, что отображение f’ непрерывно (оно совпадает с f на "буферном множестве" h (U - V)) и гомотопно f│ 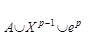 rel (A
rel (A 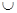 X
X 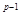 ), и даже rel (A
), и даже rel (A 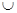 X
X 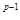
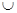 (e
(e 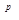 -h (V)))) (это вытекает из гомотопности
-h (V)))) (это вытекает из гомотопности 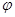 ~
~  rel (U - V)). Ясно также, что f' (ep) не покрывает eq.
rel (U - V)). Ясно также, что f' (ep) не покрывает eq.
Дальнейшее рассуждение совсем просто. Во-первых, неподвижную на A 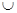 Х
Х 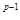 гомотопию между f│
гомотопию между f│ 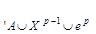 и f' мы можем распространить, по теореме Борсука, на все X, и это позволяет считать, что отображение f', обладающее всеми вышеперечисленными свойствами, определено на всем X. После этого мы берем точку у0
и f' мы можем распространить, по теореме Борсука, на все X, и это позволяет считать, что отображение f', обладающее всеми вышеперечисленными свойствами, определено на всем X. После этого мы берем точку у0 
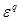 , не принадлежащую f’ (ер), и подвергаем f'│
, не принадлежащую f’ (ер), и подвергаем f'│ 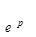 "радиальной гомотопии": если точка x
"радиальной гомотопии": если точка x  ep не принадлежит f’
ep не принадлежит f’ 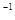 (
(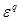 ),To f' (x) стоит на месте, а если f' (x)
),To f' (x) стоит на месте, а если f' (x) 
 , то f’ (x) движется по отрезку, идущему из точки у0 на границу клетки
, то f’ (x) движется по отрезку, идущему из точки у0 на границу клетки  (точнее говоря, по k-образу прямолинейного отрезка, начинающегося в точке k
(точнее говоря, по k-образу прямолинейного отрезка, начинающегося в точке k 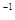 (у0) проходящего через точку k
(у0) проходящего через точку k 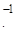 (f’ (x))
(f’ (x)) 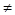 k
k 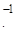 (у0) и кончающегося на граничной сфере S
(у0) и кончающегося на граничной сфере S 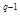 шара Dq). Эту гомотопию мы продолжаем до гомотопии отображения f'│
шара Dq). Эту гомотопию мы продолжаем до гомотопии отображения f'│ 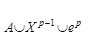 (неподвижной вне ер) и - по теореме Борсука - до гомотопии всего отображения f’: Х
(неподвижной вне ер) и - по теореме Борсука - до гомотопии всего отображения f’: Х 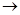 Y. Получающееся отображение f’’ гомотопно f ге1 (A
Y. Получающееся отображение f’’ гомотопно f ге1 (A 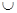 Х
Х 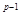 ) и обладает тем свойством, что f’’ (ep) задевает q-мерных клеток на одну меньше, чем f (е р) (и, как и f (ep), не задевает клеток размерности >q). Применив эту процедуру нужное число раз, мы прогомотопируем отображение f к отображению, клеточному на A
) и обладает тем свойством, что f’’ (ep) задевает q-мерных клеток на одну меньше, чем f (е р) (и, как и f (ep), не задевает клеток размерности >q). Применив эту процедуру нужное число раз, мы прогомотопируем отображение f к отображению, клеточному на A 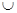 Х
Х 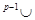 ep, причем гомотопия будет неподвижной на A
ep, причем гомотопия будет неподвижной на A 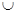 Х
Х 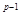 .
.
|
|
|
Теперь заметим, что "исправление" отображения f, которое мы проделали для клетки ер, можно дословно так же проделать одновременно для всех р-мерных клеток из X - А. Тогда мы придем к отображению, клеточному на A 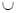 Хр и гомотопному f rel (A
Хр и гомотопному f rel (A 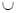 Х
Х 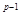 ).
).
Неподвижную на А гомотопию, связывающую отображение f с клеточным отображением, мы получим, если проделаем последовательно построенные гомотопии при р = 0, 1,2,... Правда, число этих гомотопии может быть бесконечно, но это не беда: р-ю гомотопию мы производим на отрезке 1 - 2 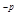 ≤t≤ 1 - 2
≤t≤ 1 - 2 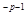 . Непрерывность всей гомотопии обеспечивается аксиомой (W): для каждой клетки е из X гомотопия будет неподвижной, начиная с некоторого te < 1. Теорема доказана.
. Непрерывность всей гомотопии обеспечивается аксиомой (W): для каждой клетки е из X гомотопия будет неподвижной, начиная с некоторого te < 1. Теорема доказана.
|
|
|


