 |
Доказательство леммы о свободной точке
|
|
|
|
Для человека, не испорченного популярной математической литературой, сама формулировка леммы показалась бы нелепой: как же непрерывный образ пространства меньшей размерности может покрыть пространство большей размерности? Но кто же не знает, что это бывает: кривая Пеано, распропагандированная ничуть не меньше, чем, скажем, бутылка Клейна, осуществляет непрерывное (и даже взаимно однозначное) отображение отрезка на квадрат. Поэтому лемму приходится доказывать, и дело осложняется тем, что геометрическая интуиция помочь тут не может, она упорно твердит свое: такое вообще невозможно. С подобными трудностями сталкиваются всякий раз, когда "строгое" определение того или иного понятия (в данном случае  -
- 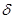 -определение непрерывности) не вполне соответствует исходному интуитивному представлению: приходится вникать в устройство не реального объекта, а химеры. Но ничего не поделаешь - доказать лемму надо.
-определение непрерывности) не вполне соответствует исходному интуитивному представлению: приходится вникать в устройство не реального объекта, а химеры. Но ничего не поделаешь - доказать лемму надо.
В основе второго доказательства леммы лежит понятие триангуляции. Напомним, что q-мерный евклидов симплекс есть подмножество пространства R  , n ≤ q, являющееся выпуклой оболочкой q + 1 точек, не лежащих в одной (q - 1) - мерной плоскости. (Евклидовы симплексы размерностей 0, 1, 2, 3: точка, отрезок, треугольник, тетраэдр.) Эти q+ 1 точек называются вершинами симплекса. Подсимплексы, т.е. выпуклые оболочки различных подмножеств множества вершин, называются гранями нашего симплекса; это - симплексы размерности ≤q. Нульмерная грань - это вершина. Замечательное свойство симплекса заключается в том, что его линейное отображение в любое пространство Rm определяется своими значениями на вершинах, причем эти значения могут быть совершенно произвольны. Конечная триангуляция подмножества евклидова пространства - это такое его конечное покрытие евклидовыми симплексами, что любые два симплекса либо не пересекаются вовсе, либо пересекаются по целой грани. Удобно считать, что грани симплексов триангуляции также принадлежат к числу симплексов триангуляции.
, n ≤ q, являющееся выпуклой оболочкой q + 1 точек, не лежащих в одной (q - 1) - мерной плоскости. (Евклидовы симплексы размерностей 0, 1, 2, 3: точка, отрезок, треугольник, тетраэдр.) Эти q+ 1 точек называются вершинами симплекса. Подсимплексы, т.е. выпуклые оболочки различных подмножеств множества вершин, называются гранями нашего симплекса; это - симплексы размерности ≤q. Нульмерная грань - это вершина. Замечательное свойство симплекса заключается в том, что его линейное отображение в любое пространство Rm определяется своими значениями на вершинах, причем эти значения могут быть совершенно произвольны. Конечная триангуляция подмножества евклидова пространства - это такое его конечное покрытие евклидовыми симплексами, что любые два симплекса либо не пересекаются вовсе, либо пересекаются по целой грани. Удобно считать, что грани симплексов триангуляции также принадлежат к числу симплексов триангуляции.
|
|
|
Барицентрическое подразделение q-мерного симплекса состоит в том, что этот симплекс разбивается на (q + 1)! более мелких q-мерных симплексов. Вершины новых симплексов - это центры тяжести граней старого симплекса (в том числе - его самого). Множество {х0, х  ,..., xq) этих центров является множеством вершин некоторого симплекса барицентрического подразделения, если соответствующие грани
,..., xq) этих центров является множеством вершин некоторого симплекса барицентрического подразделения, если соответствующие грани  0,
0,  ,...,
,...,  q можно составить в цепочку последовательно вложенных друг в друга, см. рис.7. (По-другому барицентрическое подразделение q-мерного симплекса
q можно составить в цепочку последовательно вложенных друг в друга, см. рис.7. (По-другому барицентрическое подразделение q-мерного симплекса  можно описать так: сначала подвергаются барицентрическому подразделению все его (q - 1) - мерные грани, а потом над всеми построенными симплексами, лежащими на границе симплекса
можно описать так: сначала подвергаются барицентрическому подразделению все его (q - 1) - мерные грани, а потом над всеми построенными симплексами, лежащими на границе симплекса  , строятся конусы с вершиной в центре этого симплекса; начать это индуктивное определение можно с q = 0: с нульмерным симплексом при барицентрическом подразделении ничего не происходит. Еще по-другому: симплекс
, строятся конусы с вершиной в центре этого симплекса; начать это индуктивное определение можно с q = 0: с нульмерным симплексом при барицентрическом подразделении ничего не происходит. Еще по-другому: симплекс  - его совокупность точек вида
- его совокупность точек вида  , где
, где 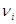 - вершины, t
- вершины, t  ≥ 0 и
≥ 0 и  t
t  = 1; симплексы барицентрического подразделения отвечают перестановкам (i0, i
= 1; симплексы барицентрического подразделения отвечают перестановкам (i0, i  ,..., iq) чисел 0, 1,..., q; симплекс, отвечающий этой перестановке, состоит из точек
,..., iq) чисел 0, 1,..., q; симплекс, отвечающий этой перестановке, состоит из точек
 t
t 
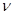 с
с  .
.
Барицентрическое подразделение триангуляции - это триангуляция, составленная из симплексов барицентрических подразделений симплексов исходной триангуляции (рис.8).
Обратимся теперь к нашему отображению  . Прежде всего мы построим в шарике d = dq концентрические шарики d
. Прежде всего мы построим в шарике d = dq концентрические шарики d  , d2, d3, d
, d2, d3, d 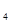 радиусов
радиусов  /5, 2
/5, 2  /5, З
/5, З  /5,4
/5,4  /5, где
/5, где  -радиус шарика d. Далее, покроем V конечным числом р-мерных симплексов, содержащихся в U, и триангулируем объединение К этих симплексов (объединение конечного числа как угодно пересекающихся евклидовых симплексов в Rp обладает конечной триангуляцией). Применив к этой триангуляции достаточное число
-радиус шарика d. Далее, покроем V конечным числом р-мерных симплексов, содержащихся в U, и триангулируем объединение К этих симплексов (объединение конечного числа как угодно пересекающихся евклидовых симплексов в Rp обладает конечной триангуляцией). Применив к этой триангуляции достаточное число
|
|
|

Рис.7 Рис.8
раз барицентрическое подразделение, мы можем добиться того, чтобы для любого симплекса  триангуляции выполнялось неравенство diam
триангуляции выполнялось неравенство diam  (
( ) <
) <  /5. Пусть K1 - объединение симплексов построенной триангуляции нашего множества К,
/5. Пусть K1 - объединение симплексов построенной триангуляции нашего множества К,  -образы которых пересекаются с d4. Тогда d4
-образы которых пересекаются с d4. Тогда d4 
 < (U)
< (U) 
 (K1)
(K1)  d. Рассмотрим отображение
d. Рассмотрим отображение  ': К1
': К1  d, совпадающее с
d, совпадающее с  на вершинах триангуляции и линейное на каждом симплексе. Отображения
на вершинах триангуляции и линейное на каждом симплексе. Отображения  │K
│K  и
и  ’ гомотопны - они соединяются прямолинейной гомотопией
’ гомотопны - они соединяются прямолинейной гомотопией  t: K1
t: K1 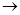 d,
d,  0=
0=  │K,
│K,  1 =
1 =  ’. Теперь "сошьем" отображения
’. Теперь "сошьем" отображения  и
и  ’ в отображение
’ в отображение  : U
: U 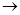 IntDq:
IntDq:
 (u), если
(u), если  (u)
(u)  d3,
d3,  (u) =
(u) =  ’ (u), если
’ (u), если  (u)
(u)  d2,
d2,  3-5
3-5  (u) (u), если
(u) (u), если  (u)
(u)  d3-d2.
d3-d2.
Здесь  (u) - расстояние от точки
(u) - расстояние от точки  (u) до центра шара d. (См. рис.9)
(u) до центра шара d. (См. рис.9)

Рис.9
Отображение  непрерывно, совпадает с
непрерывно, совпадает с  на U - V и его образ пересекается с d1 по конечному числу кусков р-мерных плоскостей, т.е. всего шара d1 (а значит, и всего шара d) не покрывает.
на U - V и его образ пересекается с d1 по конечному числу кусков р-мерных плоскостей, т.е. всего шара d1 (а значит, и всего шара d) не покрывает.
Лемма доказана.
|
|
|


