 |
Свойства статистических оценок
|
|
|
|
Элементы теории оценок неизвестных параметров
Оценки неизвестных параметров
Понятие оценки параметров
Пусть изучается случайная величина X с законом распределения, зависящим от одного или нескольких параметров. Например, это параметр а в распределении Пуассона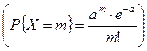 
или параметры а и σ для нормального закона распределения.
Требуется по выборке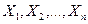 
, полученной в результате n наблюдений (опытов), оценить неизвестный параметр 
.
Напомним, что 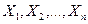- случайные величины: Х 1 - результат первого наблюдения, X 2 - второго и т.д., причем случайные величины 
, 
, имеют такое же распределение, что и случайная величина X. Конкретная выборка 
- это значения (реализация) независимых случайных величин 
.
Статистической оценкой 
(просто оценкой 
) параметра теоретического распределения называют его приближенное значение, зависящее от данных выбора.
Очевидно, что оценка есть значение некоторой функции результатов наблюдений над случайной величиной, т.е.
 .
| (9.1) |
Функцию результатов наблюдений (т.е. функцию выборки) называют статистикой.
Можно сказать, что оценка параметра есть статистика, которая в определенном смысле близка к истинному значению .
Так, 
есть оценка 
, гистограмма - плотности 
.
Оценка является случайной величиной, так как является функцией независимых случайных величин . Если произвести другую выборку, то функция примет другое значение.
Если число опытов (наблюдений) невелико, то замена неизвестного параметра его оценкой , например математического ожидания средним арифметическим, приводит к ошибке. Это ошибка в среднем тем больше, чем меньше число опытов.
К оценке любого параметра предъявляется ряд требований, которым она должна удовлетворять, чтобы быть «близкой» к истинному значению параметра, т.е. быть в каком-то смысле «доброкачественной» оценкой.
|
|
|
Свойства статистических оценок
Качество оценки определяют, проверяя, обладает ли она свойствами несмещенности, состоятельности, эффективности.
Оценка параметра называется несмещенной, если 
. Если 
, то оценка называется смещенной.
Чтобы оценка не давала систематической ошибки (ошибки одного знака) в сторону завышения (
) или занижения (
), надо потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру.
Если 
, то оценка называется асимптотически несмещенной.
Требование несмещенности особенно важно при малом числе наблюдений (опытов).
Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру:
,
т.е. для любого 
выполнено
.
Это означает, что с увеличением объема выборки мы все ближе приближаемся к истинному значению параметра , т.е. практически достоверно 
.
Свойство состоятельности обязательно для любого правила оценивания (несостоятельные оценки не используются).
Состоятельность оценки может быть установлена с помощью следующей теоремы.
Теорема 9.1. Если оценка параметра является несмещенной и 
при 
, то - состоятельная оценка.
Доказательство. Запишем неравенство Чебышева для случайной величины для любого :
.
Так как по условию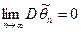 
, то 
. Но вероятность любого события не превышает 1 и, следовательно,
,
т. е. - состоятельная оценка параметра .
Несмещенная оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра , т.е. оценка эффективна, если ее дисперсия минимальна.
Эффективную оценку в ряде случаев можно найти, используя неравенство Рао-Крамера:
,
где 
- информация Фишера, определяющаяся формулой
|
|
|
- для дискретных величин:
,
где 
,
- для непрерывных величин:
,
где 
- плотность распределения непрерывной случайной величины X.
Эффективность оценки определяется отношением
,
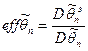где 
— эффективная оценка. Чем ближе 
к 1, тем эффективнее оценка . Если 
при , то оценка называется асимптотически эффективной.
Отметим, что на практике не всегда удается удовлетворить всем перечисленным выше требованиям (несмещенность, состоятельность, эффективность), и поэтому приходится довольствоваться оценками, не обладающими сразу всеми тремя свойствами. Все же три свойства, как правило, выделяют оценку однозначно.
|
|
|
