 |
Точечные оценки математического ожидания и дисперсии
|
|
|
|
Пусть изучается случайная величина X с математическим ожиданием 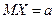 и дисперсией DX, причем оба параметра неизвестны.
и дисперсией DX, причем оба параметра неизвестны.
Статистика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется ее точечной оценкой. То есть точечная оценка характеристики генеральной совокупности - это число, определяемое по выборке.
Пусть  - выборка, полученная в результате проведения n независимых наблюдений за случайной величиной X. Чтобы подчеркнуть случайный характер величин
- выборка, полученная в результате проведения n независимых наблюдений за случайной величиной X. Чтобы подчеркнуть случайный характер величин  , перепишем их в виде
, перепишем их в виде  , т.е. под
, т.е. под  будем понимать значение случайной величины Х i- м опыте. Случайные величины
будем понимать значение случайной величины Х i- м опыте. Случайные величины  можно рассматривать как n независимых компонент величины X. Поэтому
можно рассматривать как n независимых компонент величины X. Поэтому 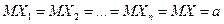 ,
,  .
.
Теорема 9.2. Пусть  - выборка из генеральной совокупности и
- выборка из генеральной совокупности и  ,
,  ,
, 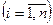 . Тогда выборочное среднее
. Тогда выборочное среднее  - несмещенная и состоятельная оценка математического ожидания MX.
- несмещенная и состоятельная оценка математического ожидания MX.
Доказательство. Найдем математическое ожидание оценки  :
:
 .
.
Отсюда по определению получаем, что  - несмещенная оценка MX. Далее, согласно теореме Чебышева, для любого
- несмещенная оценка MX. Далее, согласно теореме Чебышева, для любого  имеет место равенство
имеет место равенство 
 ,
,
которое, согласно условию теоремы, можно переписать так:

или, что то же самое,  . Согласно определению получаем, что
. Согласно определению получаем, что  - состоятельная оценка MX.
- состоятельная оценка MX.
Можно показать, что при нормальном распределении случайной величины X эта оценка, т.е.  , будет и эффективной. На практике во всех случаях в качестве оценки математического ожидания используется среднее арифметическое, т.е.
, будет и эффективной. На практике во всех случаях в качестве оценки математического ожидания используется среднее арифметическое, т.е.  .
.
В статистике оценку математического ожидания принято обозначать через  или
или  , а не
, а не  .
.
Имеет место равенство (вывод равенства мы опускаем)
 . .
| (9.2) |
Из равенства (9.2) следует, что  , т.е. выборочная дисперсия является смещенной оценкой дисперсии DX. Поэтому выборочную дисперсию исправляют, умножив ее на
, т.е. выборочная дисперсия является смещенной оценкой дисперсии DX. Поэтому выборочную дисперсию исправляют, умножив ее на  , получая формулу
, получая формулу 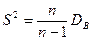 .
.
|
|
|
Теорема 9.3. Пусть  - выборка из генеральной совокупности и
- выборка из генеральной совокупности и  ,
, 
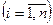 . Тогда исправленная выборочная дисперсия
. Тогда исправленная выборочная дисперсия 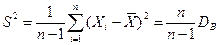 - несмещенная состоятельная оценка дисперсии DX.
- несмещенная состоятельная оценка дисперсии DX.
Примем без доказательства состоятельность оценки 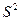 . Докажем ее несмещенность.
. Докажем ее несмещенность.
Доказательство. Имеем
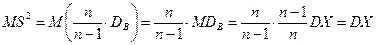 ,
,
т.е. 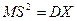 . Отсюда по определению получаем, что
. Отсюда по определению получаем, что 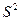 - несмещенная оценка DX.
- несмещенная оценка DX.
Отметим, что при больших значениях n разница между 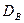 и
и 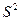 очень мала и они практически равны, поэтому оценку
очень мала и они практически равны, поэтому оценку 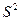 используют для оценки дисперсии при малых выборках, обычно при n ≤ 30.
используют для оценки дисперсии при малых выборках, обычно при n ≤ 30.
Теорема 9.4. Относительная частота 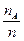 появления события А в n независимых испытаниях является несмещенной состоятельной и эффективной оценкой неизвестной вероятности
появления события А в n независимых испытаниях является несмещенной состоятельной и эффективной оценкой неизвестной вероятности  этого события (р - вероятность наступления события А в каждом испытании).
этого события (р - вероятность наступления события А в каждом испытании).
Отметим, что состоятельность оценки  непосредственно вытекает из теоремы Бернулли.
непосредственно вытекает из теоремы Бернулли.
Теорема 9.5. Эмпирическая функция распределения выборки  является несмещенной состоятельной оценкой функции распределения
является несмещенной состоятельной оценкой функции распределения  случайной величины X.
случайной величины X.
Пример 9.1. Монету подбрасывают n раз. Вероятность выпадения герба при каждом подбрасывания равна  . В ходе опыта монета выпала гербом
. В ходе опыта монета выпала гербом  раз. Показать несмещенность оценки
раз. Показать несмещенность оценки  вероятности
вероятности  выпадения герба в каждом опыте.
выпадения герба в каждом опыте.
Решение:
Число успехов ( ) имеет распределение Бернулли. Тогда
) имеет распределение Бернулли. Тогда 
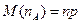 ,
,  .
.
Следовательно,
 ,
,
т.е. оценка  - несмещенная.
- несмещенная.
Методы нахождения точечных оценок
Рассмотрим наиболее распространенные методы получения точечных оценок параметров распределения: метод моментов, метод максимального правдоподобия и метод наименьших квадратов.
Метод моментов
Метод моментов для нахождения точечных оценок неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов распределения соответствующим эмпирическим моментам, найденных по выборке.
|
|
|
Так, если распределение зависит от одного параметра  (например, задан вид плотности распределения
(например, задан вид плотности распределения  ), то для нахождения его оценки надо решить относительно
), то для нахождения его оценки надо решить относительно  одно уравнение:
одно уравнение:
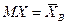
 - есть функция от
- есть функция от  .
.
Если распределение зависит от двух параметров (например, вид плотности распределения 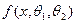 ) - надо решить относительно
) - надо решить относительно  и
и 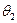 систему уравнений:
систему уравнений:

И, наконец, если надо оценить n параметров 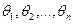 - надо решить одну из систем вида:
- надо решить одну из систем вида:
 или
или 
Метод моментов является наиболее простым методом оценки параметров. Он был предложен в 1894 г. Пирсоном. Оценки метода моментов обычно состоятельны, однако их эффективность часто значительно меньше единицы.
Пример 9.2. Найти оценки параметров нормального распределения случайной величины X методом моментов.
Решение:
Требуется по выборке  найти точечные оценки неизвестных параметров
найти точечные оценки неизвестных параметров  и
и  .
.
По методу моментов приравниваем их, соответственно, к выборочному среднему и выборочной дисперсии ( - начальный момент I порядка,
- начальный момент I порядка,  - центральный момент II порядка). Получаем
- центральный момент II порядка). Получаем
 т.е.
т.е. 
Итак, искомые оценки параметров нормального распределения:
 и
и  .
.
|
|
|


