 |
Понятие интервального оценивания параметров
|
|
|
|
Точечные оценки неизвестного параметра 
хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно, с какой точностью они дают оцениваемый параметр.
Для выборок небольшого объема вопрос о точности оценок очень существенен, так как между и 
может быть большое расхождение в этом случае. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра не одним числом, а целым интервалом 
.
Оценка неизвестного параметра называется интервальной, если она определяется двумя числами - концами интервала.
Задачу интервального оценивания можно сфор£мулировать так: по данным выборки построить числовой интервал , относительно которого с заранее выбранной вероятностью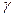 
можно сказать, что внутри этого интервала находится точное значение оцениваемого параметра (рис. 9.1).
Рис. 9.1.
Интервал , накрывающий с вероятностью 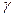истинное значение параметра , называется доверительным интервалом, а вероятность 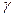- надежностью оценки или доверительной вероятностью.
Очень часто доверительный интервал выбирается симметричным относительно несмещенной точечной оценки , т.е. выбирается интервал вида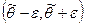 
такой, что
Число 
характеризует точность оценки: чем меньше разность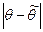 
, тем точнее оценка.
Величина 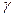выбирается заранее, ее выбор зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, лампочки, игрушки... Надежность 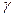принято выбирать равной 0,9; 0,95; 0,99 или 0,999. Тогда практически достоверно нахождение параметра в доверительном интервале .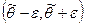
|
|
|
Доверительные интервалы для параметров нормального распределения
Построим доверительные интервалы для параметров нормального распределения, т.е. когда выборка производится из генеральной совокупности, имеющей нормальное распределение с параметрами а и σ2.
Доверительный интервал для математического ожидания при известной дисперсии
Пусть случайная величина 
; σ - известна и доверительная вероятность (надежность) 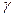- задана.
Пусть 
- выборка, полученная в результате проведения n независимых наблюдений за случайной величиной X. Чтобы подчеркнуть случайный характер величин , перепишем их в виде 
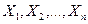, т.е. под 
будем понимать значение случайной величины X в i- м опыте. Случайные величины 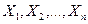- независимы, закон распределения любой из них совпадает с законом распределения случайной величины X (т.е. 
). А это значит, что
,
.
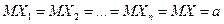Выборочное среднее
также будет распределено по нормальному закону (примем без доказательства). Параметры распределения 
таковы: 
, 
.
Действительно,
,
.
Таким образом,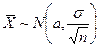 
.
Следовательно, пользуясь формулой
можно записать
,
где 
. Из последнего равенства находим
, (9.3)
поэтому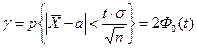 
или
. (9.4)
В соответствии с определением доверительного интервала получаем, что доверительный интервал для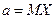 
есть
, (9.5)
где t определяется из равенства (9.4), т.е. из уравнения
(9.6)
или
).
При заданном 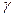по таблице функции Лапласа находим аргумент t.
Заметим, что из равенства (9.3) следует: с возрастанием объема выборки n число ε убывает и, значит, точность оценки увеличивается. Увеличение надежности 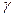влечет уменьшение точности оценки.
Пример 9.5. Произведено 5 независимых наблюдений над случайной величиной 
. Результаты наблюдений таковы: 
, 
, 
, 
, 
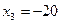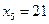. Найти оценку для 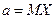, а также построить для него 95%-й доверительный интервал.
Решение:
Находим сначала 
:
, т.е. 
.
|
|
|
Учитывая, что 
и 
, получаем 
.
По таблице выясняем, что 
.
Тогда 
.
Согласно (9.6) доверительный интервал для 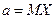таков:
, т.е. (- 13,5; 21,5).
|
|
|
