 |
Выбор факторных признаков для построения регрессионной модели на основе анализа матрицы коэффициентов корреляции.
|
|
|
|
Для построения матрицы парной корреляции всех переменных с помощью пакета SPSS необходимо выполнить следующие действия:
1. Выбрать в верхней строке меню Анализ – Корреляция – Парные.
2. Переменные, относительно которых проверяется степень корреляционной связи, поочередно переместить в поле тестируемых переменных справа (Рис.2.1-.2.2).
3. Начать расчет путем нажатия ОК.

Рис.2.1.

Рис. 2.1 - 2.2. Построение матрицы парной корреляции в SPSS.
В результате в выходной области появиться матрица парной корреляции всех переменных (Таблица 2.1). Полученные результаты содержат: коэффициент корреляции Пирсона, вероятность ошибки, соответствующая предположению о ненулевой корреляции, и количество использованных пар значений n=16.
Коэффициент корреляции R между двумя переменными указывает на силу связи между ними и принимает значения между -1 и +1. При этом, если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой.
Таблица 2.1. Корреляции
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов | |||
| Объем реализации | Корреляция Пирсона | .678(**) | .646(**) | .233 | .226 | .816(**) | ||
| Знч.(2-сторон) | .004 | .007 | .385 | .399 | .000 | |||
| N | ||||||||
| Время | Корреляция Пирсона | .678(**) | .106 | .174 | -.051 | .960(**) | ||
| Знч.(2-сторон) | .004 | .695 | .520 | .851 | .000 | |||
| N | ||||||||
| Реклама | Корреляция Пирсона | .646(**) | .106 | -.003 | .204 | .273 | ||
| Знч.(2-сторон) | .007 | .695 | .990 | .448 | .306 | |||
| N | ||||||||
| Цена | Корреляция Пирсона | .233 | .174 | -.003 | .698(**) | .235 | ||
| Знч.(2-сторон) | .385 | .520 | .990 | .003 | .380 | |||
| N | ||||||||
| Цена конкурента | Корреляция Пирсона | .226 | -.051 | .204 | .698(**) | .031 | ||
| Знч.(2-сторон) |
|
|
|
** Корреляция значима на уровне 0.01 (2-сторон.).
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем реализации имеет тесную связь с индексом потребительских расходов (ryx5= 0.816), с расходами на рекламу (ryx2 = 0.646) и со временем (ryx1 = 0.678). Однако факторы Х2 и Х5 тесно связаны между собой (rх 1x5 = 0.96), что свидетельствует о наличии мультиколлинеарности. Из этих двух переменных оставим в модели Х5 - индекс потребительских расходов.
На основе анализа матрицы коэффициентов парной корреляции делаем вывод о целесообразности построения двухфакторного регрессионного уравнения Y=f(X2, X5).
Построение линейного уравнения регрессии.
По заданию необходимо было построить регрессионную модель со значимыми факторами в линейной форме.
Оценка параметров регрессии осуществляется по методу наименьших квадратов. Для проведения регрессионного анализа с помощью пакета SPSS выполним следующие действия:
1. Выберем в верхней строке меню Анализ – Регрессия – Линейная.
2. Поместим переменную Y в поле для зависимых переменных, объявив переменные X1, X2, X2, X4, X5 независимыми (Рис. 2.3).
3. Используется установленный по умолчанию в поле «Метод» Исключение.
4. В полях панели Статистики следует отметить флажками Оценки, Согласие модели и критерий Дурбина-Уотсона (в нашей литературе – критерий Дарбина-Уотсона) (Рис. 2.4), затем нажмите Продолжить.
5. В полях панели Сохранить отметьте необходимые поля (Рис. 2.5) и нажмите Продолжить.
6. Не меняйте значения, установленные по умолчанию в полях панели Параметры. Они будут использованы для определения критерия Фишера с доверительной вероятностью 0,95.
|
|
|
7. Начните вычисления нажатием ОК.

Рис. 2.3. Диалоговое окно Линейная регрессия.
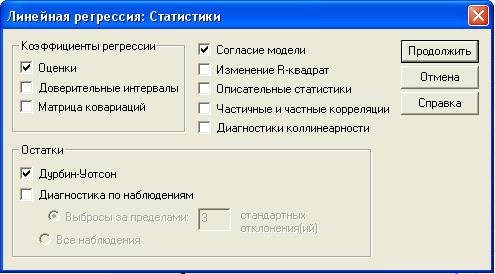
Рис. 2.4. Диалоговое окно Линейная регрессия: Статистики.

Рис.2.5. Диалоговое окно Линейная регрессия: Сохранить.
Результаты регрессионного анализа приведены в следующих таблицах.
При последовательном подборе переменных в SPSS предусмотрена автоматизация, основанная на значимости включения и исключения переменных.
В табл. 2.2 перечислены переменные, которые были последовательно исключены на каждом шаге.
Регрессия
Таблица 2.2. Включенные/исключенные переменные
| Модель | Включенные переменные | Исключенные переменные | Метод |
| Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Цена товара (руб.), Время(a) | . | Принудительное включение | |
| . | Цена товара (руб.) | Исключение (критерий: вероятность F-исключения >=.100). | |
| . | Средняя цена товара у конкурентов (руб.) | Исключение (критерий: вероятность F-исключения >=.100). | |
| . | Время | Исключение (критерий: вероятность F-исключения >=.100). |
a Включены все запрошенные переменные
b Зависимая переменная: Объём реализации (млн. руб.)
В табл. 2.3 приведены значения коэффициента детерминации, коэффициента множественной корреляции, стандартная ошибка, коэффициент Дарбина – Уотсона последовательно для всех моделей. В последней строке приводятся данные для окончательной модели.
Таблица 2.3. Сводка для модели
| Модель | R | R квадрат | Скорректированный R квадрат | Стд. ошибка оценки | Дурбин-Уотсон |
| .944(a) | .891 | .836 | 41.649 | ||
| .943(b) | .889 | .848 | 40.044 | ||
| .939(c) | .882 | .852 | 39.537 | ||
| .927(d) | .859 | .837 | 41.473 | 1.357 |
a Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Цена товара (руб.), Время
b Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Время
c Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.), Время
d Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.)
|
|
|
e Зависимая переменная: Объём реализации (млн. руб.)
В табл. 2.4 приведены результаты дисперсионного анализа и значения F-критерия, полученные на каждом шаге.
Таблица 2.4. Дисперсионный анализ(e)
| Модель | Сумма квадратов | ст.св. | Средний квадрат | F | Знч. | |
| Регрессия | 141371.778 | 28274.356 | 16.300 | .000(a) | ||
| Остаток | 17346.660 | 1734.666 | ||||
| Итого | 158718.437 | |||||
| Регрессия | 141079.525 | 35269.881 | 21.995 | .000(b) | ||
| Остаток | 17638.912 | 1603.537 | ||||
| Итого | 158718.437 | |||||
| Регрессия | 139960.250 | 46653.417 | 29.845 | .000(c) | ||
| Остаток | 18758.188 | 1563.182 | ||||
| Итого | 158718.437 | |||||
| Регрессия | 136358.334 | 68179.167 | 39.639 | .000(d) | ||
| Остаток | 22360.104 | 1720.008 | ||||
| Итого | 158718.437 |
a Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Цена товара (руб.), Время
b Предикторы: (константа) Индекс потребительских расходов (%), Средняя цена товара у конкурентов (руб.), Расходы на рекламу (тыс. руб.), Время
c Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.), Время
d Предикторы: (константа) Индекс потребительских расходов (%), Расходы на рекламу (тыс. руб.)
e Зависимая переменная: Объём реализации (млн. руб.)
В табл. 2.5 в первом столбце указан номер модели, во втором – перечисляются используемые в модели независимые переменные, а в третьем столбце содержаться коэффициенты уравнения регрессии. В четвертом столбце содержаться стандартные ошибки коэффициентов уравнения регрессии, в пятом – стандартизованные коэффициенты, а в шестом – t- статистика, используемая для проверки значимости коэффициентов уравнения регрессии.
Таблица 2.5. Коэффициенты(a)
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | t | Знч. | ||
| B | Стд. ошибка | Бета | ||||
| (Константа) | -3017.396 | 1094.485 | -2.757 | .020 | ||
| Время | -13.419 | 10.378 | -.621 | -1.293 | .225 | |
| Расходы на рекламу (тыс. руб.) | 6.672 | 3.009 | .319 | 2.218 | .051 | |
| Цена товара (руб.) | -6.477 | 15.779 | -.067 | -.410 | .690 | |
| Средняя цена товара у конкурентов (руб.) | 12.238 | 14.410 | .136 | .849 | .416 | |
| Индекс потребительских расходов (%) | 30.476 | 11.525 | 1.337 | 2.644 | .025 | |
| (Константа) | -2914.326 | 1024.234 | -2.845 | .016 | ||
| Время | -12.569 | 9.778 | -.582 | -1.285 | .225 | |
| Расходы на рекламу (тыс. руб.) | 7.125 | 2.691 | .340 | 2.648 | .023 | |
| Средняя цена товара у конкурентов (руб.) | 7.930 | 9.492 | .088 | .835 | .421 | |
| Индекс потребительских расходов (%) | 29.151 | 10.637 | 1.279 | 2.740 | .019 | |
| (Константа) | -2957.613 | 1009.969 | -2.928 | .013 | ||
| Время | -14.316 | 9.431 | -.663 | -1.518 | .155 | |
| Расходы на рекламу (тыс. руб.) | 7.229 | 2.654 | .345 | 2.724 | .018 | |
| Индекс потребительских расходов (%) | 30.951 | 10.285 | 1.358 | 3.009 | .011 | |
| (Константа) | -1471.314 | 259.766 | -5.664 | .000 | ||
| Расходы на рекламу (тыс. руб.) | 9.568 | 2.266 | .457 | 4.223 | .001 | |
| Индекс потребительских расходов (%) | 15.753 | 2.467 | .691 | 6.386 | .000 |
a Зависимая переменная: Объём реализации (млн. руб.)
|
|
|
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов, полученное на последнем шаге можно записать в следующем виде:
y = -1471.314 + 9.568х1 + 15.754х2
Коэффициенты уравнения регрессии показывают, что при увеличении Затрат на рекламу на одну тыс. руб. Объём реализации увеличится на 9,568 млн. руб., при увеличении Индекса потребительских расходов на один % Объём реализации увеличится на 15,754 млн. руб.
ОЦЕНКА КАЧЕСТВА МОДЕЛИ
Оценка качества всего уравнения регрессии.
Оценка качества уравнения регрессии производится с помощью коэффициентов детерминации R  и множественной корреляции R. Их значения можно найти в табл. 2.3 Сводка для модели.
и множественной корреляции R. Их значения можно найти в табл. 2.3 Сводка для модели.
Коэффициент детерминации R  = 0,859 показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
= 0,859 показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
Коэффициент множественной корреляции R = 0,927 показывает тесноту связи зависимой переменной Y со всеми включенными в модель объясняющими факторами.
Проверка значимости уравнения регрессии по F-критерию Фишера.
Проверку значимости уравнения регрессии произведем на основе F-критерия Фишера. Значение критерия Фишера F = 39.639 можно найти в табл. 2.4 Дисперсионный анализ.
Вероятность ошибки  , соответствующая расчетному значению F-критерия, выводится в правой колонке под заголовком "Значимость". Ее величина свидетельствует о значимости уравнения регрессии (р < 0,001).
, соответствующая расчетному значению F-критерия, выводится в правой колонке под заголовком "Значимость". Ее величина свидетельствует о значимости уравнения регрессии (р < 0,001).
|
|
|


