 |
Тема 2. Элементы линейной алгебры
|
|
|
|
Системы линейных уравнений
Дана система трёх линейных уравнений с тремя неизвестными.  (2.1)
(2.1)
Матричный метод решения систем линейных уравнений
Систему уравнений (2.1) можно представить в матричном виде  , где
, где  − основная матрица системы,состоящая из коэффициентов уравнений при неизвестных;
− основная матрица системы,состоящая из коэффициентов уравнений при неизвестных; 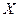 − матрица-столбец неизвестных
− матрица-столбец неизвестных  ;
;  − матрица-столбец свободных членов системы.
− матрица-столбец свободных членов системы.
Исходную систему уравнений (2.1) можно представить в матричном виде  , где
, где  − основная матрица системы,состоящая из коэффициентов уравнений при неизвестных, причём матрица
− основная матрица системы,состоящая из коэффициентов уравнений при неизвестных, причём матрица  квадратная(содержит одинаковое число строк и столбцов);
квадратная(содержит одинаковое число строк и столбцов); 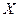 − матрица-столбец неизвестных
− матрица-столбец неизвестных  ;
;  − матрица-столбец свободных членов системы:
− матрица-столбец свободных членов системы:  .
.
Если матрица 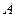 невырожденная, т.е. определитель матрицы отличен от нуля
невырожденная, т.е. определитель матрицы отличен от нуля  , то исходная система уравнений имеет единственное решение, которое находится по формуле
, то исходная система уравнений имеет единственное решение, которое находится по формуле  , (2.2) где
, (2.2) где  − обратная матрица к матрице
− обратная матрица к матрице  .
.
Определитель третьего порядка матрицы  вычисляется по формуле
вычисляется по формуле

Обратная матрицанаходится по формуле 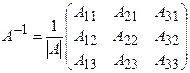 . (2.3)
. (2.3)
Алгебраические дополнения  элементов
элементов  матрицы
матрицы 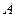 находятся по формуле
находятся по формуле  , где
, где  – минор элемента
– минор элемента  матрицы
матрицы 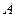 , представляющий собой определитель, полученный из основного
, представляющий собой определитель, полученный из основного  вычёркиванием
вычёркиванием  - й строки и
- й строки и  - го столбца.
- го столбца.
Пример 5
Решить систему уравнений матричным методом 
Решение: 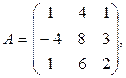
 Матричный вид данной системы уравнений:
Матричный вид данной системы уравнений: 
Вычислим определитель матрицы А.  Т.к. определитель матрицы А не равен 0, то матрица А невырожденная, для неё существует обратная матрица A-1.
Т.к. определитель матрицы А не равен 0, то матрица А невырожденная, для неё существует обратная матрица A-1.
Вычислим алгебраические дополнения  для каждого элемента
для каждого элемента  основной матрицы.
основной матрицы.









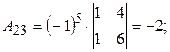



Таким образом, имеем следующую обратную матрицу:

Тогда матричное решение исходной системы 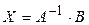 имеет вид:
имеет вид:
|
|
|
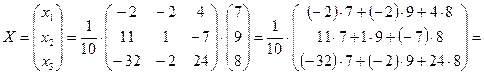

Проверка:
Подставим найденные числа вместо переменных  в исходную систему уравнений
в исходную систему уравнений 
Получили верные числовые равенства, следовательно, решение найдено верно.
Ответ: 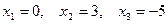 .
.
Метод Крамера
Рассмотрим решение системы (2.1) с помощью формул Крамера 
Дополнительные определители  получаются из основного Δ, если в нём заменить соответственно первый, второй, … n-й столбец на столбец свободных членов системы.
получаются из основного Δ, если в нём заменить соответственно первый, второй, … n-й столбец на столбец свободных членов системы.
Таким образом, для решения системы (2.1) с учетом уже введённых обозначений, дополнительные определители будут иметь вид:

Пример 6 Решить систему уранений, рассмотренную в примере 5, по правилу Крамера.


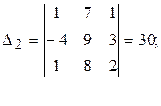
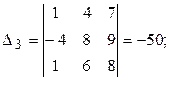

Тема 3. Теория пределов
Предел функции
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
Определение. Число  называется пределом функции
называется пределом функции  в точке
в точке  (или при
(или при  ), если для любого, сколь угодно малого положительного числа
), если для любого, сколь угодно малого положительного числа  найдётся такое положительное число
найдётся такое положительное число 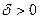 , зависящее от
, зависящее от  , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  ,
,  выполняется неравенство
выполняется неравенство  .
.
Этот предел функции обозначается: 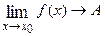 или ƒ(х)→А при х→х0.
или ƒ(х)→А при х→х0.
Практическое вычисление пределов основывается на следующих теоремах: если существуют  и
и 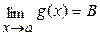 , то
, то
1)  ; (3.1)
; (3.1)
2)  ; (3.2)
; (3.2)
3) 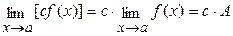 ; (3.3)
; (3.3)
4)  (при
(при  ). (3.4)
). (3.4)
Определение. Функция α (х) называется бесконечно малой величиной при х→х0, или при х→∞, если её предел равен нулю 
Определение. Функция ƒ(х) называется бесконечно большой в точке х0 (или при х→х0), если имеет место одно из равенств: 
 .
.
Теорема (о связи бесконечно большой и бесконечно малой функций): если ƒ(х) ─ бесконечно малая функция при х→х0, то 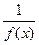 ─ бесконечно большая функция при х→х0, и наоборот.
─ бесконечно большая функция при х→х0, и наоборот.
Первый замечательный предел  . (3.5)
. (3.5)
Второй замечательный предел  . (3.6)
. (3.6)
Пример 7 Найти предел 
Решение: Поскольку функция непрерывна в точке 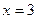 , искомый предел равен значению функции в этой точке. Используя теоремы о действиях над пределами функций, получим
, искомый предел равен значению функции в этой точке. Используя теоремы о действиях над пределами функций, получим
|
|
|

Пример 8 Найти предел 
Решение: При 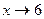 числитель
числитель  стремится к пяти
стремится к пяти  (т.е. является ограниченной функцией), а знаменатель
(т.е. является ограниченной функцией), а знаменатель  – к нулю (т.е. является бесконечно малой величиной). Очевидно, что их отношение есть величина бесконечно большая, т. е.
– к нулю (т.е. является бесконечно малой величиной). Очевидно, что их отношение есть величина бесконечно большая, т. е.

В рассмотренных примерах предел находился сразу, чаще при вычислении пределов мы сталкиваемся с неопределённостями:  ,
,  ,
, 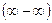 ,
,  .
.
Пример 9 Найти предел 
Решение: При  числитель и знаменатель дроби равны нулю, имеем неопределенность вида
числитель и знаменатель дроби равны нулю, имеем неопределенность вида  . Чтобы раскрыть неопределённость вида
. Чтобы раскрыть неопределённость вида  , необходимо разложить числитель и знаменатель на множители и сократить их на общий множитель
, необходимо разложить числитель и знаменатель на множители и сократить их на общий множитель  .
.

Пример 10 Найти предел 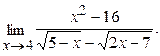
Решение: Непосредственная подстановка предельного значения аргумента 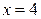 приводит к неопределённости вида
приводит к неопределённости вида  . Избавимся от иррациональности в знаменателе, умножив числитель и знаменатель дроби на выражение
. Избавимся от иррациональности в знаменателе, умножив числитель и знаменатель дроби на выражение  .
. 


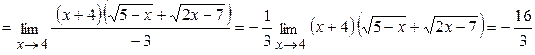 .
.
Пример 11  .
.
Решение: Теорему о пределе частного здесь применить нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В данном случае имеет место неопределённость вида  . Разделим числитель и знаменатель дроби на х в высшей степени (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
. Разделим числитель и знаменатель дроби на х в высшей степени (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:

Пример 12
Найти предел 
Решение: Приведём дроби к общему знаменателю:

Числитель и знаменатель дроби – бесконечно большие функции, поэтому здесь имеет место неопределённость вида  . Раскрывая эту неопределённость, разделим числитель и знаменатель дроби на высшую степень
. Раскрывая эту неопределённость, разделим числитель и знаменатель дроби на высшую степень  , т. е. на
, т. е. на 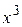 :
:
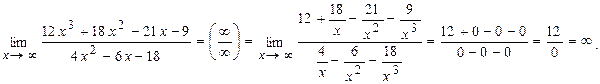
Пример 13 Найти предел 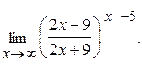
Решение: При 
 , а показатель степени
, а показатель степени  стремится к
стремится к  , следовательно, имеем неопределённость вида
, следовательно, имеем неопределённость вида  .
.
Представим дробь в виде суммы 1 и некоторой бесконечно малой величины: 
 .
. 
Применим второй замечательный предел (3.6).


|
|
|


