 |
Тема 6. Функция двух переменных
|
|
|
|
Определение. Есликаждой паре чисел  по некоторому закону
по некоторому закону  поставлено одно определённое число
поставлено одно определённое число  , то говорят, что на множестве D задана функция Z=f(x,y).
, то говорят, что на множестве D задана функция Z=f(x,y).
Для определения полного дифференциала функции Z=f(x,y) необходимо ввести понятие частной производной нескольких переменных.
Определение. Величина  называется полным приращением функции в точке (х, у). Если задать только приращение аргумента
называется полным приращением функции в точке (х, у). Если задать только приращение аргумента  или только приращения аргумента
или только приращения аргумента  , то полученные приращения функции соответственно:
, то полученные приращения функции соответственно:  и
и  называются частными.
называются частными.
Определение. Частной производной от функции  по независимой переменной
по независимой переменной  называется конечный предел
называется конечный предел  , вычисленный при постоянном
, вычисленный при постоянном  .
.
Определение. Частной производной от функции  по
по  называется конечный предел
называется конечный предел  , вычисленный при постоянном
, вычисленный при постоянном  .
.
Обозначается частная производная так:  или
или 
 .
.
Пример 16 Найти частные производные функций:
a)  ; b)
; b)  .
.
Решение:
а) при нахождении частной производной по х будем рассматривать  как величину постоянную. Получим:
как величину постоянную. Получим:  .
.
Аналогично, дифференцируя по у, считаем  постоянной величиной, т.е.
постоянной величиной, т.е.  ;
;
b) при фиксированном  имеем степенную функцию от х, таким образом,
имеем степенную функцию от х, таким образом,  ;
;
при фиксированном  функция является показательной относительно
функция является показательной относительно  , тогда
, тогда  .
.
Полный дифференциал функции  вычисляется по формуле
вычисляется по формуле
 .
.
Пример 17 Найти полный дифференциал функции  .
.
Решение:  ;
;  ;
;  .
.
Тема 6. Интегральные исчисления
Неопределённый интеграл
Определение. Функция F(x) называется первообразной функцией для функции ƒ(х) на промежутке X, если в каждой точке  этого промежутка
этого промежутка
F/ (x) = f(x).
Если функция f(x) имеет первообразную F(x), то она имеет бесконечное множество первообразных, причём все первообразные содержатся в выражении F(x) + С, где С ─ произвольная постоянная.
|
|
|
Определение. Совокупность всех первообразных функции ƒ(х) на промежутке X называется неопределённым интегралом от функции f(x) и обозначается  т.е.
т.е.  .
.
Свойства неопределённого интеграла
1.  ,
, 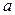 ─постоянное число.
─постоянное число.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
Таблица основных интегралов
| № | Формула | № | Формула |

| 
| ||

| 
| ||
 , , 
| 
| ||

| 
| ||
 , , 
| 
| ||

| 
| ||

| 
|
Пример 18 Найти интеграл  .
.
Решение.

Таблицу интегралов можно расширить, если применить формулы:
а)  , если
, если  ;
;
б)  .
.
Пример 19 Найти интегралы.
а)  ; б)
; б)  ;
;
в)  ;
;
г)  .
.
Замена переменной в неопределённом интеграле
(метод подстановки)
Одним из основных методов интегрирования является метод замены
переменной, описываемый следующей формулой:
 ,
,
где  ─ функция, дифференцируемая на рассматриваемом промежутке.
─ функция, дифференцируемая на рассматриваемом промежутке.
Пример 20 Найти интегралы:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Решение: а)  ;
;
б)  ;
;
в)  ;
;
г) 
Интегрирование по частям
Интегрированием по частям называется нахождение интеграла по формуле
 ,
,
где  ─ непрерывно дифференцируемые функции.
─ непрерывно дифференцируемые функции.
При использовании этой формулы за U берется та функция, которая при дифференцировании упрощается, а за dV - та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Пример 21 Найти интегралы:
a) 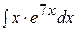 ; б)
; б)  ; в)
; в)  .
.
Решение:
a) 
б) 
в) 
Определенный интеграл
Формула Ньютона – Лейбница
Если функция f(x) непрерывна на отрезке [а;b] и F(x) ─ первообразная для f(x) на этом отрезке, то справедлива формула Ньютона ─ Лейбница
 .
.
Пример 22 Вычислить:  .
.
Решение:

Формула интегрирования по частям

Пример 23

Площадь плоской фигуры
Площадь фигуры, ограниченной сверху непрерывной кривой  , снизу ─ непрерывной кривой
, снизу ─ непрерывной кривой 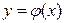 , слева ─ прямой
, слева ─ прямой  , справа прямой
, справа прямой  , вычисляется по формуле
, вычисляется по формуле 
|
|
|
Пример 24 Найти площадь фигуры, ограниченной линиями  .
.
Решение: Определим точки пересечения данных линий. Из уравнения прямой находим 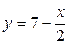 . Решим систему
. Решим систему  .
.

 ,
,  ,
,  .
.
Таким образом, прямая и парабола пересекаются в точках А (-4;9) и В (6;4) (рисунок 6).

Рисунок 6 ─ фигура, ограниченная линиями  .
.
Площадь фигуры равна 
Задания для выполнения контрольной работ
|
|
|


