Мощность электрического тока

Мощность электрического тока показывает работу тока, совершенную в единицу времени
и равна отношению совершенной работы ко времени, в течение которого эта работа была совершена

.

 

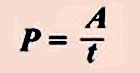
(мощность в механике принято обозначать буквой N, в электротехнике — буквой Р)
так как А = IUt, то мощность электрического тока равна:

 

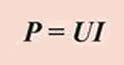
Единица мощности электрического тока в системе СИ:

[ P ] = 1 Вт (ватт) = 1 А. B

 

17.

Электромагнитные колебания — это колебания электрических и магнитных полей, которые сопровождаются периодическим изменением заряда, тока и напряжения. Простейшей системой, где могут возникнуть и существовать электромагнитные колебания, является колебательный контур.

Колебательный контур — это система, состоящая из катушки индуктивности и конденсатора. Если конденсатор зарядить и замкнуть на катушку, то по катушке потечет ток. Когда конденсатор разрядится, ток в цепи не прекратится из-за самоиндукции в катушке. Индукционный ток, в соответствии с правилом Ленца, будет течь в ту же сторону и перезарядит конденсатор. Ток в данном направлении прекратится, и процесс повторится в обратном направлении. Таким образом, в колебательном контуре будут происходить электромагнитные колебания из-за превращения энергии электрического поля конденсатора в энергию магнитного поля катушки с током, и наоборот

Таким образом, в колебательном контуре будут происходить электромагнитные колебания из-за превращения энергии электрического поля конденсатора в энергию магнитного поля катушки с током , и наоборот.

 

Закон Ома в интегральной форме

Закон Ома для участка электрической цепи имеет вид:
U = RI

где:
U — напряжение или разность потенциалов,
I — сила тока,
R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
I=E/(R+r),

где:
e — ЭДС цепи,
I — сила тока в цепи,
R — сопротивление всех элементов цепи,
r — внутреннее сопротивление источника питания.

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
j=σ*E

где
j- вектор плотности тока,
σ — удельная проводимость,
E — вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

19.

http://www.terver.ru/energia_magnitnogo_polja.php

 

 

http://www.physics.ru/courses/op25part2/content/chapter1/section/paragraph10/theory.html

 

http://www.mini-soft.ru/nstu/lab/lab_3_3.php

 

 

22.

ВИДЕМАНА — ФРАНЦА ЗАКОН

утверждает, что отношение коэфф. теплопроводности c к уд. электропроводности s для металлов при одинаковой темп-ре постоянно: c/s=const. Установлен в 1853 экспериментально нем. физиками Г. Видеманом и Р. Францем (R. Franz). В 1881 дат. физик Л. Лоренц экспериментально показал, что это отношение пропорц. Т: c/s=LT, где L — число Лоренца, одинаковое практически для всех металлов при комнатной и более высоких темп-pax Т. В.— Ф. з. впервые был объяснён нем. физиком П. Друде (1902), к-рый рассматривал эл-ны в металле как газ и применил к нему методы кинетич. теории газов (электро- итеплопроводность

металлов обусловливается в осн. движением свободных эл-нов). В дальнейшем на базе квант. статистики для L было получено выражение:

L =(p3/3)(k/e)2=2,45•10-8 ВтОм/К2,

где е — заряд эл-на. При комнатной темп-ре наблюдаемые значения L хорошо согласуются (за нек-рым исключением, напр. для Be) с теоретическими. Отклонение эксперим. значений L от теоретических совр. теория объясняет неупругостью столкновений эл-нов проводимости с колебаниями кристаллической решётки.

 

Зако́н Видема́на — Фра́нца — это физический закон, утверждающий, что для металлов отношение коэффициента теплопроводности К к удельной электрической проводимости пропорционально температуре:

.

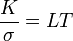
В 1853 г немецкими учёными Г. Видеманом (1826—1899) и Р. Францем (1827—1902) на основании экспериментальных данных было установлено, что для различных металлов при одинаковой температуре отношение практически не изменяется. Пропорциональность этого отношения термодинамической температуре была установлена Лоренцом в 1882 г.

Взаимная связь электрической проводимости и теплопроводности объясняется тем, что оба эти свойства металлов в основном обусловлены движением свободных электронов.

Коэффициент теплопроводности увеличивается пропорционально средней скорости частиц, так как ускоряется перенос энергии. Электропроводность, наоборот, падает, потому что соударения при большой скорости частиц значительно затрудняют перенос энергии.

Друде, применив классическую кинетическую теорию газов, получил значение коэффициента :

,

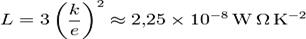
где — постоянная Больцмана, — заряд электрона.

Но только с помощью квантовой статистики Зоммерфельдом было получено значение коэффициента , хорошо согласующееся с экспериментом:

 

 

Явление самоиндукции. Индуктивность. Электромагнитное поле. Явление самоиндукции заключается в появлении ЭДС индукции в самом проводнике при изменении тока в нем. Примером явления самоиндукции является опыт с двумя лампочками, подключенными параллельно через ключ к источнику тока, одна из которых подключается через катушку (рис. 39). При замыкании ключа лампочка 2, включенная через катушку, загорается позже лампочки 1. Это происходит потому, что после замыкания ключа ток достигает максимального значения не сразу, магнитное поле нарастающего тока породит в катушке индукционную ЭДС, которая в соответствии с правилом Ленца будет мешать нарастанию тока. Для самоиндукции выполняется установленный опытным путем закон: ЭДС самоиндукции прямо пропорциональна скорости изменения тока в проводнике. . Коэффициент пропорциональности L называют индуктивностью. Индуктивность — это величина, равная ЭДС самоиндукции при скорости изменения тока в проводнике 1 А/с. Единица индуктивности — генри (Гн). 1 Гн = 1 В • с/А. 1 генри — это индуктивность такого проводника, в котором возникает ЭДС самоиндукции 1 вольт при скорости изменения тока 1 А/с. Индуктивность характеризует магнитные свойства электрической цепи (проводника), зависит от магнитной проницаемости среды сердечника, размеров и формы катушки и числа витков в ней. При отключении катушки индуктивности от источника тока лампа, включенная параллельно катушке, дает кратковременную вспышку Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Энергия магнитного поля находится по формуле Энергия магнитного поля зависит от индуктивности проводника и силы тока в нем. Эта энергия может переходить в энергию электрического поля. Вихревое электрическое поле порождается переменным магнитным полем, а переменное электрическое поле порождает переменное магнитное поле, т. е. переменные электрическое и магнитное поля не могут существовать друг без друга. Их взаимосвязь позволяет сделать вывод о существовании единого электромагнитного поля. Электромагнитное поле — одно из основных физических полей, посредством которого осуществляется взаимодействие электрически заряженных частиц или частиц, обладающих магнитным моментом. Электромагнитное поле характеризуется напряженностью электрического поля и магнитной индукцией. Связь между этими величинами и распределением в пространстве электрических зарядов и токов была установлена в 60-х годах прошлого столетия Дж. Максвеллом. Эта связь носит название основных уравнений электродинамики, которые описывают электромагнитные явления в различных средах и в вакууме. Получены эти уравнения как обобщение установленных на опыте законов электрических и магнитных явлений.

 

 

.

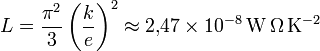
24.

 

Взаимодействие магнитов

С древних времен магнитами называли стержни из специальной руды – магнитного железняка, обладающие определенными свойствами. В настоящее время такими свойствами естественных магнитов обладают искусственные магниты: стальные стержни, обработанные специальным образом. Однако магниты бывают и других форм: кольцевые, подковообразные, шаровые, плоские и др.

Среди особенностей взаимодействия магнитов с окружающими телами выделим те особенности стержневых магнитов, которые показывают, чем отличается магнитное взаимодействие от гравитационного и электростатического:

1. Магнит притягивает железосодержащие предметы: стальные гвозди, скрепки, чугунные трубы, железные опилки. Однако нельзя считать, что магнит обязательно должен притягивать изделия из материалов, которые содержат железо, или, наоборот, совсем не притягивает изделия из материалов, не содержащих железо. Некоторые сорта нержавеющей стали не притягиваются к магнитам, однако к ним притягиваются изделия из окислов хрома, кобальта и никеля.

1. Концы намагниченных стержней сильнее притягивают железосодержащие предметы; это полюсы магнита.
2. Взаимодействуя с земным шаром, намагниченный стержень стремится повернуться так, что один из его концов указывает в сторону северного полюса Земли. Этот полюс магнита получил название северного и обозначается на рисунках буквой N. Противоположный конец стержня называется южным магнитным полюсом и обозначается буквой S.

 

1. Одноименные полюсы магнитов отталкиваются, а разноименные – притягиваются. Поэтому стрелка компаса своим северным полюсом указывает на южный магнитный полюс Земли, лежащий неподалеку от ее северного географического полюса.
   Силы отталкивания одноименных полюсов двух магнитов, расположенных на неизменном расстоянии, одинаковы и равны по модулю силам притяжения, которые возникают между разноименными полюсами тех же магнитов.

 

1. Железосодержащие стержни при трении или контакте с магнитом намагничиваются. Например, если иголка полежит рядом с магнитом, то она начинает самостоятельно притягивать другую иголку.
2. Если изготовить несколько одинаковых тонких постоянных магнитов и собрать их в пучок, как показано на рисунке 4, то сила действия собранного магнита на магнитный полюс другого магнита оказывается пропорциональной числу магнитов в пучке. Последнее свойство позволяет применить принцип суперпозиции для описания взаимодействия магнитов.

 

Попытки обнаружить монополюсный магнит, например разрезая стержневой магнит пополам, оказались безуспешными; у магнита всегда два полюса.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: