Дифракция Фраунгофера на одной щели

Рассмотрим схему наблюдения дифракции Фраунгофера, представленную на рис.3. Плоская монохроматическая волна падает нормально на плоскость Щ, где расположена бесконечно длинная щель шириной b (щель можно считать бесконечно длинной, если ее длина намного больше ее ширины. Так при ширине в 0,01 - 0,05 мм длина в несколько миллиметров может считаться бесконечной).

За щелью расположена линза Л, в фокальной плоскости которой находится экран Э. Наличие линзы равносильно тому, что экран расположен как бы на "бесконечном" расстоянии от объекта. Если бы свет распространялся прямолинейно в соответствии с законами геометрической оптики, то в фокальной плоскости линзы получилась бы бесконечно узкая светлая полоса, проходящая через точку N₀ на экране Э. Но в соответствии с принципом Гюйгенса-Френеля каждая точка волнового фронта, достигающего плоскости, где расположена щель, является источником вторичных волн. Тогда лучи, идущие от всех этих вторичных источников под некоторым углом j к первоначальному направлению, образуют плоский волновой фронт и соберутся в фокальной плоскости линзы в т.N_j (рис.3).

 

Расчет поля в плоскости экрана проведём непосредственно на основе принципа Гюйгенса-Френеля, не используя формулу (1). Для этого разобъем открытую часть поверхности щели на зоны в виде узких полосок одинаковой ширины dх, параллельных краям щели. Эти элементарные участки становятся источниками вторичных волн. Амплитуды dA₀ этих волн, приходящих в т. N_j на экране от разных полосок, одинаковы, так как все зоны имеют одинаковую площадь и одинаковый к направлению вторичных волн угол j. Эти амплитуды будут пропорциональны произведению амплитуды падающей волны Е₀ на размер полоски dx, т.е.

dA₀ = CE₀ dx (2)

где С - коэффициент пропорциональности.

 

Однако фазы колебаний, приходящих от различных участков щели, будут различаться. Для определения разности фаз проведем прямую М₀М_b', перпендикулярную к направлению дифрагированных лучей, и найдем разность хода, возникающую на пути от прямой М₀М_b до прямой М₀М_b'. Из рис.3 видно, что разность хода между волнами, идущими от точки М₀ и от точки М_х, расположенной на расстоянии х от т.М₀, равна хSinj.

Следовательно, если считать, что фаза волны, приходящей в т. N_j из т.М₀, равна нулю, то колебание dU_j, приходящее от элемента dх из окрестности точки М_х в т. N_j, может быть записано в виде:

dU_j = dА₀ cos(wt-kxSinj)

где k=2 p/l - волновое число, w - частота колебания.

Для вычисления величины U_j в т. N_j необходимо просуммировать вклады от различных участков щели, т.е. проинтегрировать dU_j в пределах от х = 0 до х = b:

(3)

Сомножитель cos( w t-1/2kbsin j ) в формуле (3) описывает временное изменение поля в точке наблюдения с частотой w, а модуль выражения, стоящего перед косинусом, есть амплитуда A_j результирующей волны в точке N_j Эти направления примерно соответствуют значениям u, равным u_1max= 1.43p@3p/2, u_2max= 2.46p@5p/2, u_3max= 3.47p@ 7p/2,... Соотношения интенсивностей главного и последующего максимумов равны I_0max = I_1max = I_2max = I_3max =... = 1: 0,045: 0, 016: 0,008:. и не зависят ни от ширины щели, ни от длины волны.

В то же время для направлений Sinj = l/b, 2l/b, 3l/b, 4l/b..., удовлетворяющих уравнению Sin u = 0, интенсивность равна нулю. Эти направления соответствуют случаю, когда разность хода между волнами, приходящими от крайних участков щели, равна целому числу длин волн. Это означает, что для любого произвольно выбранного участка щели всегда найдется другой, равный по величине, участок, излучение от которого придет строго в противофазе с излучением от выбранного участка. Тем самым, в результате интерференции интенсивность распространяющегося в этих направлениях излучения будет равна нулю.

Из рис.4 видно, что основная часть светового потока сосредоточена в центральной дифракционной полосе, определяемой значениями Sinj =l/b (так называемый центральный максимум), малая его часть будет распространяться в пределах первых (около 5%) и вторых (около 2%) максимумов и т.д.

Рис.5. Дифракция Фраунгофера на одной щели: 1 - узкая щель, 2 - широкая щель.

Рассмотрим влияние ширины щели на распределение интенсивности дифракционной картины (рис.5). Увеличение ширины щели приводит к приближению первых минимумов к центру дифракционной картины, при этом резкость дифракционного максимума увеличивается (рис.5, кривая 2). Соотношение интенсивностей света в отдельных максимумах не изменяется, однако увеличивается абсолютное значение интенсивности, связанное с тем, что с увеличением ширины щели увеличивается энергия проходящего через нее излучения.

В заключении отметим, что дифракция Фраунгофера может наблюдаться и при падении сферической волны на объект, и при отсутствии линзы. Из формулы (1) можно показать, что условия для наблюдения дифракции Фраунгофера имеют вид: b²/lr <<1, b²/ls <<1.

32.

Зоны Френеля, участки, на которые можно разбить поверхность световой (или звуковой) волны для вычисления результатов дифракции света (или звука). Впервые этот метод применил О. Френель в 1815—19. Суть метода такова. Пусть от светящейся точки Q (рис.) распространяется сферическая волна и требуется определить характеристики волнового процесса, вызванного ею в точке Р. Разделим поверхность волны S на кольцевые зоны; для этого проведём из точки Р сферы радиусами PO, Pa = PO + l/2; Pb = Pa + l/2, Pc = Pb + l/2, (О — точка пересечения поверхности волны с линией PQ; l — длина световой волны). Кольцеобразные участки поверхности волны, «вырезаемые» из неё этими сферами, и называется Зоны Френеля Волновой процесс в точке Р можно рассматривать как результат сложения колебаний, вызываемых в этой точке каждой Зоны Френеля в отдельности. Амплитуда таких колебаний медленно убывает с возрастанием номера зоны (отсчитываемого от точки О), а фазы колебаний, вызываемых в Р смежными зонами, противоположны. Поэтому волны, приходящие в Р от двух смежных зон, гасят друг друга, а действие зон, следующих через одну, складывается. Если волна распространяется, не встречая препятствий, то, как показывает расчёт, её действие (сумма воздействий всех Зоны Френеля) эквивалентно действию половины первой зоны. Если же при помощи экрана с прозрачными концентрическими участками выделить части волны, соответствующие, например, N нечётным зонам Френеля, то действие всех выделенных зон сложится и амплитуда колебаний Uнечёт в точке Р возрастёт в 2N раз, а интенсивность света в 4N2 раз, причём освещённость в точках, окружающих Р, уменьшится. То же получится при выделении только чётных зон, но фаза суммарной волны Uчёт будет иметь противоположный знак.
Метод Зоны Френеля позволяет быстро и наглядно составлять качественное, а иногда и довольно точное количественное представление о результате дифракции волн при различных сложных условиях их распространения. Он применяется поэтому не только в оптике, но и при изучении распространения радио- и звуковых волн для определения эффективной трассы «луча», идущего от передатчика к приёмнику; для выяснения того, будут ли при данных условиях играть роль дифракционные явления; для ориентировки в вопросах о направленности излучения, фокусировке волн и т.п.

 

Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).

Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии от точки M.

Точки сферы S, находящиеся на расстояниях , , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M .

33.

Интерференция в тонких пленках

 

Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта. Один из способов, использующих такой метод, – опыт Поля. В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки (рис. 8.7). В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.

Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S ₁ и S ₂ источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.

Полосы равного наклона

Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 8.8).

В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точке P такая же, как на линии DC:

 

 

35.

 

Кольца Ньютона

На рис. 8.12 изображена оправа, в которой зажаты две стеклянные пластины. Одна из них слегка выпуклая, так что пластины касаются друг друга в какой-то точке. И в этой точке наблюдается нечто странное: вокруг нее возникают кольца. В центре они почти не окрашены, чуть дальше переливаются всеми цветами радуги, а к краю теряют насыщенность цветов, блекнут и исчезают.

Так выглядит эксперимент, в XVII веке положивший начало современной оптике. Ньютон подробно исследовал это явление, обнаружил закономерности в расположении и окраске колец, а также объяснил их на основе корпускулярной теории света.

Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла (рис. 8.13), называют кольцами Ньютона.

Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны , разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π. Толщина h воздушного зазора связана с расстоянием r до точки касания

 

Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света.

Полосы равной толщины можно наблюдать и с помощью интерферометра Майкельсона, если одно из зеркал з1 или з2 отклонить на небольшой угол.

Итак, полосы равного наклона получаются при освещении пластинки постоянной толщины рассеянным светом, в котором содержатся лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) параллельным пучком света. Полосы равной толщины локализованы вблизи пластинки.

Принцип Гюйгенса–Френеля

 

Дифракция света – в узком, но наиболее употребительном смысле – огибание лучами света границы непрозрачных тел (экранов); проникновение света в область геометрической тени. Наиболее рельефно дифракция света проявляется в областях резкого изменения плотности потока лучей: вблизи каустик, фокуса линзы, границ геометрической тени и др. дифракция волн тесно переплетается с явлениями распространения и рассеяния волн в неоднородных средах. Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями, размеры которых сравнимы с длиной волны, и связанных с отклонениями от законов геометрической оптики. Огибание препятствий звуковыми волнами (дифракция звуковых волн) наблюдается нами постоянно (мы слышим звук за углом дома). Для наблюдения дифракции световых лучей нужны особые условия, это связано с малой длиной световых волн. Между интерференцией и дифракцией нет существенных физических различий. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 9.1). Каждая точка участка волнового фронта, выделенного отверстием, служит источником вторичных волн (в однородной изотопной среде они сферические).

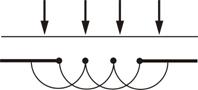
Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. волна огибает края отверстия.

Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде и интенсивности волн, распространяющихся по разным направлениям.

Решающую роль в утверждении волновой природы света сыграл О. Френель в начале XIX века. Он объяснил явление дифракции и дал метод ее количественного расчета. В 1818 году он получил премию Парижской академии за объяснение явления дифракции и метод его количественного расчета.

Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.

При рассмотрении дифракции Френель исходил из нескольких основных положений, принимаемых без доказательства. Совокупность этих утверждений и называется принципом Гюйгенса–Френеля.

Согласно принципу Гюйгенса, каждую точку фронта волны можно рассматривать как источник вторичных волн.

Френель существенно развил этот принцип.

· Все вторичные источники фронта волны, исходящей из одного источника, когерентны между собой.

· Равные по площади участки волновой поверхности излучают равные интенсивности (мощности).

· Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали к волновой поверхности в этой точке. Амплитуда вторичных волн в направлении, составляющем угол α с нормалью, тем меньше, чем больше угол α, и равна нулю при .

· Для вторичных источников справедлив принцип суперпозиции: излучение одних участков волновой поверхности не влияет на излучение других (если часть волновой поверхности прикрыть непрозрачным экраном, вторичные волны будут излучаться открытыми участками так, как если бы экрана не было).

Используя эти положения, Френель уже мог сделать количественные расчеты дифракционной картины.

 

36.

Интерференция света
Явление интерференции свидетельствует о том, что свет — это волна. Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.
Условия интерференции Волны должны быть когерентны. Когерентность -согласованность. В простейшем случае когерентными являются волны одинаковой длины, между которыми существует постоянная разность фаз.
Все источники света, кроме лазера, некогерентны, однако Т. Юнг впервые пронаблюдал (1802) явление интерференции, разделив волну на две с помощью двойной щели. Свет от точечного монохроматического источника S падал на два небольших отвер­стия на экране. Эти отверстия действуют как два когерентных источника светаS1 и S2. Волны от них интерферируют в области перекрытия, проходя разные пути: l1 и l2. На экране наблюдается чередование светлых и темных полос.
Условие максимума. Пусть разность хода между двумя точками , тогда условие максимума: , т. е. на разности хода волн укладывается четное число полуволн (k= 1, 2, 3,...).
Условие минимума Пусть разность хода между двумя точками , тогда условие минимума: , т. е. на разности хода волн укладывается нечетное число полуволн (k= 1, 2, 3,...).
Интерференция света в тонких пленках Различные цвета тонких пленок — результат интерфе­ренции двух волн, отражаю­щихся от нижней и верхней по­верхностей пленки. При отражении от верх­ней поверхности пленки проис­ходит потеря полуволны. Тогда условие максимального усиле­ния интерферирующих лучей в отраженном свете следую­щее: . .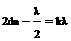
Кольца Ньютона Интерференционная карти­на в тонкой прослойке воздуха между стеклянными пластина­ми — кольца Ньютона. Волна 1 — результат отра­жения ее от точки А (граница стекло —воздух). Волна 2 — отражение от плоской пласти­ны (точка В, граница воздух — стекло). Волны когерентны: возникает интерференционная картина в прослойке воздуха между точками А и В в виде-концентрических колец. Зная радиусы колец, можно вычислить длину волны, используя формулу , где r - радиус кольца, R — радиус кри­визны выпуклой поверхности линзы.
Использование интерференции в технике
Проверка качества обра­ботки поверхности до одной де­сятой длины волны. Несовершенство обра­ботки определяют но искрив­лению интерференционных по­лос, образующихся при отра­жении света от проверяемой поверхности. Интерферометры служат для точного измерения показателя преломления газов и других веществ, длин световых волн.
Просветление оптики. Объективы фотоаппаратов и кинопроекторов, перископы под­водных лодок и другие оптические устройства состоят из большого числа оптических стекол, линз, призм. Каждая отполиро­ванная поверхность стекла отражает около 5% падающего на нее света. Чтобы уменьшить долю отражаемой энергии, исполь­зуется явление интерференции света.
На поверхность оптическо­го стекла наносят тонкую пленку. Для того чтобы волны 1 и 2 ослабляли друг друга, должно выполняться условие минимума. В отраженном свете разность хода волн равна: (происходит потеря полуволны). Следо­вательно, , где n - показатель преломления пленки; h — толщина пленки. Минимальная толщина пленки будет при k=0. Поэтому . При равенстве амплитуд гашение света будет полным. Толщину пленки, следовательно, подбирают так, чтобы пол­ное гашение при нормальном падении имело место для длин волн средней части спектра, тогда для зеленого цвета .   Лучи красного и фиолетового цвета ослабляются незначительно.поэтому объективы оптических приборов в отраженном свете имеют сиреневые оттенки

 

37.

 

Поляризация света. Виды поляризации. Закон Малюса. Поляризация света при отражении и преломлении. Закон Брюстера. Двойное лучепреломление. Искусственная оптическая анизотропия. Вращение плоскости поляризации.

1.
Свет, испускаемый обычными источниками излучения, представляет собой множество квантов, каждом из которых электрический вектор направлен в произвольном направлении, перпендикулярном направлению распространения луча. Такой свет называется естественным или неполяризованным.

1.
Если в пучке света имеется преимущественное направление колебаний электрического вектора, такой свет называется частично поляризованным.

2.
Поляризацией называется выделение линейно поляризованного света из естественного или частично поляризованного света.

3.
Устройства, позволяющие выделять линейно поляризованный свет из естественного или частично поляризованного света, называются поляризаторами. Их действие основано на поляризации света при его отражении или преломлении на границе раздела двух сред.

4.
Эти же устройства можно использовать в качестве анализаторов – устройств, позволяющих определить характер и степень поляризации.

5.
Степенью поляризации называется величина

 

 

2.

2. Если на поляризатор перпендикулярно его плоскости падает линейно поляризованный свет, электрический вектор которого направлен вдоль линии р-р, то падающий свет можно представить в виде двух волн, линейно поляризованных в двух взаимно перпендикулярных плоскостях. Поляризатор пропускает свет, электрический вектор которого направлен вдоль линии а-а, и не пропускает свет, электрический вектор которого направлен в перпендикулярном направлении.

1.
Амплитуда света, выходящего из поляризатора, равна

Соответственно интенсивности линейно поляризованного света I_a и падающего на поляризатор света I_p связаны между собой уравнением

(закон Малюса)

1. Плоскость поляризации света (плоскость колебаний электрического вектора), пропускаемого поляризатором, называется главной плоскостью поляризации.

2.
При изучении закономерностей поляризации естественного света при отражении и преломлении от поверхности раздела двух сред этот свет удобно рассматривать как совокупность двух линейно поляризованных волн – s- и р-типа.

1.
В волне р-типа вектор Е_р лежит в плоскости падения, а в волне s-типа вектор Е_s лежит перпендикулярно плоскости падения.

2.
Коэффициент отражения волн s-типа всегда больше коэффициента отражения волн р-типа, а потому отраженный и преломленный лучи частично поляризованы – в отраженном луче преобладают волна s-типа, а в преломленном луче - р-типа.

3.
Отраженный свет полностью линейно поляризован при угле падения i _Бр (угол Брюстера), удовлетворяющем условию

tg i _Бр = n ₁₂ (закон Брюстера)

 

 

38.

Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.

Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика

 

где N - число молекул в объеме . Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса.

В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов).

Электронный тип поляризации характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле (рис. 2.1) положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля

 

Ориентационнный тип поляризации характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.

 

 

 

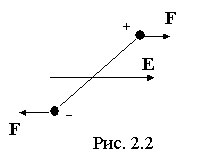
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля.

Такая поляризация называется ориентационной. Поляризованность в этом случае равна , где < p > - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.

Решеточный тип поляризации характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной. Поляризованность и в этом случае можно определить как , где - значение дипольного момента элементарной ячейки, n - число ячеек в единице объема.

 

 

 

39.

Тонкие линзы. Изображение предметов с помощью линз

Раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах, называется геометрической оптикой. Под световыми лучами понимают нормальные к волновым поверхностям линии, вдоль которых распространяется поток световой энергии. Геометрическая оптика, оставаясь приближенным методом построения изображений в оптических системах, позволяет разобрать основные явления, связанные с прохождением через них света, и является поэтому основой теории оптических приборов.

Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая — сферическая или плоская), преломляющими световые лучи, способные формировать оптические изображения предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т. п. По внешней форме (рис. 232) линзы делятся на: 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые. По оптическим свойствам линзы делятся на собирающие и рассеивающие.

Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. Прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью. Для всякой линзы существует точка, называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Оптический центр О линзы для простоты будем считать совпадающим с геометрическим центром средней части линзы (это справедливо только для двояковыпуклой и двояковогнутой линз с одинаковыми радиусами кривизны обеих поверхностей; для плосковыпуклых и плосковогнутых линз оптический центр О лежит на пересечении главной оптической оси со сферической поверхностью).

Линзы с положительной оптической силой являются собирающими, с отрицательной — рассевающими. Плоскости, проходящие через фокусы линзы перпендикулярно ее главной оптической оси, называются фокальными плоскостями. В отличие от собира­ющей рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси

 

Построение изображения предмета в линзах осуществляется с помощью следующих лучей:

1) луча, проходящего через оптический центр линзы и не изменяющего своего направления;

2) луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы;

3) луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно ее главной оптической оси.

Для примера приведены построения изображений в собирающей (рис. 236) и в рас­сеивающей (рис. 237) линзах: действительное (рис. 236, а) и мнимое (рис. 236, б)изображения — в собирающей линзе, мнимое — в рассеивающей.

 

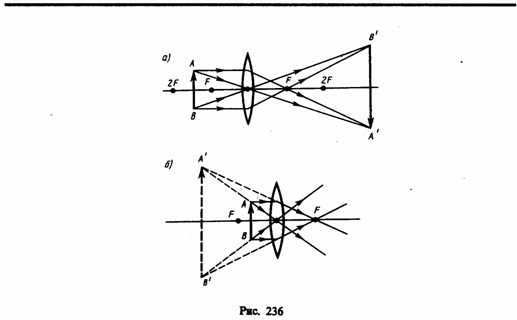
Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевернутое), положительным — мнимое изображение (оно прямое). Комбинации собирающих и рассеивающих линз применяются в оптических приборах, используемых для решения различных научных и технических задач.

 

40.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: