 |
Постановка экономико – математичекой задачи оптимизации рациона кормления скота
|
|
|
|
Рассчитать оптимальный кормовой рацион, учитывающий зоотехнические требования, при помощи традиционных методов подбора очень сложно, а при большом наборе кормов практически невозможно, поэтому задачу целесообразно решать с помощью экономико-математических методов и ЭВМ.
Целевую установку можно выразить следующим образом:
Из имеющихся в наличии кормов составить такой рацион, который по содержанию питательных веществ, соотношению отдельных видов и групп полностью отвечал бы требованиям животных и одновременно был самым дешевым. Критерий оптимальности – минимум стоимости рациона.
Основными переменными являются корма, имеющиеся в наличие, а также корма, кормовые и минеральные добавки, которые хозяйство может приобрести. Единицами измерения этих переменных являются кг.ц в зависимости от периода, на который составляется рацион.
В задаче кроме основных могут быть и вспомогательные переменные. Они чаще всего выражают суммарное количество кормовых единиц или перевариваемого протеина в рационе. С помощью этих переменных записывают условия по структуре рациона (удельный вес отдельных групп кормов).
Основные ограничения необходимы для записи условий по балансу питательных веществ. Технико-экономические коэффициенты в этих ограничениях обозначают содержание соответствующих питательных веществ в единице корма (в 1 кг,1 ц). Константы в правой части ограничений (объемы) показывают количество питательных веществ, которое должно содержаться в рационе.
С помощью дополнительных ограничений записывают условия по соотношению отдельных групп кормов в рационе и отдельных видов кормов внутри групп. Если эти соотношения выражены в весовых единицах, то технико-экономическими коэффициентами по основным переменным соответствующих групп кормов являются единицы или величины, характеризующие удельный вес данного вида или группы корма в рационе (коэффициенты пропорциональности). Константы обозначают минимальное или максимальное зоотехнически допустимое количество данной группы корма в рационе.
|
|
|
С помощью вспомогательных ограничений записывают условия по суммарному количеству кормовых единиц и перевариваемого протеина. Технико-экономические коэффициенты по основным переменным (так же, как и в основных ограничениях) отражают содержание питательных веществ в единице корма или кормовых добавок, а по вспомогательным переменным равны –1. Константами в этих ограничениях являются нули.
Для составления модели оптимального рациона кормления скота необходимо установить следующее:
Вид и половозрастную группу скота, для которого рассчитывается рацион; период; живую массу одной головы; планируемую продуктивность;
Содержание питательных веществ в рационе в зависимости от продуктивности животного, животной массы, физиологического состояния;
Предельные нормы скармливания отдельных кормов данному виду скота или допустимые зоотехнические нормы потребления кормов;
Виды кормов и кормовые добавки, из которых могут быть составлены кормовые рационы (смеси);
Содержание всех видов питательных веществ в единице корма или кормовой добавки;
Цену единицы кормов и кормовых добавок.
Рассматриваем пример оптимизации оптимального рациона кормления скота.
Необходимые данные по видам имеющихся в хозяйстве кормов, содержание питательных веществ и стоимости приведены в Таблице 4.1.
Система переменных определяется в соответствии с условиями задачи.
Количество кормов, которые могут войти в рацион обозначим символами:
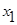 - сено
- сено
|
|
|
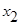 - силос
- силос
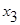 - концентраты
- концентраты
Единица измерения – кг.
Система ограничений. Основными ограничениями в данной модели будут условия по обеспечению всеми питательными веществами (белок, кальций, витамины).
По экономическому содержанию и характеру формализации в модели целесообразно выделить группы ограничений:
I – по балансу питательных веществ;
II – удельному весу кормов суточной выдачи
III – удельному весу кормов в один рацион
IV – влияние на стоимость увеличение ресурсов
I группа ограничений отражает требование к рациону по питательным веществам и показывает, что он должен содержать данное питательное вещество не менее требуемого по норме количества:
ограничение по белку
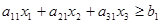
ограничение по кальцию
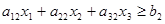
ограничение по витаминам
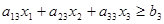
В целях формализации записей приведенных ограничений введем ряд обозначений:
 - индекс ограничения, показывающий порядковый номер элемента питания;
- индекс ограничения, показывающий порядковый номер элемента питания;
 - индекс переменной, показывающий порядковый номер вида
- индекс переменной, показывающий порядковый номер вида
корма в рационе;
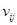 -содержание питательного элемента i-го вида в единице
-содержание питательного элемента i-го вида в единице
(1 кг) j-го вида кома;
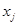 - искомое количество корма j-го вида, входящего в рацион;
- искомое количество корма j-го вида, входящего в рацион;
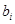 - требуемое по норме количество i-го вида питательного
- требуемое по норме количество i-го вида питательного
вещества в рационе.
С учетом введенных обозначений обобщенная форма записи I группы ограничений будет иметь вид
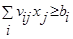 (2.1)
(2.1)
II группа ограничений отражает физиологически допустимые пределы скармливания кормов. Эти дополнительные ограничения показывают верхние пределы отклонений по каждой группе кормов суточной выдачи, представляются следующим образом:
пределы ограничения по физической массе сена
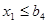
пределы ограничения по физической массе силоса
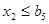
пределы ограничения по физической массе концентратов
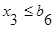
Обобщенная математическая модель записи ограничений II группы имеет вид
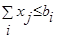 (2.2)
(2.2)
III группа ограничений отражает физиологические, зоотехнические или экономические требования по удельному весу отдельных видов кормов рассчитанных на один рацион.
Ограничения будут записываться так:
органичения по физической массе сена
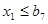
ограничения по физической массе силоса
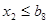
ограничения по физической массе концентратов
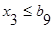
IV группа ограничений будет иметь экспериментальный характер, задача заключается в том, что, как увеличение ресурсов сена и силоса на 1 кг и концентратов на 3 кг. повлияет на оптимальную стоимость.
|
|
|
ограничения по сену
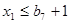
ограничения по силосу
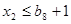
ограничения по концентратам
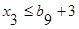
V группа ограничений – неотрицательность переменных величин:
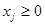
Запишем теперь целевую функцию:
Стоимость рациона должна быть минимальной

Математическая модель целевой функции имеет вид
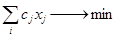 (2.3)
(2.3)
где 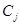 -стоимость (себестоимость) единицы корма j-го вида.
-стоимость (себестоимость) единицы корма j-го вида.
После построения математической модели пришли к выводу, что заданную задачу целесообразно решать модифицированным симплекс – методом.
|
|
|


