Виды средних величин и техника их вычисления

Продукция второго АООТ также составила 12 млрд руб., но план был выполнен на 120%. Ясно, что план второго АООТ равен 10 млрд руб.: 12 х 100/120 = 10 млрд руб.

Отсюда видно, что план обоих АООТ выражался в 16 млрд руб. (6 млрд руб. + 10 млрд руб.), а фактический выпуск продукции — 24 млрд руб. (12 млрд руб. + 12 млрд руб.). Следовательно, сред­ний процент выполнения плана указанных двух АООТ составил не 160%, как получалось при вычислении средней арифметичес­кой, а 150%: 24 х 100/16 = 150%.

Таким образом мы убедились, что средняя арифметическая при­вела к ошибочному результату, она здесь неприменима.

Спрашивается, почему? Потому, что, как уже отмечалось, она может применяться лишь в тех случаях, когда значения при­знаков, из которых вычисляется средняя, увеличиваются или уменьшаются с увеличением или уменьшением характеризуемых ими явлений. В указанном примере мы имеем как раз обратное: процент выполнения плана при одном и том же размере факти­ческой продукции увеличивается с уменьшением установленно­го плана и уменьшается с увеличением этого плана. Другими словами, здесь величина определяющего свойства (сумма пла­нов) обратно пропорциональна величине данного признака (про­цент выполнения плана). Именно в таких случаях и необходимо применять формулу средней гармонической (3), которая равна об-

ратному значению средней арифметической (1), вычисленной из обратных величин (обратная величина равна единице, деленной на прямую величину). В указанном примере, таким образом, сле­дует определить прежде всего среднюю арифметическую из обрат­ных величин. Для удобства вычисления вместо процента возьмем десятичные дроби: 1/2,0+ 1/1,2: 2 = 0,666.

Обратная величина для 0,666, т.е. 1/0,666, равна 1,5, или 150%.

Это и есть средняя гармоническая, точно характеризующая сред­ний процент выполнения плана по обоим АООТ. Она применя­ется также для вычисления, например, покупательной способно­сти денег на основе цен товаров, поскольку цена единицы това­ра при прочих равных условиях обратно пропорциональна поку­пательной способности рубля (чем ниже цена товара, тем боль­ше единиц этого товара можно приобрести на единицу денег). Средняя геометрическая

Этот вид средней вычисляется для установления средних по­казателей темпов роста рядов динамики.

Средняя геометрическая исчисляется путем извлечения корня степени п из произведений отдельных значений признака:

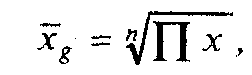
где х — средняя геометрическая, п — число значений признака, а П — знак перемножения.

Предположим, годовые темпы роста продукции какого-либо предприятия составили в 1993 г. — 1,036; в 1994 г. — 1,069; в 1995 г. — 1,084 и в 1996 г. — 1,090. Тогда среднегодовой темп за четырехлетие будет равен:

Обычно на практике вычисление средней геометрической производится с помощью логарифмов по преобразованной фор­муле:

 

 

я-1 В нашем примере средняя геометрическая будет равна

log 4/1,308 = — 0,1168 = 0,02915, 4

Потенцируя, находим VU08 = 1,069, т.е. тот же результат.

 

Глава X. Средние величины и их приме нение в правовой статистике

§ 2, Вида средних ве личин и техника их вычисления

Необходимо иметь в виду, что средняя геометрическая может вычисляться лишь в том случае, когда на протяжении всего пе­риода происходит либо непрерывный рост, либо непрерывное па­дение. При пилообразном характере уровней ряда (т.е. их росте и па­дении — 1,05; 1,1; 1,15; 1,07; 1,3) средний темп роста имел бы фик­тивное значение.

В заключение отметим, что для вычисления рассмотренных вы­ше степенных средних необходимо использовать все имеющиеся зна­чения признака.

В ряде случаев можно определить среднюю величину без про­изводства вычислений, как бы визуально. Для этого используют такие средние величины, как мода и медиана.

Мода и медиана

Мода и медиана определяются лишь структурой распределе­ния. Поэтому их именуют структурными позиционными средними. Медиану и моду используют как среднюю характеристику в тех со­вокупностях, где расчет средней степенной невозможен или не­целесообразен. Для этого в качестве средней берется наиболее ча­сто встречающаяся величина, называемая модой (Мо). Например, 100 уголовных дел по определенному виду преступлений распре­делились за год по срокам расследования таким образом:

Срок расследования, месяцы Число дел

1 30

2 60

3 _Ш

Всего 100

Наибольшее число дел данной категории (наибольший вес — 60) расследуется в течение двух месяцев. Это и будет мода — ва­риант, которому соответствует наибольшая частота в совокупно­сти или в вариационном ряду.

К моде прибегают для выявления величины признака, име­ющей наибольшее распространение (цена на рынке, по которой было совершено наибольшее число продаж данного товара, но­мер обуви, который пользуется наибольшим спросом у покупате­лей, и т.д.). Мода чаще всего используется в совокупностях боль­шой численности.

Медиана (Me) — это средняя вариантов ранжированного (упоря­доченного) ряда, расположенного в определенном порядке — по воз­растанию или убыванию вариантов. Она делит такой ряд пополам.

Например, выборочное обследование в одном из округов Москвы 12 коммерческих пунктов обмена валюты позволило за­фиксировать различные цены за доллар США при его продаже (дан­ные на 17 июля 1997 г. при установленном ЦБ РФ курсе доллара США 5785 руб.).

№ пункта обмена валюты 1 2 3 4 5 6 7 8 9 10 И 12

Цена за 1 долл. США, руб. 5795 5805 5800 5815 5810 5790 5825 5810 5805 5820 5800 5810

Ввиду отсутствия в нашем распоряжении данных об объеме про­даж в каждом обменном пункте расчет средней арифметической с целью определения средней цены за доллар нецелесообразен, да и невозможен. Однако можно определить то значение призна­ка, которое делит единицы ранжированного ряда на две части. Та­кое значение и носит название медианы. Ее расчет по несгруппи-рованным данным производится следующим образом:

а) расположим индивидуальные значения признака в возра­стающем порядке:

XI Х2 ХЗ Х4 XS Х6 Х7 Х8 Х9 Х10 XII XI2 5790 5795 5800 5800 5805 5805 5810 5810 5810 5815 5820 5825

б) определим порядковый номер медианы по формуле

..., я + 1 № Me = —-—.

В нашем случае № Me - 6,5. Это означает, что медиана рас­положена между шестым и седьмым значениями признака в ран­жированном ряду, так как ряд имеет четное число индивидуаль­ных значений. Таким образом, Me равна средней арифметической соседних значений 5805 и 5810:

Me = (5805+5810)/2 = 5807,5 руб.

Иной порядок вычисления медианы в случае нечетного чис­ла индивидуальных значений.

Предположим, мы наблюдали не 12, а 11 пунктов обмена ва­люты, тогда ранжированный ряд будет выглядеть следующим об­разом (отбрасываем 12 пункт):

XI Х2 ХЗ Х4 Х5 Х6 Х7 Х8 Х9 Х10 XII. 5790 5795 5800 5800 5805 5805 5810 5810 5810 5815 5820

 

Глава X, Средние в еличины и их прим енение в правовой статистике

§ 3. Способы расчета показателей вариации

Определяем номер медианы: № Me = (ll + l)/2 = 6; на шестом месте находится Х6 = 5805. Это и есть медиана (Me = 5805 руб.).

Модальной ценой за доллар США можно назвать 5810 руб.: это значение повторяется 3 раза, чаще, чем все другие.

⇐ Предыдущая41424344454647484950Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: