Свободные одномерные колебания

Содержание

Введение

Свободные одномерные колебания

Вынужденные колебания

Колебания систем со многими степенями свободы

Затухающие колебания

Вынужденные колебания при наличии трения

Заключение

Список использованной литературы

Введение

 

Работа посвящена изучению различных колебаний. В механике и акустике, в радиофизике и оптике, в квантовой физике и физике твердого тела — всюду мы сталкиваемся с колебаниями. Единый подход к изучению колебаний основанный на общности уравнений, описывающих колебательные закономерности, позволяет выявить глубокие связи между различными, на первый взгляд, явлениями. Таким образом, изучая колебания, мы будем обращать внимание не только на то, что «волнуется» и что «колеблется», а главным образом на то, как и почему происходят колебания.

Свободные одномерные колебания

 

Очень распространенный тип движения механических систем представляют собой, так называемые малые колебания, которые система совершает вблизи своего положения устойчивого равновесия. Рассмотрение этих движений мы начнем с наиболее простого случая, когда система имеет всего одну степень свободы.

Устойчивому равновесию соответствует такое положение системы, в котором ее потенциальная энергия U(q) имеет минимум; отклонение от такого положения приводит к возникновению силы — dU / dq, стремящейся вернуть систему обратно. Обозначим соответствующее значение обобщенной координаты посредством q0. При малых отклонениях от положения равновесия в разложении разности U(q)—U(q0) по степеням q — q0 достаточно сохранить первый неисчезающий член. В общем случае таковым является член второго порядка

 

 

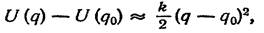
где k — положительный коэффициент (значение второй производной U" (q) при q = q0). Будем в дальнейшем отсчитывать потенциальную энергию от ее минимального значения (т. е. положим U(q0) = 0) и введем обозначение

 

x = q – q ₀                   (1, 1)

 

для отклонения координаты от ее равновесного значения. Таким образом,

 

U (x) = kx ² /2.         (1,2)

Кинетическая энергия системы с одной степенью свободы имеет в общем случае вид

 

 

В том же приближении достаточно заменить функцию a(q) просто ее значением при q = q₀. Вводя для краткости обозначение

 

 

получим окончательно следующее выражение для лагранжевой функции системы, совершающей одномерные малые колебания:

 

   (1,3)

 

Соответствующее этой функции уравнение движения гласит:

  (1,4) или

  (1,5)

 

где введено обозначение

 

               (1,6)

 

Два независимых решения линейного дифференциального уравнения

(1,5): cos ωt и sin ωt, так что его общее решение

 

  (1,7)

Это выражение может быть написано также и в виде

 

    (1,8)

 

Поскольку cos (ωt + α) = cos ωt cos α — sin ωt sin α, то сравнение с (1,7) показывает, что произвольные постоянные  связаны с постоянными

 соотношениями

 

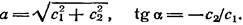 (1.9)

 

Таким образом, вблизи положения устойчивого равновесия система совершает гармоническое колебательное движение. Коэффициент а при периодическом множителе в (1,8) называется амплитудой колебаний, а аргумент косинуса — их фазой; а есть начальное значение фазы, зависящее, очевидно, от выбора начала отсчета времени. Величина ω называется циклической частотой колебаний; в теоретической физике, впрочем, ее называют обычно просто частотой, что мы и будем делать в дальнейшем.

Частота является основной характеристикой колебаний, не зависящей от начальных условий движения. Согласно формуле (1,6) она всецело определяется свойствами механической системы как таковой. Подчеркнем, однако, что это свойство частоты связано с предполагаемой малостью колебаний и исчезает при переходе к более высоким приближениям. С математической точки зрения оно связано с квадратичной зависимостью потенциальной энергии от координаты.

Энергия системы, совершающей малые колебания, есть

 

 

или, подставив сюда (21,8):

                           (1,10)

 

Она пропорциональна квадрату амплитуды колебаний.

Зависимость координаты колеблющейся системы от времени часто оказывается удобным представлять в виде вещественной части комплексного выражения

 

                            (1,11)

 

где А — комплексная постоянная; написав ее в виде

A = ae^ia,                                          (1,12)

 

мы вернемся к выражению (1,8). Постоянную А называют комплексной амплитудой;ее модуль совпадает с обычной амплитудой, а аргумент — с начальной фазой.

Оперирование с экспоненциальными множителями в математическом отношении проще, чем с тригонометрическими, так как дифференцирование не меняет их вида. При этом пока мы производим лишь линейные операции (сложение, умножение на постоянные коэффициенты, дифференцирование, интегрирование), можно вообще опускать знак взятия вещественной части, переходя к последней лишь в окончательном результате вычислений.

Вынужденные колебания

 

Перейдем к рассмотрению колебаний в системе, на которую действует некоторое переменное внешнее поле; такие колебания называют вынужденными в отличие от рассмотренных так называемых свободных колебаний. Поскольку колебания предполагаются по-прежнему малыми, то тем самым подразумевается, что внешнее поле достаточно слабое, в противном случае оно могло бы вызвать слишком большое смещение х.

В этом случае наряду с собственной потенциальной энергией ½ kx ² система обладает еще потенциальной энергией U_{e (} x, t),связанной с действием внешнего поля. Разлагая этот дополнительный член в ряд по степеням малой величины х, получим:

 

 

Первый член является функцией только от времени и потому может быть опущен в лагранжевой функции (как полная производная по t от некоторой другой функции времени). Во втором члене — dUe / dx есть внешняя «сила», действующая на систему в положении равновесия и являющаяся заданной функцией времени; обозначим ее как F (t). Таким образом, в потенциальной энергии появляется член — xF (t), так что функция Лагранжа системы будет:

 

         (2,1)

 

Соответствующее уравнение движения есть

 

 

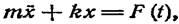
или

 

                              (2,2)

 

где мы снова ввели частоту со свободных колебаний.

Как известно, общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами получается в виде суммы двух выражений: х = х₀ + х 1, где х₀ — общее решение однородного уравнения, a х 1 — частный интеграл неоднородного уравнения. В данном случае х₀ представляет собой рассмотренные свободные колебания.

Рассмотрим представляющий особый интерес случай, когда вынуждающая сила тоже является простой периодической функцией времени с некоторой частотой у:

F (f) = fcos (yt + β).                                 (2,3)

 

Частный интеграл уравнения (2,2) ищем в виде х 1 = b cos (yt +β) стем же периодическим множителем. Подстановка в уравнение дает: b = f / m (ω²- y ²); прибавляя решение однородного уравнения, получим общий интеграл в виде

 

     (2,4)

 

Произвольные постоянные а и α определяются из начальных условий.

Таким образом, под действием периодической вынуждающей силы система совершает движение, представляющее собой совокупность двух колебаний — с собственной частотой системы ω и с частотой вынуждающей силы у.

Решение (2,4) неприменимо в случае так называемого резонанса, когда частота вынуждающей силы совпадает с собственной частотой системы. Для нахождения общего решения уравнения движения в этом случае перепишем выражение,(2,4) с соответствующим переобозначением постоянных в виде

 

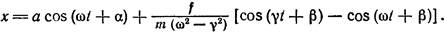
При у → ω и второй член дает неопределенность вида 0/0. Раскрывая ее по правилу Лопиталя, получим:

 

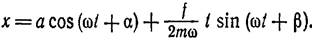                    (2,5)

 

Таким образом, в случае резонанса амплитуда колебаний растет линейно со временем (до тех пор, пока колебания не перестанут быть малыми и вся излагаемая теория перестанет быть применимой).

Выясним еще, как выглядят малые колебания вблизи резонанса, когда

у = ω + ε, где ε — малая величина. Представим общее решение в комплексном виде, как

 

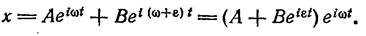              (2,6)

 

Так как величина 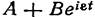  мало меняется в течение периода 2π/ω множителя , то движение вблизи резонанса можно рассматривать как малые колебания, но с переменной амплитудой

Обозначив последнюю через С, имеем:

 

 

Представив А и В соответственно в виде  и  получим:

              (2,7)

 

Таким образом, амплитуда колеблется периодически с частотой ε, меняясь между двумя пределами

 

Это явление носит название биений.

Уравнение движения (2,2) может быть проинтегрировано и в общем виде при произвольной вынуждающей силе F (t), Это легко сделать, переписав его предварительно в виде

 

 или

                              (2,8)

 

где введена комплексная величина

 

                                 (2,9)

 

Уравнение (2,8) уже не второго, а первого порядка. Без правой части его решением было бы

 

 

 

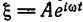
с постоянной А. Следуя общему правилу, ищем решение неоднородного уравнения в виде

 

 

 

и для функции A (t) получаем уравнение

 

Интегрируя его, получим решение уравнения (2,8) в виде

 

             (2, 10)

 

где постоянная интегрирования ε0 представляет собой значение ε в момент времени t = 0. Это и есть искомое общее решение; функция x (t) дается мнимой частью выражения (2,10).

Энергия системы, совершающей вынужденные колебания, разумеется, не сохраняется; система приобретает энергию за счет источника внешней силы. Определим полную энергию, передаваемую системе за все время действия силы (от - ∞ до + ∞), предполагая начальную энергию равной нулю. Согласно формуле (2,10) (с нижним пределом интегрирования - ∞ вместо нуля и с

ξ (-∞) = 0) имеем при t → ∞:

 

 

С другой стороны, энергия системы как таковой дается выражением

 

                           (2,11)

 

Подставив сюда | ξ (∞) |², получим искомую передачу энергии

в виде

 

                          (2,12)

она определяется квадратом модуля компоненты Фурье силы F (t) с частотой, равной собственной частоте системы.

В частности, если внешняя сила действует лишь в течение короткого промежутка времени (малого по сравнению с 1/ω), то можно положить .

Тогда

 

 

Этот результат заранее очевиден: он выражает собой тот факт, что кратковременная сила сообщает системе импульс ∫ F dt, не успев за это время произвести заметного смещения.

123	Поделиться:

Воспользуйтесь поиском по сайту: