 |
Вынужденные колебания при наличии трения
|
|
|
|
Исследование вынужденных колебаний при наличии трения вполне аналогично произведенному в п. 1.2 вынужденные колебания. Мы остановимся здесь подробно на представляющем самостоятельный интерес случае периодической вынуждающей силы.
Прибавив в правой стороне уравнения (4.1) внешнюю силу f cos yt и разделив на т, получим уравнение движения в виде
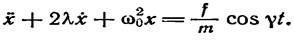 (5.1)
(5.1)
Решение этого уравнения удобно находить в комплексной форме, для чего пишем в правой части eiγt вместо cos yt:
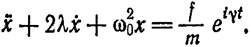
Частный интеграл ищем в виде x = B eiγt и находим для В:
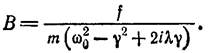 (5.2)
(5.2)
Представив В в виде beiδ, имеем для b и δ:
 (5.3)
(5.3)
Наконец, отделив вещественную часть от выражения Beiγt = bei (γt+δ), получим частный интеграл уравнения (5.1), а прибавив к нему общее решение уравнения без правой части (которое мы напишем для определенности для случая ω0>λ), получим окончательно:
х = ае -λt cos (ω t+ a) + b cos (γ t + δ). (5.4)
Первое слагаемое экспоненциально убывает со временем, так что через достаточно большой промежуток времени остается только второй член:
x = b cos (γ t + δ). (5.5)
Выражение (5.3) для амплитуды b вынужденного колебания хотя и возрастает при приближении частоты γ к ω0, но не обращается в бесконечность, как это было при резонансе в отсутствие трения. При заданной амплитуде силы f амплитуда колебания максимальна при частоте
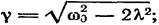
при λ<<<ω0 это значение отличается от ω0 лишь на величину второго порядка малости.
Рассмотрим область вблизи резонанса. Положим γ= ω0 + ε, где ε — малая величина; будем также считать, что λ<<ω 0. Тогда в (5.2) можно приближенно заменить:

так что
 (5.6)
(5.6)
или
|
|
|
 (5.7)
(5.7)
Отметим характерную особенность хода изменения разности фаз δ между колебанием и вынуждающей силой при изменении частоты последней. Эта разность всегда отрицательна, т. е. колебание «запаздывает» относительно внешней силы. Вдали от резонанса, со стороны γ< ω0, δ стремится к нулю, а со стороны γ > ω0 — к значению — π. Изменение δ от нуля до — π происходит в узкой (ширины ~ λ) области частот, близких к ω0; через значение -π/2 разность фаз проходит при γ = ω0. Отметим в этой связи, что в отсутствие трения изменение фазы вынужденного колебания на величину π происходит скачком при γ = ω0 (второй член в (2.4) меняет знак); учет трения «размазывает» этот скачок.
При установившемся движении, когда система совершает вынужденные колебания (5.5), ее энергия остается неизменной. В то же время система непрерывно поглощает (от источника внешней силы) энергию, которая диссипируется благодаря наличию трения. Обозначим посредством I (γ)количество энергии, поглощаемой в среднем в единицу времени, как функцию частоты внешней силы. Согласно (4.13) имеем: I (γ) = 2 F,
где F — среднее (по периоду колебания) значение диссипативной функции. Для одномерного движения выражение (4.11) диссипативной функции сводится к
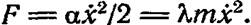
Подставив сюда (5.5), получим:

Среднее по времени значение квадрата синуса равно ½, поэтому
I (γ) = λ mb ²γ². (5.8)
Вблизи резонанса, подставляя амплитуду колебания из (5.7), имеем:
 (5.9)
(5.9)
Такой вид зависимости поглощения от частоты называется дисперсионным. Полушириной резонансной кривой (рис. 1)

называют значение |ε|, при котором величина I (ε) уменьшается вдвое по сравнению с ее максимальным значением при ε = 0.Из формулы (5.9) видно, что в данном случае эта полуширина совпадает с показателем затухания λ. Высота же максимума
I (0) = f ² / 4 mλ
|
|
|
обратно пропорциональна λ. Таким образом, при уменьшении показателя затухания резонансная кривая становится уже и выше, т. е. ее максимум становится более острым. Площадь же под резонансной кривой остается при этом неизменной. Последняя дается интегралом

Поскольку I (ε) быстро убывает при увеличении |ε|, так что область больших |ε| все равно не существенна, можно при интегрировании писать I (ε) в виде (5.9), а нижний предел заменить на — ∞. Тогда
 (5.10)
(5.10)
Заключение
Колебание — более или менее регулярно повторяющийся процесс. Таково очень нестрогое, «качественное» определение понятия «колебание». Можно привести множество примеров колебательных процессов, относящихся к различным областям физики (и не только физики). Колеблется маятник часов; колеблется груз, подвешенный на пружине. Колеблется взволнованная поверхность воды и гитарная струна. Колеблется заряд на пластинах конденсатора и магнитное поле в катушке индуктивности колебательного контура; периодически изменяется температура воздуха (зимой холоднее — летом теплее) и количество автомобилей на улицах города (больше в часы пик — меньше поздней ночью). Периодически меняется экономическая ситуация в жизни общества: кризисные явления сменяются подъемом экономики. Колеблется давление (или плотность воздуха), вызывая колебания ушной мембраны — и мы слышим голос певца на оперной сцене. Таких примеров можно привести как угодно много. Ознакомились с колебаниями в той или иной физической системе. Здесь же познакомились с наиболее часто встречающимися простейшими видами колебательных движений, основными характеристиками колебательных процессов, с математическим способом описания колебаний.
В результате проделанной работы было рассмотрено следующее:
― свободные одномерные колебания;
― вынужденные колебания;
― колебания систем со многими степенями свободы;
― затухающие колебания;
― вынужденные колебания при наличии трения.
Список использованной литературы:
1. Ландау Л.Д., Лифшнц Е.М. Теоретическая физика: Учеб. пособие. — Т.I. Механика. — 4-е изд., испр. — М.: Наука. 1988.— 216 с.
2. Кингсеп А.С, Локшин Г.Р., Ольхов О.А. Основы физики. Курс общей физики: Учебн. В 2 т. Т. 1. Механика, электричество и магнетизм, колебания и волны, волновая оптика — М.: ФИЗИАТЛИТ, 2001. ― 560 с.
|
|
|
3. Матвеев А.Н., Механика и теория относительности: Учеб. для студентов вузов / А.Н. Матвеев. — 3-е изд. — М.: ООО «Издательский дом «ОНИКС 21 век»: 000 «Издательство «Мир и Образование», 2003. — 432 с.
4. И.В.Савельев, Курс общей физики, том I. Механика, колебания и волны, молекулярная физика. М.: Издательство «Наука», 1970г.― 517с.
5. Зоммерфельд А., Механика. ― Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. ― 368 с.
|
|
|


