Краткие теоретические сведения.

В измерительной практике для повышения качества измерений часто обращаются к измерениям с многократными наблюдениями, т.е. к повторению одним и тем же оператором однократных наблюдений в одинаковых условиях, с использованием одного и того же средства измерений. В результате соответствующей обработки полученных данных удается уменьшить влияние случайной составляющей погрешности на результат измерений. При этом могут быть использованы различные процедуры обработки. В данной лабораторной работе кратко описана стандартная методика выполнения прямых измерений с многократными, независимыми наблюдениями и основные положения по обработке результатов наблюдений и оцениванию погрешностей результатов измерений. Эта методика соответствует рекомендациям действующего ГОСТ 8.207-76 «Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений».

При использовании данной методики руководствуются следующими правилами:

1. Проверку гипотезы о принадлежности результатов наблюдений нормальному распределению проводят с помощью критерия (Пирсона) с уровнем значимости , выбираемым в диапазоне от 0,01 до 0,1 (табл. 7).

Т а б л и ц а 7

Значения для -распределения

Кол-во степеней свободы	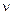Уровень значимости
0,01	0,05	0,1
	0,00016	0,00393	0,0158
	0,0201	0,103	0,211
	0,115	0,352	0,584
	0,297	0,711	1,06
	0,554	1,15	1,61
	0,872	1,64	2,2
	1,24	2,17	2,83
	1,65	2,73	3,49
	2,09	3,33	4,17
	2,56	3,94	4,87
	3,05	4,57	5,58
	3,57	5,23	6,3
	4,11	5,89	7,04
	4,66	6,57	7,79
	5,23	7,26	8,55

2. При определении доверительных границ погрешности результата измерения значение доверительной вероятности принимают равной 0,95.

3. В тех случаях, когда измерения нельзя повторить, помимо доверительных границ, соответствующих вероятности , допускается указывать границы для .

 

Вычисление среднего арифметического ряда наблюдений. Среднее арифметическое ряда наблюдений (результатов наблюдений) рассчитывают по формуле

,

где 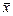– среднее арифметическое ряда наблюдений, – i -й результат наблюдения, – число результатов наблюдений.

 

Вычисление оценки среднего квадратического отклонения ряда наблюдений. Среднее квадратическое отклонение ряда наблюдений рассчитывают по формуле

.

Оно является основной характеристикой размера случайных погрешностей результатов наблюдений.

 

Вычисление среднего квадратического отклонения результата измерения. Для расчета среднего квадратического отклонения результата измерения используется формула

.

Проверка гипотезы о принадлежности результатов наблюдений нормальному распределению. Чтобы установить, принадлежат (или не принадлежат) результаты наблюдений тому или иному распределению, необходимо сравнить экспериментальную функцию распределения с предполагаемой теоретической. Сравнение осуществляется с помощью критериев согласия.

В случае проверки принадлежности результатов наблюдений к нормальному распределению предпочтительным, при числе результатов , является один из критериев: Пирсона или Мизеса – Смирнова. В настоящей работе используется критерий Пирсона.

При числе результатов наблюдений произво-
дят приближенную проверку их принадлежности к нормаль-
ному распределению путем оценки коэффициента асимметрии и эксцесса.

При гипотеза о принадлежности результатов наблюдений к какому-либо распределению не проверяется. Если при этом имеется априорная информация о том, что нет причин, которые могли бы вызвать заметное отклонение распределения результатов от нормального закона, для обработки результатов наблюдений используется распределение Стьюдента.

Для проверки принадлежности результатов наблюдений к нормальному распределению с помощью критерия согласия Пирсона необходимо сначала построить гистограмму.

Построение гистограммы включает в себя следующие этапы.

1. Результаты наблюдений располагаются в порядке возрастания: , ,…, , где .

2. Вычисляется диапазон изменения значений результатов наблюдений: .

3. Весь этот диапазон разбивается на интервалов одинаковой ширины. Необходимое количество интервалов разбиения можно оценить по формуле

(1)

с последующим округлением в большую сторону до ближайшего целого нечетного числа (обычно лежит в диапазоне от 7 до 15).

4. Определяется ширина интервала: .

5. Определяются границы интервалов так, чтобы верхняя граница j -го интервала 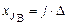, а нижняя граница совпадала с верхней границей (j -1)-го интервала: .

6. Для каждого j -го интервала (j = 1,2,..., ) вычисляются числа 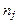– частость попадания результата наблюдений в j -й интервал.

7. Строится гистограмма. Для этого по оси результатов наблюдений в порядке возрастания номеров откладываются интервалы и на каждом интервале строится прямоугольник, высота которого пропорциональна .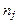

По результатам анализа гистограммы высказывается гипотеза о виде закона распределения экспериментальных данных и о численных характеристиках этого закона (для нормального распределения такими характеристиками являются математическое ожидание и дисперсия). После этого используют критерий согласия для проверки гипотезы.

Критерий согласия Пирсона имеет вид [2]

,

где величина характеризует меру отклонения результатов наблюдений от теоретически предсказанных, 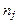– частость попадания результатов наблюдений в j -й интервал, – теоретические значения вероятности попадания результатов в j -й интервал, которые вычисляются по формуле

,

где – функция Лапласа, , а .

После вычисления значения для заданного уровня значимости и числа степеней свободы 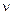по таблицам -распре-деления находят критическое значение критерия согласия . Число степеней свободы рассчитывают по формуле

, (2)

где – количество интервалов разбиения, 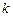– число параметров, необходимых для определения теоретической функции распределения (для нормального закона распределения ).

В технической практике обычно задаются уровнем значимости = 0,05. Значения для этого уровня значимости приведены в табл. 7.

Если , то принимают гипотезу о том, что результаты наблюдений принадлежат нормальному распределению, характеризующемуся математическим ожиданием и дисперсией. В противном случае, если , гипотеза отвергается.

Вычисление доверительных границ случайной погрешности результата измерения. Доверительные границы случайной погрешности результата измерения (без учета знака) находят по формуле

,

где – квантиль распределения Стьюдента, который зависит от доверительной вероятности 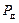и числа наблюдений . Значения величины приведены в табл. 8.

 

Т а б л и ц а 8

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: