 |
Статика МОВ (Поверхностная Совместимая статика)
|
|
|
|
На этом важном этапе обработки трассы каждого (или возможно большего количества) бина суммируются, чтобы сформировать стабильную и представительную пилотную трассу (одна пилотная трасса для каждого бина ОСТ). Перекрестная корреляция отдельных трасс с пилотными трассами определит значения сдвига по времени, применяемые к каждой трассе. Матричные расчеты разделяют статпоправки для каждого положения ПП и ПВ – в целом называемые поверхностно-совместимое решение.
Стыковка статики (Виггинс, и пр., 1976) применяет то условие, что каждое положение ПП возбуждается многими ПВ и наоборот. Методы перекрестной корреляции определяют временные различия между соседними ПП и соседними ПВ. Эти временные различия при умножении на инверсию геометрической матрицы представляют значения статики (поверхностно-совместимой) на каждом положении ПП и ПВ. Если инверсия геометрии имеет «дырки», тогда статика не будет определена для определенных пространственных длин волн. (Мы рассматриваем абсолютные статические значения, разложенные на сумму различных пространственных длин волн).
Под «дырками» мы обычно подразумеваем, что матрицы геометрии не определены (т.е. уравнения не могут определить статику для некоторых ПВ и ПП), или, другими словами, уравнения присутствуют, но слишком малы, чтобы преодолеть потенциальные ошибки выбора (Рис. 10.7). «Уравнения» происходят от существующих пар ПП – ПВ.

Рис. 10.8
Рисунок 10.8 иллюстрирует различные пары ПП – ПВ, принадлежащие различным бинам ОСТ. Этот прямолинейный пример демонстрирует, что, если ПВ 1, 5, 9,... принадлежат одному бину ОСТ, тогда ПВ 2, 6, 10,... принадлежат следующему бину ОСТ и ПВ 3, 7, 11... – последующему бину. Это означает, что когда мы запишем все уравнения для каждой пары ПВ – ПП, не будет уравнений, связывающих статику взрывов для ПВ 1,скажем, для ПВ 2 (то же значит и для ПВ 3 и ПВ 4). В основном, в этом случае, мы имеем 4 семейства уравнения, которые не связаны друг с другом.
|
|
|
Теперь известно (Вайскап Р. Д., 1994), что все обычно пространственные прямолинейные геометрии (кирпичные, зигзагом, и т.д.) не стыкуются в статике (т.е. существует более одного независимого решения для статики ПВ и ПП). В кирпичном проектировании, например, ПП непременно стыкуются, в то время, как ПВ все еще не состыкованы. ПВ все еще не состыкованы из-за правильной геометрии ПП. В проектировании Флекси-бина все ПВ и ПП состыкованы (кроме расположенных по краям съемки) из-за неповторяющейся природы соответственных положений ПВ и ПП и пересечений линий. Чтобы связать независимые решения вместе, Вайскап предполагает использование сглаживания в структурных условиях. Обычно это дает разумные решения (без поперечного «дрожания»), но могут оставаться ошибки в статике длинных длин волн, если таковые присутствуют, и структурная аномалия (которая зачастую и есть то, что мы ищем!) может решаться неадекватно.

Рис. 10.9
Стыковка статики может гарантироваться распадением правильности геометрии (Рис. 10.9, напр., неравномерное расстояние между линиями и ПВ или ПП) или добавлением линий ПВ и ПП в направлении линий ПП и линий ПП в направлении линий ПВ.
Следует особо отметить, что геометрия, которая хороша для статики, может быть плоха для изображения. Другими словами, мы должны быть очень внимательными и помнить, что то, что мы ищем – это подповерхностное 3D изображение, которое не является околоповерхностным изображением (которое нам дает статика). Следовательно, всегда необходимо идти на компромисс в пользу подповерхностных целей.
Используйте компьютерную программу для проверки каждой расстилки.
|
|
|
DMO
В то время как НМО корректирует задержку по времени на трассе выноса с помощью передвижения амплитуд вдоль трасс, ДМО сдвигает данные вверх по падению до правильного положения, где трасса нулевого выноса записывала бы отражатель падения (Рис. 10.10). Затем миграция перемещает энергию на правильное горизонтальное и вертикальное подповерхностное положение.

Рис. 10.10
ДМО – приложение специфичное для падений в частичной миграции до суммы, за которой следует НМО и суммирование. Гейл (1984) детально обсуждал процесс. Постоянная скорость НМО – наиболее применяемый метод. Меняющееся во времени ДМО было описано Менардусом и Шлейчером (1991) среди прочих.
Эллипс ДМО имел наибольший эффект на данные при мелких временах и на дальних выносах. Изменение поверхностной геометрии может представить аномалии амплитуд из-за различных смешений выносов и азимутов, которые могут или не могут компенсироваться в обработке.
3D ДМО требует как можно больше выносов в каждом диапазоне выносов, чтобы сформировать отражения с помощью предполагаемой интерференции. В противном случае, происходит усиление несовершенных изображений. Эта конструкция сечений выносов может быть сложной в 3D съемках из-за рассеивания СТ и вариаций азимутов ПВ – ПП. Следовательно, не все проекты 3D приведут к удачному применению ДМО.
Пусть вынос ПВ – ПП будет h, средняя скорость – V и время целевого горизонта – t (Рис. 10.11). Тогда энергия во время “t” в бине ОСТ извлекается из пар ПВ – ПП, которые пересекают бин, и чьи СТ находятся в h2/(2 x V x t) бина (Дережовский, геофизическая разведка, 1982, стр. 318). Кратность и число отдельных выносов в каждом бине после ДМО на каком-то определенном времени “t” – хорошее измерение реакции ДМО.

Рис. 10.11
Пример: V = 3000 м/с h = 1000 м t = 1,0 с
Радиус ДМО = h2 / (2Vt) = 170 м
Или около 7 бинов, если b = 25 м
Или: V = 10000 фт/с h = 3000 фт t = 1,0 с
Радиус ДМО = h2 / (2Vt) = 450 фт
Или около 4 бинов, если b = 110 фт
Другими словами, все трассы:
- чей вынос равен 1000 м (3000 фт),
- чей азимут ПВ – ПП проходит через центральный бин,
- чья СТ расположена в 170 м (450 фт) от того центрального бина,
будут каждая передавать энергию центральному бину.
Заметьте, что 5-градусный отражатель падения будет иметь свою энергию, повернутую по горизонтали на расстояние равное h2 / V x t) x sinθ x cosθ, или, используя значения V, h, t, указанные выше, мы получим 15 м.
|
|
|
Центральная выборка на Рис. 10.12 создается из многих других трасс, делающих вклад в выборки. Чем дальше расположена трасса от центральной, тем круче энергия падения, которую они буду передавать центральному дискрету. Предполагаемая интерференция гарантирует, что падения будут изображены на истинном положении их нулевого выноса, а не на положении ОСТ. Затем будет правильно произведено суммирование на каждой ОСТ (потому что каждая трасса содержит информацию по нулевому выносу). Миграция после суммы затем передвинет падения на их истинное геологическое положение (ОГТ). Если трассы утеряны, предполагаемая интерференция нарушается, это обычно происходит из-за отпечатывания геометрии.
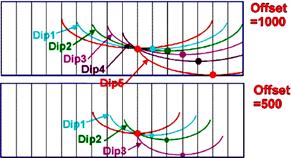
Рис. 10.12
Плохое проектирование геометрии может создать «дырки» в «плоскости» выносов и нехватка определенных выносов в правильном образце может затруднять процесс предполагаемой интерференции для определенных падений.
Балансировка бинов. Этот метод обработки стал весьма популярен последние лет десять. Он компенсируется для бинов, которые не имеют хорошего смешения посредством «заимствования» пропущенного выноса у соседних бинов – на деле, вид смешения или интерполяции для определенных трасс. Очень важно отметить, что этот вид «заимствования бинов» - это как раз то, что выполняет ДМО. Таким образом, если ДМО включено в последовательность сейсмической обработки, не должно быть требований по балансировке/заимствованию бинов.
Хорошее измерение «усиливающей интерференции» ДМО должно рассчитать взвешенную кратность ДМО (Кроузи и Пион, 1993) в каждом бине для определенного целевого времени и скорости. Эта «взвешенная кратность ДМО» строится посредством рассмотрения всех возможных передач энергии одному выходному бину ОСТ. Энергия от многих пар ПВ – ПП, чьи оси пересекают этот бин, будет «смазываться» ДМО и приходить в заданный выходной бин. Энергия будет сильнее или слабее, в зависимости от того, как далеко она уходила вдоль оператора (эллипса) ДМО. Функции взвешивания известны и позволяют нам рассчитать взвешенную сумму всех передач энергии для любого данного бина.
|
|
|
На Рис. 10.3 мы рассчитали эту взвешенную кратность ДМО для истинной 3D геометрии с рекой в центре (белые крестики в центре показывают пропущенные приемники). Пронаблюдайте площади большой и малой кратности из-за несомненной передачи энергии дальних выносов, присутствующих в бинах близко к препятствию – в данном, случае, к реке. Такие вариации во взвешенной кратности ДМО могут привести к аномалиям в данных из-за вариаций Сигнал/шум, которые отражают (как в зеркале) кратность.


Рис. 10.13
В дополнение к аномалиям кратности ДМО, которые могут выводить отпечатывание геометрии, как показано выше, мы рассчитали реакцию ДМО для падений, записанных с различными геометриями. Эти реакции показывают серьезные изменения фазы и амплитуды, указывающие, что такие цели падения, если таковые присутствуют, в реальных данных показали бы сильный отпечаток геометрии (Коннелли и Галбрейт, 1995).

Рис. 10.14
В этом исследовании «цель» - это псевдопадение, где предполагается, что каждый бин ОСТ имеет специфичное падение в специфичное время и азимут, как изображено на Рис. 10.14.
Расчет заключается в помещении передачи энергии каждой пары ПВ – ПП на псевдо-падение, в специфичное целевое время, в каждом бине по всей съемке. Идеальная реакция нулевой фазы указала бы, что объект будет полностью отображен с помощью ДМО в этом бине: т.е. что процесс усиливающей интерференции работает. Менее идеальная реакция указывает на недостаточное количество передач энергии на то падение в том бине.
На Рис. 10.15 мы видим результат применения алгоритма к стандартной «кирпичной» геометрии. Продольное расстояние между ЛПП и ЛПВ – 50 м. Интервал между линиями ПВ и ПП – 400 м. Заплатка – 4 линии по 80 пунктов в каждой, истинная кратность ОСТ = 10. Мы показываем результат в одной «ячейке» съемки для угла падения – 30 градусов в направлении СВ (т.е. ориентирован на 45 градусов на каждую ячейку) и при времени – 0,4 с. В трех направлениях три реакции соответствуют 19 бинам ОСТ:
1. вдоль линии ПВ;
2. вдоль линии ПП;
3. вдоль диагонали ячейки;(Рис. 10.15d)
Имеются значительные амплитудные и фазовые изменения, указывающие на то, что выход ДМО, примененного к истинным сейсмическим данным, собранным с использованием данной геометрии, будет иметь сильный «отпечаток геометрии» для всех 30 – градусных падений в северо-восточном направлении, по времени близких к 0,4 сек.
|
|
|
Наши примеры с отличной геометрией и, следовательно, кратностью показывают похожие результаты – в общем, всегда хуже для более крутых падений на малых временах и значительно хуже для падений поперек узких заплаток, указывая на истинную нужду в:
либо (а) расчете некоторой формы амплитудной и фазовой компенсации (обратный оператор ДМО,
либо (б) перепроектировании геометрии сбора данных, чтобы улучшить переход энергии на выходе ДМО во всех бинах для желаемого целевого падения и времени. Не используйте узкие заплатки для применения ДМО.
Хотя подобные изучения значительно использовали ДМО, похоже, что прочие методики изображения (напр., время до суммы или глубинна миграция) пострадают от тех же самых проблем – иначе говоря, недостаточные переходы энергии, приводящие к плохо сфокусированным изображениям.
 a
a
 b
b
 c
c
 d
d
Рис. 10.15.
Сумма
Суммирование ОСТ суммирует трассы в бинах ОСТ с видом на увеличение Сигнал/Шум.
Вопрос «Что такое кратность?» пестрит проблемами. Существует ли хорошая кратность и плохая кратность? (См. Рис. 10.16).
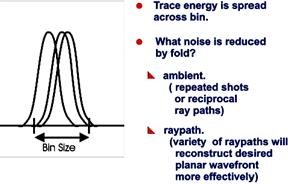
Рис. 10.16
Например, какой вид шума затухает с помощью многократного повторения ПВ на один и тот же ПП? В данном случае, очевидно, что будут затухать шумы ОС (или фоновые), включая влияния от инструментальных шумов. Но получим ли мы улучшенный сигнал? Если мы стреляем взаимообратные трассы луча – те же поверхностные положения, но, меняя местами ПВ и ПП – многие могут оспорить, что это равно тому же, что и повторное отстреливание одного и того же пункта взрыва. Эти случаи могут быть свободно классифицированы как «плохая кратность».
С другой стороны, что если мы скомбинируем трассы, чья энергия проходит по нескольким различным трассам луча? Комбинация таких энергий фронта волны может считаться грубой версией суммирования вторичного импульса по Хьюджену. Такая ситуация может легко классифицироваться как «хорошая кратность».
Если в каждом бине ОСТ присутствует хорошее смешение выносов, это не только вызовет затухание случайного шума, но еще и когерентного шума, такого, как шум от источника или энергии кратных волн, из-за присутствия такого шума в различное время на различных выносах. Если, тем не менее, нет хорошего смешения выносов, кратные волны и шум от источника и прочие когерентные шумы будут присутствовать на суммированных трассах ОСТ.
На Рисунке 10.17 мы показали синтетический взрыв с тремя объектами на глубине – 200 мсек, 500 мсек и 1000 мсек. Имеется сильный линейный шум со скоростью – 800 м/с. Если мы используем геометрию некоторых ОГТ истинной 3D, мы можем сконструировать синтетический сбор ОСТ данных с трассами в каждом бине, определенными трассами этого взрыва, которые имеют тот же вынос. Другими словами, наша модель плоская, и шум одинаков везде.

Рис. 10.17
На Рисунке 10.18 мы видим синтетические сборы ОСТ. Совершенно очевидно, что линейный шум теперь выглядит несколько нерегулярным из-за неправильного смешения выносов в каждом бине ОСТ.

Рис. 10.18
Когда это выборки ОСТ обработаны с помощью НМО и суммированы, шум не снижен. Более того, он затухает в различных направлениях, в зависимости от смешения выносов в различных бинах. На Рисунке 10.19, бины вдоль линии ПВ и вдоль линии ПП. Абсолютно очевидно, что исходный линейный шум присутствует в сумме, что может интерпретироваться, как истинные данные, в зависимости от направления, в котором мы смотрим.
|
|
|


