 |
Коэффициент корреляции и его свойства
|
|
|
|
Мера зависимости между вариационными рядами характеризуется коэффициентом корреляции. Для линейной корреляционной зависимости угловые коэффициенты прямых регрессии выражаются через коэффициент корреляции, который определяется по формуле Пирсона:
 ,
,
где 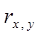 - коэффициент корреляции
- коэффициент корреляции
хi, yi – значения параметров в i -том наблюдении
n – число наблюдений
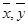 - средние значения параметров х и у для n проведённых
- средние значения параметров х и у для n проведённых
наблюдений.
или:
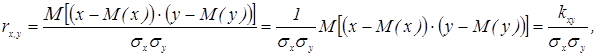
где  - генеральные средние квадратические отклонения,
- генеральные средние квадратические отклонения,
kх,у - называется корреляционным моментом или ковариацией.
Коэффициент корреляции показывает долю рассеяния величины х под влиянием у (и наоборот).
СВОЙСТВА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Величина коэффициента корреляции всегда заключена в пределах:

1. Если r<0, то с увеличением в вариационном ряду наблюдаемых значений х соответствующие им значения у вариационного ряда уменьшаются.
2. Если r>0, то с увеличением одного параметра другой параметр в среднем возрастает.
3. Если r=0, то параметры х и у абсолютно независимы друг от друга.
4. Если r=1, то между параметрами х и у существует прямо пропорциональная функциональная зависимость.
5. Чем больше по абсолютной величине 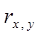 , тем сильнее проявляется связь между х и у, тем ближе эта зависимость к функциональной и тем значительнее влияние х ( или у ) на у (или х) среди всех других влияющих факторов.
, тем сильнее проявляется связь между х и у, тем ближе эта зависимость к функциональной и тем значительнее влияние х ( или у ) на у (или х) среди всех других влияющих факторов.
6. Чем больше абсолютная величина 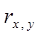 , тем больше доверительная вероятность того, что характер этой связи действительно соответствует полученному коэффициентному корреляции.
, тем больше доверительная вероятность того, что характер этой связи действительно соответствует полученному коэффициентному корреляции.
Принято считать, что связь между исследуемыми параметрами или явлениями:
а) слабая при 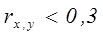
б) средняя при 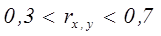
в) тесная при 
|
|
|
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ ЛИНЕЙНОЙ ЗАВИСИМОСТИ
Для экспериментального изучения зависимости между двумя величинами х и у производят некоторое количество n независимых испытаний:
х1, х2,...,хn
y1, y2,...,yn
Результат i -того измерения дает пару значений xi, yi ( i =1,2,…..n).
Вычисления производят в следующем порядке:
- Вычисляют выборочные средние:


- Вычисляют выборочные средние квадратические отклонения:

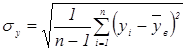
- Вычисляют оценку ковариации.
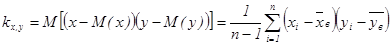
- Вычисляют коэффициент корреляции
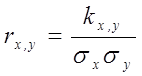
Эталоны решения типовых задач
Задача 1. Рассчитать коэффициент парной линейной корреляционной зависимости, сделать вывод по знаку коэффициента корреляции и о степени связи следующих величин.
| Объем крови х i (л) | 4,22 | 4,69 | 5,04 | 4,34 | 4,22 | 4,8 | 4,45 | 4,69 | 4,92 | 4,57 |
| Вес у i, (кг) |
Решение. Определим выборочные средние:

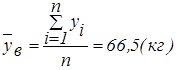
Составим таблицу:
| S | |||||||||||
 (л) (л)
| -0,37 | 0,1 | 0,45 | -0,25 | -0,37 | 0,21 | -0,14 | 0,1 | 0,33 | -0,02 | |
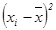 (л2) (л2)
| 0,14 | 0,01 | 0,20 | 0,06 | 0,14 | 0,04 | 0,02 | 0,01 | 0,11 | 0,0004 | 0,73 |
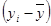 (кг) (кг)
| -14,5 | 6,5 | 19,5 | -12,5 | -16,5 | 7,5 | -5,5 | 2,5 | 13,5 | -0,5 | |
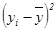 (кг2) (кг2)
| 210,25 | 42,25 | 380,25 | 156,25 | 272,25 | 56,25 | 30,25 | 6,25 | 182,25 | 0,25 | 1336,5 |
 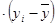 (л,кг) (л,кг)
| 5,36 | 0,65 | 8,77 | 3,125 | 6,10 | 1,57 | 0,77 | 0,25 | 4,45 | 0,01 | 31,05 |
Вычислим выборочные среднеквадратические отклонения:
 (л)
(л)
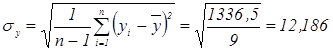 (кг)
(кг)
Вычислим оценку ковариации:
 (л, кг)
(л, кг)
Вычислим коэффициент корреляции:
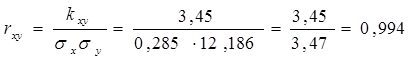
Вывод: С увеличением веса человека объем циркулирующей крови увеличивается, причем связь между этими параметрами является сильной.
Задача 2. Рассчитать коэффициент парной корреляционной зависимости, сделать вывод по знаку коэффициента корреляции, о степени связи между величинами, построить корреляционное поле и провести линию регрессии:
| Основной обмен веществ хi (%) | ||||||||||
| Амплитуда артериального давление уi (мм рт.ст.) |
Решение
Вычислим выборочные средние 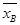 и
и  :
:
|
|
|
 =
= 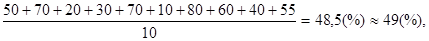
 =
=  (мм рт.ст)
(мм рт.ст)
Заполним таблицу:
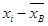 (%) (%)
| -29 | -19 | -39 | -9 | ||||||||
 (%)2 (%)2
| 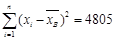
| |||||||||||
 (мм рт.ст.) (мм рт.ст.)
| -2 | -22 | -12 | -32 | -7 | |||||||
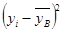 (мм рт.ст.)2 (мм рт.ст.)2
| 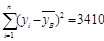
| |||||||||||
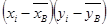 (%, мм рт.ст.)
(%, мм рт.ст.)
| -2 | 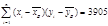
|
Вычислим выборочные средние квадратичные отклонения σх и σу:

 =
= 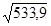 =23,11(%),
=23,11(%),
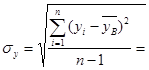
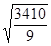 =
=  ≈19,47 (мм.рт.ст)
≈19,47 (мм.рт.ст)
Вычислим оценку ковариации kх,у:
kх,у 
Вычисляем коэффициент корреляции rx,y:
rx,y= 
Построим корреляционное поле и проведем линию регрессии:

Вывод: Связь между основным обменом веществ (%) и амплитудой артериального давления (мм рт. ст) очень тесная, так как, rx,y>0,7 и с увеличением основного обмена амплитуда артериального давления растет (почти прямо пропорциональная зависимость, так как rx,y ≈1).
Задача 2. Рассчитать коэффициент корреляции при атеросклерозе между площадью поражений артерий таза (%) и возрастом больного. Сделать вывод о связи исследуемых величин.
| n=8 | |||||||||
| х (%) | 22,3 | 3,1 | 48,3 | 17,0 | 7,5 | 40,2 | 23,1 | 16,0 | 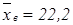
|
| у (годы) | 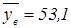
| ||||||||
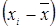 (%) (%)
| 0,1 | -1,91 | 26,1 | -5,2 | -14,7 | 0,9 | -6,2 | ||
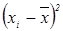 (%)2 (%)2
| 0,01 | 364,8 | 681,2 | 216,1 | 0,81 | 38,4 | ∑=1652,3 | ||
 (год) (год)
| 1,9 | -21,1 | 21,9 | -3,1 | -8,1 | 11,9 | 1,9 | -8,1 | |
 (год)2 (год)2
| 3,6 | 445,2 | 4,796 | 9,6 | 65,6 | 141,6 | 3,6 | 65,6 | ∑=1214,4 |
 (%, год) (%, год)
| 0,2 | 571,6 | 16,1 | 119,1 | 214,2 | 1,71 | 50,2 | ∑=1376,1 |
Вычислим выборочные среднеквадратические отклонения:
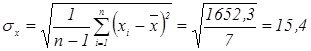 (%),
(%),
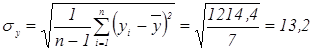 (год).
(год).
Вычислим оценку ковариации:
 (%, год).
(%, год).
Вычислим коэффициент корреляции:
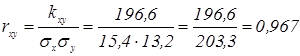 .
.
Вывод: С увеличением возраста больного атеросклерозом площадь поражений артерий таза увеличивается. Связь между этими параметрами является сильной.
ПРАКТИЧЕСКАЯ ЧАСТЬ
|
|
|


