 |
Пример расчета коэффициента корреляции Пирсона.
|
|
|
|
Допустим, что в результате лечения 12 больных с артериальной гипертензией в результате суточного мониторирования систолического артериального давления (САД) до лечения и после месячного лечения были получены следующие результаты:
| № | САД до ( ) )
| САД после (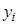 ) )
| 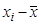
| 
| 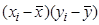
|
| -9,6 | -7,5 | ||||
| -19,6 | -17,5 | ||||
| -14,6 | -12,5 | 182,5 | |||
| -4,6 | 7,5 | -34,5 | |||
| 0,4 | 12,5 | ||||
| 5,4 | 12,5 | 67,5 | |||
| -9,6 | -7,5 | ||||
| 10,4 | 7,5 | ||||
| 15,4 | 12,5 | 192,5 | |||
| 0,4 | -7,5 | -3 | |||
| 5,4 | -2,5 | -13,5 | |||
| 20,4 | 2,5 | ||||

| 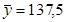
| 
| |||
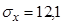
| 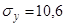
|

Итак, коэффициент корреляции получился равным 0,718.
Определим, достоверно ли он отличается от нуля. Для этого используем Таблицу 10 приложения. У нас 12 пар измерений, поэтому входим в Таблицу по 12 строке. На пересечении 12 строки и столбца Р=0,05 стоит число 0,576. Полученный коэффициент корреляции (0,718) больше этого числа. Следовательно, на этом уровне коэффициент корреляции достоверно отличается от нуля, то есть связь есть. На пересечении этой же строки и столбца Р=0,01 стоит число 0,708. Поскольку коэффициент корреляции больше и этого числа, следовательно, мы можем говорить, что связь существует и на этом более значимом уровне. Итак, ответ на первый вопрос таков: существование связи высоко достоверно. Далее, поскольку получено положительное значение коэффициента корреляции, мы заключаем, что связь прямая. Используя Таблицу 2 данного раздела, мы приходим к заключению, что связь сильная.
Найдем коэффициент детерминации:
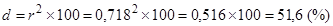
Таким образом, систолическое артериальное давление после лечения на 51,6 % определяется систолическим артериальным давлением до лечения, а на 48,4 % другими факторами.
|
|
|
Рекомендуемая литература:
- Лобоцкая Н.Л. Основы высшей математики. Минск: Вышэйшая школа, 1973. - 352 с.
- Урбах В.Ю. Статистический анализ в биологических и медицинских исследованиях М: Медицина - 1975 - 297 с.
- Лакин Г.Ф. Биометрия. М: Высшая школа -1980 - 291 с.
- Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. М., МедиаСфера, 2002. 312 с.
- Петри А., Сэбин К. Наглядная статистика в медицине. М., Издательский дом Геотар-Мед.,2003. 143 с.
- Флетчер Р., Флетчер С., Вагнер Э. Клиническая эпидемиология. М., МедиаСфера, 1998. 352 с.
- Власов В.В. Эпидемиология. М., Издательский дом Геотар-Мед., 2004. 462 с.
ПРИЛОЖЕНИЕ 1
Таблица основных формул дифференцирования функций
1. 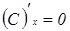
2. 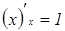
3. 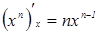
4. 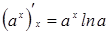
5. 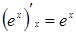
6. 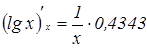
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
ПРИЛОЖЕНИЕ 2
Правила дифференцирования сложных функций
1. 
2. 
3. 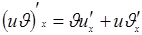
4. 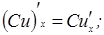
5. 
6. 
7. 
8. 
9. 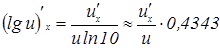
10. 
11. 

12. 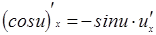

13. 
14. 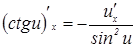
15. 
16. 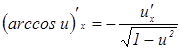
17. 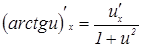
18. 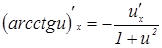 .
.
ПРИЛОЖЕНИЕ 3
Основные формулы интегрирования
1. 
2. 
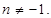
3. 
4. 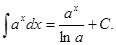
5. 
6. 
7. 
8. 
9. 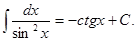
10. 
11. 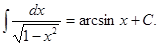
12. 
13. 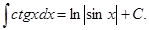
14. 
15. 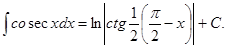
16. 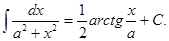
17. 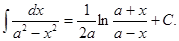
18. 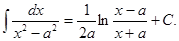
19. 
20. 
21. 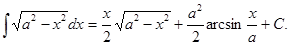
22. 
23. 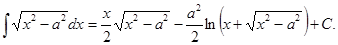
24. 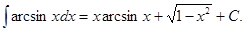
25. 
26. 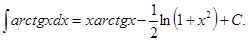
27. 
28. 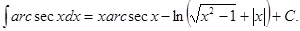
29. 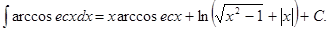
ПРИЛОЖЕНИЕ 4
Значения функции распределения нормированной нормально распределенной случайной величины 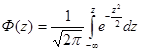
| z | ||||||||||
| 0,0 0,5000 0,5040 0,5080 0,5120 0,5160 0,5199 0,5239 0,5279 0,5319 0,5359 0,1 5398 5438 5478 5517 5557 5596 5536 5675 5714 5753 0,2 5793 5832 5871 5910 5948 5987 6026 6064 6103 6141 0,3 6179 6217 6255 6293 6331 6368 6406 6443 6480 6517 0,4 6554 6591 6628 6664 6700 6736 6772 6808 6879 6879 0,5 0,6915 0,6950 0,6985 0,7019 0,7054 0,7088 0,7123 0,7157 0,7190 0,7224 0,6 7257 7291 7324 7357 7389 7422 7454 7486 7517 7549 0,7 7580 7611 7642 7673 7704 7734 7764 7794 7823 7852 0,8 7881 7910 7939 7967 7995 8023 8051 8078 8106 8189 0,9 8159 8186 8212 8238 8264 8289 8315 8340 8365 8389 1,0 0,8413 0,8438 0,8461 0,8485 0,8508 0,8531 0,8554 0,8577 0,8599 0,8621 1,1 8643 8665 8686 8708 8729 8749 8770 8790 8810 8830 1,2 8849 8869 8888 8907 8925 8944 8963 8980 8997 9015 1,3 9032 9049 9066 9082 9099 9115 9131 9147 9162 9167 1,4 9192 9207 9222 9236 9251 9265 9279 9292 9306 9319 1,5 0,9332 0,9345 0,9357 0,9370 0,9382 0,9394 0,9406 0,9418 0,9429 0,9441 1,6 9452 9463 9474 9484 9495 9505 9515 9525 9535 9545 1,7 9554 9564 9573 9582 9591 9599 9608 9616 9625 9633 1,8 9641 9649 9656 9664 9671 9678 9686 9693 9699 9706 1,9 9713 9719 9726 9732 9738 9744 9750 9756 9761 9767 2,0 0,9772 0,9778 0,9783 0,9788 0,9793 0,9798 0,9803 0,9808 0,9812 0,9817 2,1 9821 9826 9830 9834 9838 9842 9846 9850 9854 9857 2,2 9861 9864 9868 9871 9875 9878 9881 9884 9887 9890 2,3 9893 9896 9898 9901 9904 9906 9909 9911 9913 9916 2,4 9918 9920 9922 9925 9927 9929 9931 9932 9934 9936 2,5 0,9938 0,9940 0,9941 0,9943 0,9945 0,9946 0,9948 0,9949 0,9951 0,9952 2,6 9953 9955 9956 9957 9959 9960 9961 9962 9963 9964 2,7 9965 9965 9967 9968 9969 9970 9971 9972 9973 9974 2,8 9974 9975 9976 9977 9977 9978 9979 9979 9980 9981 2,9 9981 9982 9982 9983 9984 9984 9985 9985 9986 9986 3,0 0,9987 0,9987 0,9987 0,9988 0,9988 0,9989 0,9989 0,9989 0,9990 0,9990 3,1 9990 9991 9991 9991 9992 9992 9992 9992 9993 9993 3,2 9993 9994 9994 9994 9994 9994 9994 9995 9995 9995 3,3 9995 9995 9995 9996 9996 9996 9996 9996 9996 9997 3,4 9997 9997 9997 9997 9997 9997 9997 9997 9997 9998 |
|
|
|
ПРИЛОЖЕНИЕ 5
Значения коэффициента Стьюдента t.
| P n-1 | 0,95 | 0,99 | 0,999 | P n-1 | 0,95 | 0,99 | 0,999 |
| 1 12,706 63,657 636,619 18 2,103 2,878 3,992 2 4,303 9,925 31,598 19 2,093 2,861 3,883 3 3,182 5,841 12,941 20 2,086 2,845 3,850 4 2,776 4,604 8,610 21 2,080 2,831 3,819 5 2,571 4,032 6,859 22 2,074 2,819 3,792 6 2,447 3,707 5,959 23 2,069 2,807 3,767 7 2,365 3,499 5,405 24 2,064 2,797 3,745 8 2,306 3,355 5,041 25 2,060 2,787 3,725 9 2,262 3,250 4,781 26 2,056 2,779 3,707 10 2,228 3,169 4,587 27 2,052 2,771 3,690 11 2,201 3,106 4,487 28 2,048 2,763 3,674 12 2,179 3,055 4,318 29 2,045 2,756 3,659 13 2,160 3,012 4,221 30 2,042 2,750 3,646 14 2,145 2,977 4,140 40 2,021 2,704 3,551 15 2,131 2,947 4,073 60 2,000 2,660 3,460 16 2,120 2,921 4,015 120 1,980 2,617 3,374 17 2,110 2,898 3,965 ¥ 1,960 2,576 3,291 |
ПРИЛОЖЕНИЕ 6
Тригонометрические функции суммы и разности углов, кратных и половинных углов
1.  6.
6. 
2.  7.
7. 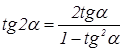 .
.
3. 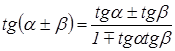 . 8.
. 8. 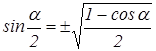 .
.
4.  9.
9. 
5.  10.
10. 
ПРИЛОЖЕНИЕ 7
Произведения и степени тригонометрических функций
1. 
2. 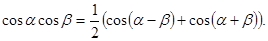
3. 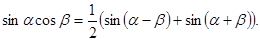
4. 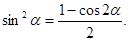
5. 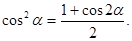
6. 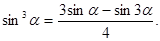
7. 
ПРИЛОЖЕНИЕ 8
Некоторые часто встречающиеся величины
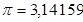 .
. 
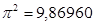
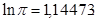

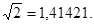
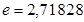
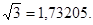

 рад.
рад.

 рад.
рад.
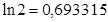
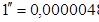 рад.
рад.
ПРИЛОЖЕНИЕ 9
Значения тригонометрических функций для углов, кратных  и
и  (
(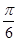 и
и  )
)
| Функция | Углы | ||||||
| 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
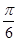
| 
| 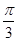
| 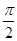
| 
| 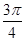
| 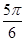
| |
sin 0 1/2 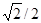  1 1   1/2
cos 1 1/2
cos 1 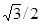  1/2 0 -1/2 - 1/2 0 -1/2 -  - -  tg 0
tg 0 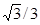 1 1  ±¥ - ±¥ -  -1 - -1 - 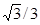 ctg
ctg   1 1 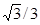 0 - 0 - 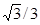 -1 - -1 -  sec 1 2
sec 1 2 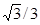 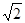 2 ±¥ -2 - 2 ±¥ -2 - 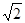 -2 -2 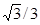 cosec
cosec  2 2 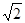 2 2 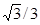 1 2 1 2 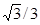 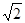 2 2
|
| Функция | Углы | |||||||
| 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
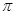
| 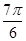
| 
| 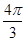
| 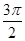
| 
| 
| 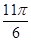
| 
|
sin 0 -1/2 - 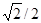 - -  -1 - -1 -   -1/2 0
cos -1 - -1/2 0
cos -1 -  - - 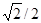 -1/2 0 1/2 -1/2 0 1/2  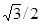 1
tg 0 1
tg 0 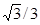 1 1  ±¥ - ±¥ -  -1 - -1 - 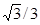 0
ctg 0
ctg   1 1 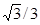 0 - 0 - 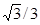 -1 - -1 -   sec -1 -2
sec -1 -2 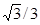 - - 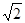 -2 -2  2 2 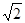 -2 -2 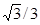 1
cosec ±¥ -2 - 1
cosec ±¥ -2 - 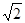 -2 -2 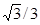 -1 -2 -1 -2 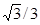 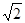 -2 -2 
|
ПРИЛОЖЕНИЯ 10
Коэффициент корреляции Пирсона. Определение достоверности отличия от нуля.

|
|
|


