 |
Вращательные движения НМС направлены
|
|
|
|
в разные стороны и w1¹w2
Точка D вращается только относительно оси О2z, двигаясь со скоростью VD=w2×BD, направленной в плоскости сечения перпендикулярно ВD (рис. 82).
Точка В вращается только относительно оси О1z, двигаясь со скоростью VВ=w1×BD, направленной в плоскости сечения перпендикулярно BD в ту же сторону, что и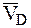 
(рис. 82).
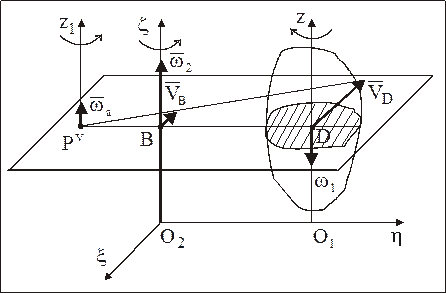
Рис. 82
Используя третий способ нахождения мгновенного центра скоростей (рис. 33) и для определенности полагая, что w2>w1, определим его положение — точку Pv (рис. 82).
Проделав операции аналогичные проделанным в случае, рассмотренным в п. 8.4.1, получим:
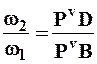(8.9)
и
(8.10)
(при выводе формулы (8.9) также используется свойство пропорции только для разности числителей и знаменателей).
Если НМС вращается одновременно относительно двух параллельных осей в разные стороны с различными по модулю угловыми скоростям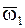и 
и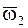 
, то абсолютное движение НМС будет мгновенным вращательным с абсолютной угловой скоростью 
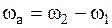вокруг мгновенной оси, параллельной данным. Положение оси определяется пропорцией (8.9). Абсолютная угловая скорость 
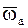направлена в сторону большей угловой скорости.
Вращательные движения НМС направлены
в разные стороны и w1=w2 (пара вращений)
Как и в предыдущем случае, рассмотренном в п. 8.4.2., VВ=w1×BD и VD=w2×BD, с той лишь разницей, что VВ = VD, так как w1=w2.
Используя четвертый способ нахождения мгновенного центра скоростей (рис. 34), определим, что он находится в бесконечности, т. е. абсолютное движение НМС является мгновенным поступательным движением, а все ее МТ в данный момент времени имеют одинаковые скорости V=w1×BD=w2×BD. Из (8.10) также следует, что абсолютная угловая скорость НМС в этом случае равна нулю:
|
|
|
Рис. 83
Если НМС вращается одновременно относительно двух параллельных осей в разные стороны с равными по модулю угловыми скоростями 
= 
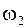(пара вращений), то абсолютное движение НМС будет мгновенным поступательным со скоростью V=w1×BD=w1×BD, где BD — расстояние между осями, называемое плечом пары вращений.
Из того, что пара вращений НМС эквивалентна поступательному движению НМС, следует и обратное: поступательное движение НМС эквивалентно паре вращений НМС.
Примером пары вращений НМС может служить движение педали велосипеда относительно рамы.
Сложение поступательного и вращательного
Движений НМС
Пусть НМС вращается с угловой скоростью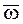 
относительно оси Oz, которая, в свою очередь, вместе с НМС перемещается поступательно со скоростью 
относительно неподвижной системы координат O1xhz (рис. 84 – 87).
В зависимости от угла a между векторами 
и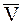 
возможны три случая.
8.5.1. Скорость поступательного движения перпендикулярна оси вращательного движения НМС (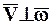
)
Сложное движение НМС, совершаемое в этом случае, состоит из переносного поступательного движения и относительного вращательного движения НМС и представляет собой плоскопараллельное движение НМС (глава 4) по отношению к плоскости zОh, перпендикулярной к оси вращения Oz (ось Оx направлена по направлению 
).
Для нахождения абсолютного движения НМС заменим поступательное движение НМС со скоростью парой вращений 
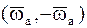, расположенной в плоскости, перпендикулярной к , причем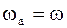 
, а плечо пары ОO1=V/w (рис. 84).
Вращения с угловыми скоростям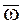и 
и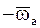 
, как имеющие общую ось Оz и равные модули угловых скоростей, взаимно уничтожаются и, следовательно, абсолютное движение НМС есть мгновенное вращательное движение НМС с угловой скоростью 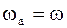относительно оси Oz¢ (рис. 84).
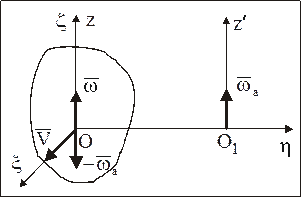
Рис. 84
Если НМС участвует в поступательном движении со скоростью 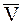и во вращательном движении с угловой скоростью , которая направлена перпендикулярно к , то абсолютное движение НМС будет мгновенным вращательным движением вокруг мгновенной оси, параллельной оси данного вращения и отстоящей от нее на расстоянии, равном V/w. При этом абсолютная угловая скорость 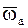НМС равна по модулю и направлению данной угловой скорости 
.
|
|
|
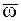8.5.2. Скорость поступательного движения параллельна оси вращательного движения НМС (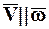
)
Определение: Cложное движение НМС, при котором скорость поступательного движения НМС (переносное движение) параллельна угловой скорости вращательного движения НМС (относительное движение), называется винтовым движением НМС (рис. 85).
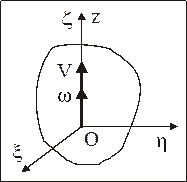
Рис. 85
При этом ось вращения НМС Oz называется винтовой осью. Если вектора 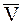и направлены в одну сторону, то винт называется правым, если в разные стороны — то левым.
Расстояние, проходимое вдоль оси винта за время одного оборота любой точкой НМС, не лежащей на оси винта, называется шагом h винта.
Траектория любой точки НМС, не лежащей на оси винта, при постоянном шаге винта расположена на поверхности круглого цилиндра и называется винтовой линией (рис. 86).
Скорость МТ, находящейся от оси винта на расстоянии r, определяется формулой:
.
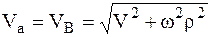и направлена по касательной к траектории винтовой линии (рис. 86).
Рис. 86
Шаг винта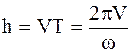 
, здесь время Т определяется из соотношения 2p=Тw, т.е. 
.
|
|
|
