 |
Скорость поступательного движения образует с осью вращательного движения НМС произвольный угол
|
|
|
|
Сложное движение в этом случае состоит из переносного поступательного движения и относительного вращательного движения НМС и представляет собой общий случай движения НМС (глава 6).
Для нахождения абсолютного движения НМС разложим вектор 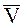 в плоскости xОz, положение которой определяется векторами
в плоскости xОz, положение которой определяется векторами 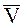 и
и  , на составляющие, направленные по оси вращения и перпендикулярно к ней (рис. 87):
, на составляющие, направленные по оси вращения и перпендикулярно к ней (рис. 87):
Используя случай 8.5.1 для 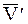 и
и  , получим мгновенное вращательное движение вокруг мгновенной оси О1z', параллельной оси Oz и отстоящей от нее на расстоянии
, получим мгновенное вращательное движение вокруг мгновенной оси О1z', параллельной оси Oz и отстоящей от нее на расстоянии 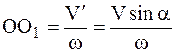 . При этом угловая скорость
. При этом угловая скорость  НМС равна по модулю и направлению данной угловой скорости
НМС равна по модулю и направлению данной угловой скорости 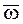 .
.
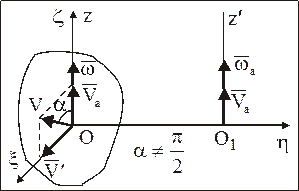
Рис. 87
Так как составляющая 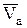 скорости поступательного движения НМС является свободным вектором, то ее можно перенести параллельно самой себе в точку О1 и, таким образом, в точке О1 получим случай, рассмотренный в п. 8.5.2,
скорости поступательного движения НМС является свободным вектором, то ее можно перенести параллельно самой себе в точку О1 и, таким образом, в точке О1 получим случай, рассмотренный в п. 8.5.2, 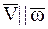 .
.
Если НМС участвует в поступательном движении со скоростью 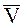 и во вращательном движении с угловой скоростью
и во вращательном движении с угловой скоростью  , образующей произвольный угол
, образующей произвольный угол 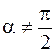 со скоростью
со скоростью 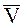 , то абсолютное движение НМС будет мгновенным винтовым движением со скоростью поступательного движения
, то абсолютное движение НМС будет мгновенным винтовым движением со скоростью поступательного движения  и угловой скоростью
и угловой скоростью 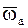 , равной по модулю и направлению данной угловой скорости
, равной по модулю и направлению данной угловой скорости 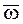 , с мгновенной винтовой осью, параллельной оси данного вращения и отстоящей от нее на расстоянии, равном
, с мгновенной винтовой осью, параллельной оси данного вращения и отстоящей от нее на расстоянии, равном  .
.
Теорема: Совокупность движений НМС, определяемых мгновенной угловой скоростью  и поступательной скоростью
и поступательной скоростью 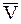 , направленной не перпендикулярно к
, направленной не перпендикулярно к  , сводится к мгновенному винтовому движению около мгновенной винтовой оси.
, сводится к мгновенному винтовому движению около мгновенной винтовой оси.
Сложное движение НМС в этом случае совпадает с общим случаем движения НМС (глава 6) и может быть представлено в виде последовательных мгновенных винтовых движений относительно винтовых осей, положение которых будет непрерывно меняться.
|
|
|
Заключение
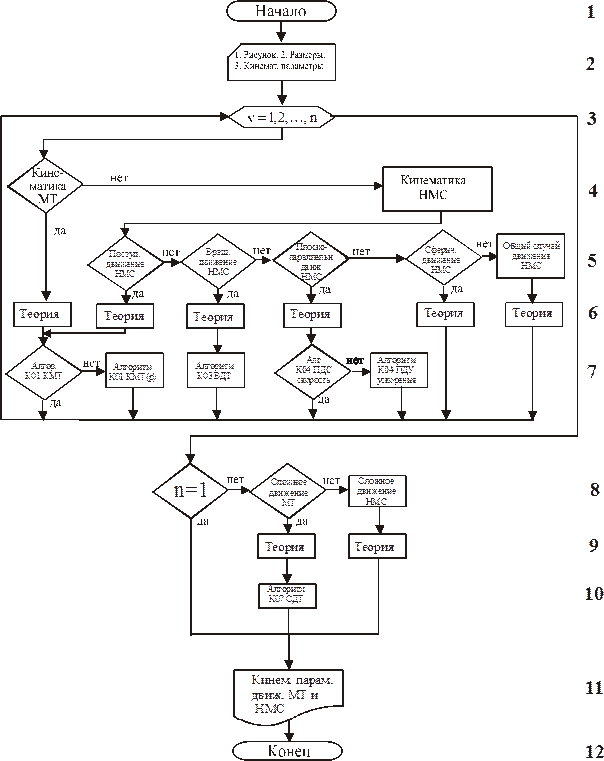
Алгоритм кинематики – управляющий – К00 УПР
С комментариями
Комментарии
| К.2.Принимаются рассматриваемые объекты за МТ, СМТ, МС, НМС, АТТ. Определяется подход к рассматриваемому движению как к одному или к нескольким движениям (сложное движение). |
| К.3,8.Здесь n – число движений МТ и НМС, случай n>1 соответствует сложному движению МТ и НМС. |
| К.4.Рассматриваются способы задания и кинематические параметры движения МТ. |
К.5-7.Определяется тип движения НМС. Поступательное и вращательное движения НМС (главы 2, 3) являются ее простейшими движениями. Плоскопараллельное (глава 4), сферическое (глава 5) и общий случай движения НМС (глава 6) могут быть рассмотрены как одно движение, а могут быть рассмотрены как сложные движения НМС, состоящие из ее простейших движений:
· плоскопараллельное движение – мгновенное вращательное движение относительно мгновенного центра скоростей или сочетание поступательного и вращательного движений НМС;
· сферическое движение – мгновенное вращательное движение относительно мгновенной оси вращения, проходящей через неподвижную точку или сочетание трех вращательных движений НМС;
· общий случай движения – мгновенное вращательное движение относительно перемещающейся мгновенной оси вращения или сочетание поступательного и сферического движений НМС.
В кинематике НМС:
· угловые скорость 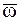 и ускорение и ускорение  (кроме случая поступательного движения НМС, для которого (кроме случая поступательного движения НМС, для которого 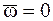 и и  ) в каждый момент времени одинаковы для всех МТ, принадлежащих НМС, т. е. являются кинематическими параметрами всего НМС;
· скорости ) в каждый момент времени одинаковы для всех МТ, принадлежащих НМС, т. е. являются кинематическими параметрами всего НМС;
· скорости 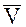 и ускорения и ускорения 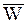 МТ, принадлежащих НМС зависят от положения этих МТ в НМС, т. е. являются кинематическими параметрами этих МТ.
К6. Следует отметить динамику изменения угловой скорости при различных видах движений:
· при поступательном движении НМС угловая скорость НМС равна нулю;
· при вращательном движении НМС относительно неподвижной оси угловая скорость направлена по неподвижной оси вращения;
· при плоско-параллельном движении НМС угловая скорость перпендикулярна плоскости сечения НМС и перемещается параллельно самой себе;
· при движении НМС с одной неподвижной точкой угловая скорость меняет направление, всегда проходя через неподвижную точку;
· при движении НМС в общем случае угловая скорость перемещается вместе с полюсом и меняет направление, всегда проходя через полюс.
Т. е. по существу рассмотрены все виды движения НМС, включающие все возможные случаи изменения направления угловой скорости. МТ, принадлежащих НМС зависят от положения этих МТ в НМС, т. е. являются кинематическими параметрами этих МТ.
К6. Следует отметить динамику изменения угловой скорости при различных видах движений:
· при поступательном движении НМС угловая скорость НМС равна нулю;
· при вращательном движении НМС относительно неподвижной оси угловая скорость направлена по неподвижной оси вращения;
· при плоско-параллельном движении НМС угловая скорость перпендикулярна плоскости сечения НМС и перемещается параллельно самой себе;
· при движении НМС с одной неподвижной точкой угловая скорость меняет направление, всегда проходя через неподвижную точку;
· при движении НМС в общем случае угловая скорость перемещается вместе с полюсом и меняет направление, всегда проходя через полюс.
Т. е. по существу рассмотрены все виды движения НМС, включающие все возможные случаи изменения направления угловой скорости.
|
| К.8-10.Используется при рассмотрении сложного движения МТ (глава 7) один из разделов кинематики НМС (движения подвижной системы координат, связанной с каким-либо НМС, относительно неподвижной системы координат – переносное движение) и кинематики МТ (движение МТ относительно этой НМС – относительное движение). Сложное движение НМС (глава 8) включает в себя различные случаи сочетаний движения НМС. |
Примечание
|
|
|
Так как кинематика механических движений НМС по существу сводится к рассмотрению или поступательного, или вращательного движений, или комбинаций этих движений НМС, то следует ожидать, что и причинами, вызывающими эти движения, должны быть такие параметры, измеряющие меру механических взаимодействий объектов, как сила и пара сил или их комбинации (Ч. 2 Статика).
|
|
|


