 |
Поиск оптимального решения
|
|
|
|
ПО СКАЛЯРНОМУ (СВЕРНУТОМУ) КРИТЕРИЮ
В дальнейшем, не снижая общности, будем обозначать сверткувекторного критерия в скаляр как U=U(Wn)=U(w1,w2...wn).
В этом случае, под наилучшим будем понимать решение, обеспечивающее максимальное значение обобщенного показателя U=U(Wn). Тогда задача поиска оптимального решения может быть записана следующим образом:
Необходимо найти такое решение x = x° (xÎX), которое обращает показатель обобщенный показатель эффективности операции U в максимум
U° (x°) = мах U(Wn(x))
xÎX
Принципиальным отличием данной задачи от традиционных задач математического программирования является то, что значение целевой функции U(x) вычисляется не напрямую, а через модель исследуемой системы W = W(x) и функцию свертки U= U(Wn), т.е. U(Wn(x)). Это приводит к тому, что вид целевой функции (выпуклая, монотонная, многоэкстремальная), как и области решения по оптимизируемым переменным Х (выпуклая, невыпуклая) априорно неизвестен. Поэтому для поиска экстремума необходимо использовать численные методы оптимизации, допускающие решение задачи в широком классе целевых функций и ограничений.
МЕТОД «ВЗВЕШЕННОЙ СУММЫ»
B этом случае обобщенный показатель U представляется в виде суммы показателей с весовыми коэффициентами ai, которые отражают ценность i-ого показателя (его важность для обобщенного показателя) по сравнению с остальными.
n
U =å ai ui
i=1
Весовые коэффициенты ai представляют в этом случае компоненты вектора градиента целевой функции. Поиск решения сводится к задаче оптимизации с целевой функцией, линейной относительно компонент векторного критерия Wn(w1,w2...wn), но не вектора Х. Наилучшим будет решение, расположенное максимально далеко в критериальном пространстве от начала координат в направлении градиента (см. рис.).
|
|
|

Альтернатива 2 оптимальна по взвешенной сумме
МЕТОД ИДЕАЛЬНОЙ ТОЧКИ.
В этом случае обобщенный показатель U=U(Wn)=U(w1,w2...wn) вычисляется как расстояние (длина вектора) в критериальном пространстве между точкой с текущими координатами Wn=U(w1,w2...wn) и точкой (идеальной), координаты которой задаются ЛПР (экспертом) Wnид =U(w1ид,w2ид...wnид). Как правило, такое решение (идеальное), в общем случае может не существовать, т.е. не реализуемо.
Значение целевой функции U(x) вычисляется также не напрямую, а через модель исследуемой системы и функцию свертки, т.е. U(Wn(x)).
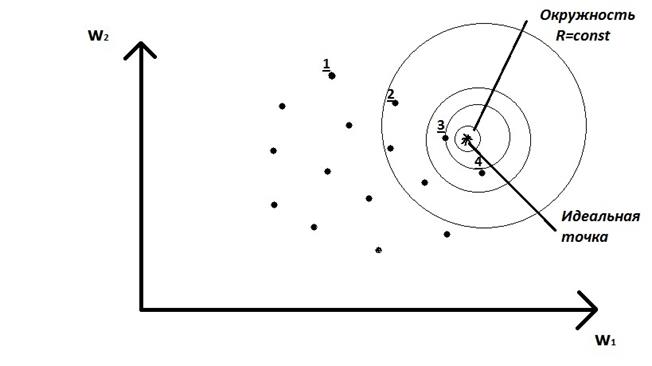
Т.3, ближайшая по расстоянию до идеальной точки
ПОИСК ПО ПОЛЕЗНОСТИ (ПРЕДПОЧТЕНИЯМ)
Полезность часто задаётся ЛПР (или экспертом) в виде функции полезности – некоторой функции вида U=F (Wn)= F (w1,w2...wn), отражающей «полезность» получаемых решений с его точки зрения (формализованная свертка). Вид функции полезности обычно выбирается из заданного класса функций в евклидовом пространстве.
Как было сказано выше, полезность может быть задана в критериальном пространстве в виде функции полезности (ФП) U=F (Wn)= F (w1,w2...wn), отражающей «полезность» получаемых решений с точки зрения ЛПР.

Точка 3 наилучшая по полезности
Аналогично и предпочтения также являются индивидуальной оценкой качества альтернатив, определяемой ЛПР и отображают его систему ценностей (предпочтений) на множестве альтернатив.
Для задания предпочтений (в отличие от полезности) используется качественная (лексическая) шкала, на которой значения задаются в виде некоторых высказываний (термов), упорядоченных по предпочтению в порядке возрастания (убывания).

1-недопустимо
2-плохо
3-удвлетворительно
4-хорошо
5-отлично
Т.т. 14,15-«плохо»
Т.т.1,2,4,5,6,11-«удвлетворительно»
|
|
|
Т.т.7,8,3,9,12,13-«хорошо»
Т.10-«отлично»
Следует заметить, что при использовании методов, связанных с сопоставлением различных альтернатив по какой-либо компоненте векторного критерия понятие лучше (больше), в общем случае, не является монотонной функцией своего аргумента (напр. Температура воды для плавания в бассейне).
Основные достоинства и недостатки различных методов скаляризации векторного критерия.
Критерий среднего взвешенного. Достоинства
1. Простота формализации
2. Ясный физический смысл
3. Учет индивидуальных представлений ЛПР о задаче при назначении весовых коэффициентов (важностей)
4. Наличие простой формальной процедуры (метод парных сравнений), облегчающей процесс назначения весовых коэффициентов
Недостатки:
1. Неявная взаимная компенсация показателей, которая становится неконтролируемой при большом их числе.
Не учет нелинейной зависимости весовых коэффициентов от значений показателей: важности вводятся один раз и остаются постоянными величинами.
Метод идеальной точки. Достоинства:
1. Компоненты векторного критерия рассматриваются в совокупности (без применения сверток)
2. Четкая формальная постановка
Недостатки:
1. Неявная взаимная компенсация показателей, которая становится неконтролируемой при большом их числе.
2. Произвольный выбор метрики
3. Непредставимость, в содержательном смысле, расстояния между двумя точками в n-мерном пространстве (при n>3).
Метод последовательных уступок. Достоинства:
1. Содержательная простота
2. Учет всех компонент векторного критерия
Недостатки:
1. Необходимость предварительного ранжирования показателей по важности
2 Трудность определения величин уступок
3. Практическая не реализуемость при большом числе показателей
Оптимальность по Парето. Достоинства:
1. Метод математически строг и понятен пользователю.
2. Выделяет множество допустимых решений.,
3. Дает возможность ЛПР сосредоточить анализ решений на более узком множестве и выбрать субъективно оптимальное решение.
Недостатки:
1. Применимость метода ограничена мощностью Парето-оптимального множества (для непосредственного выбора решения количество его элементов не должно превышать 7-10). Если у недоминируемого множества большая мощность, то метод трудно выполним без привлечения одного из рассмотренных выше способов.
|
|
|
Свертка по полезности, свертка по предпочтениям. Хотя оба метода можно рассматривать как способ скаляризации векторного критерия, по существу это способы выявления неформальной информации, которой обладает ЛПР. Информации основанной на знаниях, опыте, интуиции и сложившейся на этой основе системе ценностей ЛПР. Внешне они просты для пользователя, однако это далеко не так. Выявление и формализация системы ценностей ЛПР, выражаемой в виде предпочтений или полезностей требует организации достаточно сложных процедур. Одна из таких процедур будет рассмотрена ниже на примере СППР DSS/UTES. (см. лекции по ИО Бомас В.В.).
|
|
|


