 |
Решение задачи о рассеянии в общем случае
|
|
|
|
КУРСОВАЯ РАБОТА
На тему:
"Рассеяние волн в задаче о маскировке объектов методом волнового обтекания"
Минск, 2010 г.
Введение
У людей с давних времён есть желание замаскироваться, а то и вовсе стать невидимым для окружающих. И с недавних пор это может стать возможным с помощью метода волнового обтекания. Основной целью курсовой работы является изучение метода рассеяния волн в задаче о маскировке объектов методом волнового обтекания, рассмотрение основных характеристик и свойств маскирующих покрытий, изучение их классификации. А также, как дополнение, рассмотрение быстрого преобразования Фурье и его применения в задаче о рассеянии. Задача курсовой работы заключается в овладении методом решения задачи о рассеянии и изучении маскирующих оболочек.
Под маскировкой или скрытием методом волнового обтекания следует понимать такое преобразование фронта волны маскирующей оболочкой, что он огибает скрываемый объект. В реальных условиях невозможно добиться идеальной маскировки, но принципиально возможно сведение потерь и рассеяния к пренебрежимо малым для поставленной задачи значением. А в задаче маскировки таких сравнительно небольших объектов, как тело человека, ракет, самолётов, и прочей военной техники, учитывая маловероятность отклика радаров на большое для идеальных моделей, но значительно меньшее, чем у объектов без маскирующих оболочек, рассеяние, при желании распределённое во всех направлениях, делает их скрытие очень перспективной и востребованной задачей. Учитывая характер явления, его преимущественной областью применения является военно-стратегическая.
|
|
|
Решение задачи о рассеянии
Решение задачи о рассеянии в общем случае
В общем случае задача о рассеянии ставится следующим образом. На некоторый объект произвольной формы с диэлектрической проницаемостью 
и объемом V падает электромагнитная волна в направлении распространения 
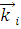и с колебаниями электрического вектора в направлении 
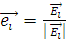(рис. 1.1). Волна движется в пространстве с диэлектрической проницаемостью 
. После рассеивания и поглощения результирующая волна имеет направление распространения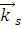 
и колебания электрического вектора в направлении 
.
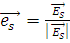Для вычисления рассеянных электромагнитных полей и сечения рассеяния необходимо сначала записать общее решение для поля внутри рассеивающего тела, поля рассеянных волн и падающего поля, а затем вычислить неизвестные постоянные коэффициенты (спектральные амплитуды) с помощью граничных условий.
Решение задачи о рассеянии в общем случае
Решение задачи о рассеянии в общем случае заключается в нахождении сечения рассеяния.
Запишем электрическое поле падающей волны следующим образом:
, (1.2.1)
где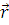 
= 
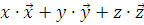– вектор описывающие местоположение относительно базиса (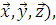
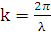– волновое число. Рассеянное поле вдали от рассеивателя может быть описано сферической волной:
, (1.2.2)
где r – расстояние от рассматриваемой точки до точки рассеяния,
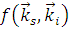– амплитуда рассеяния, зависящая от направления рассеянной 
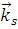и падающей 
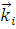волн.
Магнитное поле падающей волны вычисляется из уравнений Максвелла и имеет следующий вид:
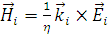, (1.2.3)
где η=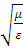 
есть волновое сопротивление (импеданс).
Вектор Умова-Пойтинга, который определяет поток мощности поля через единицу поверхности, записывается следующим образом:
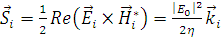. (1.2.4)
Рассуждаем так же и для рассеянной волны. Магнитное поле рассеянной волны по определению следующее
, (1.2.5)
а вектор Умова-Пойтинга рассеянной волны
|
|
|
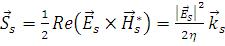, 1.2.6.
Подставляя выражение (1.2.2) в (1.2.6), получаем
. (1.2.7)
В сферической системе координат возьмём дифференциал телесного угла в направлении рассеяния (рис 1.2)
. (1.2.8)
На расстоянии r, от рассеивающей точки, площадь поверхности ограниченной дифференциалом телесного угла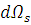 
записывается следующим образом:
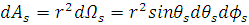. (1.2.9)
Тогда дифференциал рассеянной мощности через площадку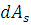 
принимает следующий вид:
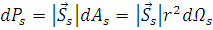. (1.2.10)
Дифференциал телесного угла в сферических координатах r, θs, φs
Теперь, подставляя (1.2.7) в (1.2.10) получим следующее выражение для мощности, рассеянной в элемент телесного угла:
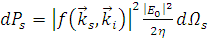. (1.2.11)
Разделив левую и правую части выражения (1.2.11) на вектор Умова-Пойтинга для падающей волны (1.2.4), получим
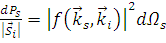. (1.2.12)
Размерность последнего соотношения является размерностью площади.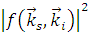 
называется дифференциальным сечением рассеяния и обозначается как 
.
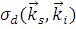А интегрирование 1.2.12, в свою очередь, даёт
. (1.2.13)
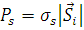, (1.2.14)
где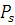 
– рассеянная мощность, а 
– сечение рассеяния.
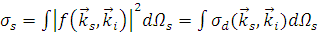. (1.2.15)
|
|
|
