Определение мест фактического обрыва нижних стержней

В целях экономии арматурной стали часть продольной рабочей арматуры обрывают в пролете, не доводя до опоры. Для определения мест обрыва строится эпюра материалов (арматуры). Места теоретического обрыва стержней определим графическим способом на огибающей эпюре изгибающих моментов (Рис. 4.2.).

 

М_s^пр=А_s^пр*R_s*u*h₀*10^-3=1206.4*365*0.922*0.65*10^-3=263.93 кН*м,

 

где u=1-0,5*x=1-0,5*0.156=0.922;

 

x=A_s^пр*R_s/R_b*b_р*h₀=1206.4*365/13.05*300*650=0.156.

 

Продольные стержни доводимые за край опоры: 3Æ16 (А_s1=603.2 мм²).

 

М_s1=А_s1*R_s*u*h₀*10^-3=603.2*365*0.961*0.65*10^-3=137.53 кН*м;

 

где u=1-0,5*x=1-0,5*0.078=0.961;

 

x=A_s1*R_s/R_b*b_р*h₀=603.2*365/13.05*300*650=0.078.

 

Определим расстояние от точек теоретического обрыва W из условий (здесь q_sw=A_sw*R_sw/S, d_s- диаметр обрываемого стержня):

 

W≥Q/(2*q_sw)+5*d_s,

если Q/(2*q_sw)>h₀, то W≥2*h₀*(1-q_sw*h₀/Q)+5*d_s,

 

W кратно 50 мм.

1) q_sw1=A_sw1*R_sw/S₁=150.8*285/200=214.885 кН/м,

Q₁/(2*q_sw1)+5*d_s=170.89/(2*214.885)+5*16=477.6 мм.

2*h₀*(1-q_sw1*h₀/Q₁)+5*d_s=2*650*(1-214.885*0.65/170.89)+5*16=317.5 мм.

Q₁/(2*q_sw1)=397.6<h₀.

 

Принимаем W₁=500 мм.

 

2) q_sw2=A_sw2*R_sw/S₂=150.8*285/200=214.885 кН/м,

Q₂/(2*q_sw2)+5*d_s.обр=168.58/(2*214.885)+5*16=472.3

2*h₀*(1-q_sw2*h₀/Q₂)+5*d_s=2*650*(1-214.885*0.65/168.58)+5*16=302.9 мм.

Q₂/(2*q_sw2)=392.3<h₀.

 

Принимаем W₂=500 мм.

Длина обрываемых нижних стержней (в пролетной части ригеля):

 

l_низ=l_1Т+W₁+W₂=2750+500+500=3750 мм.

 

Определение мест фактического обрыва верхних стержней

 

М_s^оп=А_s^оп*R_s*u*h₀*10^-3=2045.2*365*0.866*0.64*10^-3=413.70 кН*м,

 

где u=1-0,5*x=1-0,5*0.268=0.866;

 

x=A_s^оп*R_s/R_b*b_р*h₀=2045.2*365/13.05*300*640=0.268.

 

Продольные стержни доводимые за край опоры 4 (А_s2=436.7 мм²).

 

М_s2=А_s2*R_s*u*h₀*10^-3=436.7*365*0.971*0.64*10^-3=99.09 кН*м;

где u=1-0,5*x=1-0,5*0.057=0.971;

 

x=A_s2*R_s/R_b*b_р*h₀=436.7*365/13.05*300*640=0.057.

3) q_sw3=A_sw3*R_sw/S₁=150.8*285/200=214.885 кН/м.

Q₃/(2*q_sw3)+5*d_s.обр=296.15/(2*214.885)+5*0=689.1 мм.

2*h₀*(1-q_sw3*h₀/Q₃)+5*d_s=2*640*(1-214.885*0.64/Q₃)+5*0=685.6 мм.

Q₃/(2*q_sw3)>h_0.

 

Принимаем W₃=700 мм.

 

q_sw4=A_sw4*R_sw/S₁=150.8*285/200=214.885 кН/м.

Q₄/(2*q_sw4)+5*d_s.обр=243.89/(2*214.885)+5*0=567.5 мм.

2*h₀*(1-q_sw4*h₀/Q₄)+5*d_s=2*640*(1-214.885*0.64/243.89)+5*0=558.2 мм.

Q₄/(2*q_sw4)<h₀.

 

Принимаем W₄=600 мм.

Длина обрываемых верхних стержней:

- со стороны крайней колонны

 

l_{верх кр}=l_{2Т кр}+W₃=760+700=1460 мм, принимаем l_{верх кр}=1800 мм.

- со стороны средней колонны

 

l_{верх ср}=l_{2Т ср}+W₄=1200+600=1800 мм, принимаем l_{верх ср}=1800 мм.

Рис. 4.2. Эпюра материалов.

 

Рис. 4.3. Плоские каркасы ригеля перекрытия КР3 и КР4.

Проектирование колонны

Расчет колонны на устойчивость и прочность

 

Значение изгибающих моментов и продольных усилий принимается по результатам статического расчета поперечной рамы. Колонны принимаются двухэтажной разрезки. Колонны многоэтажного каркасного здания с жесткими узлами рассматриваются как элементы поперечной рамы и рассчитываются как внецентренно сжатые элементы от совместного действия изгибающих моментов и продольных сил.

Рассматривается нижняя колонна крайнего ряда сечением b_col*h_сol=400*400 мм, изготавливаемая из тяжелого бетона класса B30: g_b2=0.9; R_b=17 МПа; R_bt=1.2 МПа; (с учетом g_b2 R_b=15.3 МПа; R_bt=1.08 МПа), R_b,ser=22 МПа; R_bt,ser=1.8 МПа; E_b=29000 МПа, бетон подвергнут тепловой обработке, и арматуры класса A400 R_sc=365 МПа, R_s=365 МПа, E_s=200000 МПа.

Расчетная высота колонны принимается равной высоте этажа, т.е. l₀=3.3 м.

Максимальный изгибающий момент в ригеле M_max=370.04 кН*м, тогда получим одну комбинацию расчетных усилий в колонне:

М=0.6*M_max=0.6*370.04=222.024 кН*м,

N=2431.352 кН.

e₀=М/N=222.024/2431.352=0.0913 м.

Расчетные усилия от длительной нагрузки:

 

М_l=М*k_l=222.024*0.591=131.199 кН*м,

N_l=N*k_l=2431.352*0.591=1436.746 кН,

 

где k_l=(g^пер-8.4)/g^пер=(20.534-8.4)/20.534=0.591.

М₁=М+0,5*N*(h₀-a_sс)=222.024+0,5*2431.352*(0.36-0.04)=611.040 кН*м.

M_1l=М_l+0,5*N_l*(h₀-a_sс)=131.199+0,5*1436.746*(0.36-0.04)=361.079 кН*м.

α=E_s/E_b=200000/29000=6.897.

δ_e=e₀/h_col=0.0913/0.4=0.228>0.15=> примем δ_e=0.228.

φ_l=1+M_1l/M₁=1+361.079/611.040=1.591.

В первом приближении принимаем коэффициент армирования μ=0.033.

Определим жесткость

 

=

 

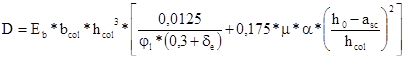=29000*0.4*0.4³*[0,0125/(1.591*(0,3+0.228))+

+0,175*0.033*6.897*((0.36-0.04)/0.4)²]=29.965 МПа*м⁴.

N_cr=π²*D/l₀²=π²*29.965/3.3²=27157.190 кН.

η_v=1/(1-N/N_cr)=1/(1-2431.352/27157.190)=1.098

M=M*η_v=222.024*1.098=243.856 кН*м.

α_m1=(M+N*(h₀-a_sc)/2)/(R_b*b*h₀²)=

=(243.856+2431.352*(0.36-0.04)/2)/(15.3*10³*0.4*0.36²)=0.798

δ₁=a_s/h₀=0.04/0.36=0.111

α_n=N/(R_b*b_соl*h₀)=2431.352/(15.3*10³*0.4*0.36)=1.104

ξ_R=0.531

α_n=1.104>ξ_R=0.531

 

Расчет ведем для случая α_n>ξ_R.

 

ξ₁=(α_n+ξ_R)/2=(1.104+0.531)/2=0.817

α_s=(α_m1-ξ₁*(1-ξ₁/2))/(1-δ₁)=(0.111-0.817*(1-0.817/2))/(1-0.111)=0.354

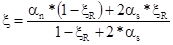=(1.104*(1-0.531)+2*0.354*0.531)/(1-0.531+2*0.354)=0.759

=

=15.3*10⁶*0.4*0.36*(0.111-0.759*(1-0.759/2))/(365*(1-0.111))=2220.0 мм².

 

Принимаем продольную арматуру колонны 3Æ32 A400 (A_s=A_sc=2412.7 мм²).

Конструктивные требования

Коэффициент армирования

 

μ₁=(A_s+A_sc)/(b_col*h₀)=(2412.7+2412.7)/(400*360)=

0.03351

 

μ₁>μ_min=0.001

I(μ-μ₁)/μI=I(0.033-0.03351)/0.033I=0.015<0,05

Диаметр поперечных стержней примем конструктивно из условий:

d_sw≥0.25*d_{s max} (условие свариваемости),

d_sw≥5 мм.

Максимальный диаметр d_{s max}=32 мм.

d_sw≥0.25*32=8 мм.

Примем d_sw=8 мм.

Шаг поперечных стержней примем конструктивно из условий:

S≤15*d_{s max}=15*32=480 мм,

S≤300 мм

Примем S=300 мм.

Принимаем поперечную арматуру колонны диметром d_sw=8 мм, с шагом S=300 мм, из арматуры класса A400.

Рис. 5.1. Схема армирования колонны.

Расчет консоли колонны

 

Рассчитывается консоль колонны крайнего ряда.

Максимальная опорная реакция ригеля: Q=390.53 кН.

 

l_sup=Q/(R_b*b_p)=390.53/(15.3*0.3)=85.08 мм.

 

Принимаем вылет консоли l=300 мм.

a=l-0.5*l_sup=300-0.5*85.08=257.5 мм.

Высота консоли в сечении у грани колонны h=600 мм.

Высота консоли у свободного края h₁=300 мм.

Требуемая высота консоли у грани колонны:

h₀≥Q/(2.5*R_bt*b_col)=390.53/(2.5*1.08*0.4)=361.6 мм.

 

Принимаем h₀=h-a_s=600-50=550 мм.

Изгибающий момент в опорном сечении консоли:

 

M=1.25*Q*(l-Q/(2*R_b*b_p))=1.25*390.53*(300-390.53/(2*15.3*0.3))=125.68 кН*м.

 

Требуемая площадь сечения арматуры класса A400:

 

A_s=M/(R_s*(h₀-a_sc))=125.68/(365*(550-50))=688.7 мм².

 

Принимаем 3Æ18 A400; (A_s=763.4 мм²).

Вычисляем параметры консоли:

 

tgθ=(h₀-a_sc)/(a+0.5*l_sup)=(550-50)/(257.5+0.5*85.08)=1.667

 

θ=59.04˚

sinθ=0.857

cosθ=0.514

Ширина наклонной полосы:

 

l_b=l_sup*sinθ+2*5*cosθ=85.08*0.857+2*5*0.514=78.1 мм.

 

h=600<2,5*257.5=2,5*27=644, консоль армируется только наклонными хомутами по всей высоте.

Суммарная площадь наклонных хомутов (отгибов):

 

A_inc=[Q/(0.8*R_b*b_сol*l_b*sinθ)-1]*b_сol*S_inc/10*α=

=[390.53/(0.8*15.3*0.4*78.1*0.857)-1]*0.4*150/10*6.897=166.2 мм²,

где S_inc=150 мм – шаг отгибов:

S_inc£h/4=600/4=150 мм;

S_inc£150 мм.

α=6.897.

A_inc=0,002*b_сol*h₀=0,002*400*550=440 мм².

Требуемая площадь сечения одного хомута

 

A_inc1=A_inc/2*n=440/2*3=73 мм²

 

где n=3 – число пар наклонных хомутов.

По сортаменту подбираем отгибы Æ10 A400 (A_inc1=78.5 мм²).

Горизонтальные хомуты принимаем по конструктивным требованиям: Æ8 A400 с шагом S=150 мм.

 

Рис. 5.2. Армирование консоли колонны.

123456

Поделиться:

Воспользуйтесь поиском по сайту: