Анализ динамики производства молока

 

Рядом динамики называют ряд статистических показателей, характеризующих изменение явления во времени. Целью данного приёма является определение колеблемости явления во времени, выявление основной тенденции (тренда).

В качестве показателя, подлежащего анализу подлежит группировочный признак – удой молока от 1 коровы.

Простейшими показателями анализа, которые используются при решении ряда задач, в первую очередь при измерении скорости изменения уровня ряда динамики, являются абсолютный рост, темпы роста и прироста, а также абсолютное значение одного процента прироста. Расчёт этих показателей основан на сравнении между собой уровней ряда динамики. Если каждый уровень сравнивается с предыдущим, то полученные при этом показатели называются цепными. Если все уровни сравниваются с одним и тем же уровнем, выступающим как постоянная база сравнения, то полученные при этом показатели называются базисными.

Рассчитаем по первым десяти периодам следующие показатели рядов динамики: абсолютные приросты, коэффициенты роста, темпы роста и прироста. Для расчета этих показателей воспользуемся цепным и базисным способом. На основании полученных данных вычислим средние показатели динамики.

Абсолютные приросты рассчитываются:

а) цепным способом (А_ц):

А_ц1 = у₁-у₀, А_ц2=у₂-у₁ и т.д.

б) базисным способом (А_б)

А_б1 = у₁-у₀, А_б2 = у₂-у₀ и т.д.

Коэффициенты роста рассчитываются:

а) цепным способом (К_р^ц):

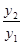К₁^ц= , К₂^ц=  и т.д.

б) базисным способом (К_р^б)

К₁^б= , К₂^б= 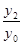 и т.д.

Темпы роста рассчитываются:

а) цепным способом (Т_р^ц)

Т_р^ц₁ = К_р^ц₁ * 100, Т_р^ц₂ = К_р^ц₂ * 100

б) базисным способом (Т_р^б)

Т_р^б₁ = К_р^б₁ * 100, Т_р^б₂ = К_р^б₂ * 100

Темпы прироста рссчитываются:

а) цепным способом (Т_пр^ц) = Т_р^ц - 100

б) базисным способом (Т_пр^б) = Т_р^б-100

Значение 1% прироста (З_пр) находится как сотая часть предыдущего уровня:

Рассчитанные показатели ряда динамики, оформив их в таблицу 10.

 

Таблица 10

Показатели динамики удоя молока от 1 коровы

Наименование показателей	Условное обозначение		Периоды									Средние значения
		0	1	2	3	4	5	6	7	8	9
		22,00	23,23	21,88	28,10	23,17	26,05	21,13	22,78	23,35	22,83	23,61
Абсолютный прирост, ц	Аб		1,23	-0,12	6,10	1,17	4,05	-0,87	0,78	1,35	0,83
	Ац		1,23	-1,35	6,22	-4,93	2,89	-4,93	1,65	0,58	-0,52	0,09
Коэффициент роста	Крб		1,06	0,99	1,28	1,05	1,18	0,96	1,04	1,06	1,04
	Крц		1,06	0,94	1,28	0,82	1,12	0,81	1,08	1,03	0,98	1,004
Темпы роста, %	Трб		105,58	99,46	127,72	105,30	118,43	96,03	103,53	106,15	103,79
	Трц		105,58	94,20	128,41	82,45	112,46	81,09	107,80	102,53	97,77	100,41
Темпы прироста, %	Тпрб		5,58	-0,54	27,72	5,30	18,43	-3,97	3,53	6,15	3,79
	Тпрц		5,58	-5,80	28,41	-17,55	12,46	-18,91	7,80	2,53	-2,23	0,41
Абсолютное значение 1% прироста	Зпр		0,22	0,23	0,22	0,28	0,23	0,26	0,21	0,23	0,23	0,22

 

Средний надой за 10 периодов составляет 23,61 ц. В среднем за 10 периодов наблюдается постоянное прирост удоя молока на 0,09 ц. Его уровень составлял в среднем 100,4 % от предыдущего. То есть за каждый период удой увеличивался на 0,4 %. Значение 1% прироста показывает, что в 1% изучаемого уровня содержится 0,22 ц. удоя молока.

Произведём выравнивание динамического ряда с целью выявления основной тенденции (тренда), используя выравнивание по средней скользящей (трёхлетней). (Таблица 11.)

 

Таблица 11

Исходные данные и результаты скользящей средней

производительности коров

№№ предприятий	Продуктивность коров, ц (Y1)	Сумма по скользящим 3-ём предприятиям	Средние скользящие
8	22,0	х	х
9	23,2	67,1	22,4
10	21,9	73,2	24,4
11	28,1	73,1	24,4
12	23,2	77,3	25,8
13	26,1	70,3	23,4
14	21,1	70,0	23,3
15	22,8	67,3	22,4
16	23,4	69,0	23,0
17	22,8	65,2	21,7
18	19,0	63,7	21,2
19	21,9	62,8	20,9
20	21,9	66,0	22,0
21	22,2	66,5	22,2
22	22,4	65,7	21,9
23	21,1	62,6	20,9
24	19,2	58,9	19,6
25	18,6	60,2	20,1
26	22,5	62,1	20,7
27	21,0	66,3	22,1
28	22,9	63,4	21,1
29	19,5	66,1	22,0
30	23,7	67,8	22,6
31	24,6	70,2	23,4
32	22,0	73,4	24,5
33	26,9	70,3	23,4
34	21,4	76,4	25,5
35	28,1	71,4	23,8
36	21,9	72,8	24,3
37	22,8	х	х

 

Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определённого числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго, далее начиная с третьего и т. д. Таким образом, при расчётах среднего уровня как бы скользят по временному ряду от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Каждое звено скользящей средней – это средний уровень за соответствующий период.

Из данных таблицы видно, что в первые 4 года наблюдается рост, затем до 16 года скачкообразное падение производительности, а после этого до 26 года вновь скачкообразный, но рост.

Применим аналитическое выравнивание. Исходя из предыдущих выводов, логично предположить, что для проявления тенденции можно использовать уравнение прямой. Но использование параболы второго порядка также возможно. Проверим оба варианта. Общий вид уравнений:

y = a₀ + a₁*t — уравнение прямой

y = a₀ + a₁*t + a_2*t².— уравнение параболы второго порядка

Осуществим выравнивание по уравнению прямой и по параболе второго порядка, сопоставим результаты и, найдя остаточные средние квадратическое отклонения, узнаем, какое из этих уравнений полнее отражает характер изменения удоя молока от 1 коровы.

Определим параметры уравнения прямой способом наименьших квадратов:

∑y_i = na₀ + a₁∑t_i;

∑y_i t = a₀∑t_i +a₁∑t²_i.

Для этого построим вспомогательную таблицу 12. Для упрощения расчётов воспользуемся способом отсчёта от условного начала. Система уравнений упрощается, поскольку ∑t=0.

Столбцы ỹ_t (y-ỹ_t)² рассчитывались после нахождения параметров уравнения прямой.

 

Таблица 12

Исходные данные и результаты выравнивания ряда динамики

производительности коров по прямой

№№ предприятий	Продуктивность коров, ц yt	Обоначение периода t	t2	y*t	ỹt	(y-ỹt)2
8	22,0	-29	841	-638,00	22,6	0,33
9	23,2	-27	729	-627,14	22,6	0,42
10	21,9	-25	625	-547,01	22,6	0,49
11	28,1	-23	529	-646,24	22,6	30,45
12	23,2	-21	441	-486,50	22,6	0,34
13	26,1	-19	361	-495,03	22,6	12,05
14	21,1	-17	289	-359,17	22,6	2,12
15	22,8	-15	225	-341,64	22,6	0,04
16	23,4	-13	169	-303,60	22,6	0,59
17	22,8	-11	121	-251,17	22,6	0,06
18	19,0	-9	81	-171,00	22,6	12,89
19	21,9	-7	49	-153,07	22,6	0,53
20	21,9	-5	25	-109,63	22,6	0,45
21	22,2	-3	9	-66,74	22,6	0,12
22	22,4	-1	1	-22,35	22,6	0,06
23	21,1	1	1	21,09	22,6	2,27
24	19,2	3	9	57,48	22,6	11,84
25	18,6	5	25	93,15	22,6	15,79
26	22,5	7	49	157,15	22,6	0,02
27	21,0	9	81	189,00	22,6	2,58
28	22,9	11	121	251,54	22,6	0,07
29	19,5	13	169	253,92	22,6	9,47
30	23,7	15	225	355,19	22,6	1,14
31	24,6	17	289	417,50	22,6	3,79
32	22,0	19	361	417,23	22,6	0,43
33	26,9	21	441	564,18	22,6	18,06
34	21,4	23	529	493,04	22,6	1,39
35	28,1	25	625	703,25	22,6	30,37
36	21,9	27	729	590,06	22,6	0,59
37	22,8	29	841	661,97	22,6	0,04
Итого	677,9	0	8990	7,46	677,9461	158,79

 

∑y_i = na₀ + a₁∑t_i;

∑y_i t = a₀∑t_i +a₁∑t²_i.

677,9=30* a₀+ a₁*0

7,46= a₀*0+ a₁*8990

а₁ = 7,46/8990 = 0,00083

а₀ = 677,9/30 = 22,6

Уравнение прямой имеет вид: у=22,6 + 0,00083*t

Коэффициент а₁ характеризует средний рост удоя молока от 1 коровы.

Используем для выравнивания уравнение параболы второго порядка y_i = a₀ + a₁t + a₂t². Для нахождения параметров а₀, а₁, а₂ применим систему нормальных уравнений:

∑y_i = na₀ + a₁∑t +a₂∑t²

∑y_it = a₀∑t + a₁∑t² +a₂∑t³

∑y_it² =a₀∑t² + a₁∑t³+ a₂∑t⁴

Подготовим данные для выравнивания ряда динамики произ-водительности коров по уравнению параболы второго порядка (таблица 13).

 

Таблица 13

Исходные данные и результаты выравнивания ряда динамики

производительности коров по уравнению параболы второго порядка

№№ предприятий	Продуктивность коров, ц yt	Обозначение периода t	t^2	y*t	y*t^2	t^4	ỹt	(y-ỹt)^2
8	22,0	-29	841	-638,0	18502,0	707281	24,5	6,1
9	23,2	-27	729	-627,1	16932,7	531441	24,1	0,7
10	21,9	-25	625	-547,0	13675,2	390625	23,7	3,4
11	28,1	-23	529	-646,2	14863,5	279841	23,4	22,2
12	23,2	-21	441	-486,5	10216,5	194481	23,1	0,0
13	26,1	-19	361	-495,0	9405,5	130321	22,8	10,6
14	21,1	-17	289	-359,2	6105,9	83521	22,5	2,0
15	22,8	-15	225	-341,6	5124,7	50625	22,3	0,2
16	23,4	-13	169	-303,6	3946,8	28561	22,1	1,5
17	22,8	-11	121	-251,2	2762,8	14641	22,0	0,8
18	19,0	-9	81	-171,0	1539,0	6561	21,8	8,0
19	21,9	-7	49	-153,1	1071,5	2401	21,7	0,0
20	21,9	-5	25	-109,6	548,1	625	21,6	0,1
21	22,2	-3	9	-66,7	200,2	81	21,6	0,4
22	22,4	-1	1	-22,4	22,4	1	21,5	0,6
23	21,1	1	1	21,1	21,1	1	21,6	0,2
24	19,2	3	9	57,5	172,4	81	21,6	5,9
25	18,6	5	25	93,1	465,7	625	21,6	9,1
26	22,5	7	49	157,2	1100,1	2401	21,7	0,5
27	21,0	9	81	189,0	1701,0	6561	21,8	0,7
28	22,9	11	121	251,5	2766,9	14641	22,0	0,8
29	19,5	13	169	253,9	3301,0	28561	22,2	6,9
30	23,7	15	225	355,2	5327,8	50625	22,3	1,8
31	24,6	17	289	417,5	7097,5	83521	22,6	3,9
32	22,0	19	361	417,2	7927,4	130321	22,8	0,8
33	26,9	21	441	564,2	11847,8	194481	23,1	14,1
34	21,4	23	529	493,0	11339,8	279841	23,4	3,9
35	28,1	25	625	703,3	17581,3	390625	23,8	19,1
36	21,9	27	729	590,1	15931,6	531441	24,1	5,2
37	22,8	29	841	662,0	19197,0	707281	24,5	2,9
Итого	677,9	0	8990	7,5	210695,3	4842014	677,9	132,3

 

677,9 = 30*a₀ + 0*a₁ +8990*a₂

7,5 = 0*a₀ + 8990*a₁ +0*a₂

210695,3 =8990*a₀ + 0*a₁+ 4842014*a₂

 

Решив систему уравнений получаем параметры:

a₀ = 21,55

a₁ = 0,00083

a₂ = 0,0035

Уравнение параболы имеет вид: у=21,55 + 0,00083*t+0.0035*t²

Параметр уравнения а₁ = 0,00083 ц показывает средний рост удоя молока от одной коровы за год; а₂ = 0,0035 ц – степень нарастания роста, то есть ускорение роста.

А теперь определим, какое из этих уравнений наиболее точно отражает характер изменения удоя во времени.

σ _пр = = = 2,3

σ _пар = 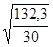=2,1

Остаточное среднее квадратическое отклонение, полученное при выравнивании по параболе меньше, чем среднее квадратическое отклонение при выравнивании по прямой. Следовательно, парабола более точно воспроизводит характер изменения удоя молока от 1 коровы за анализируемый период. Это хорошо иллюстрирует график.

 

 

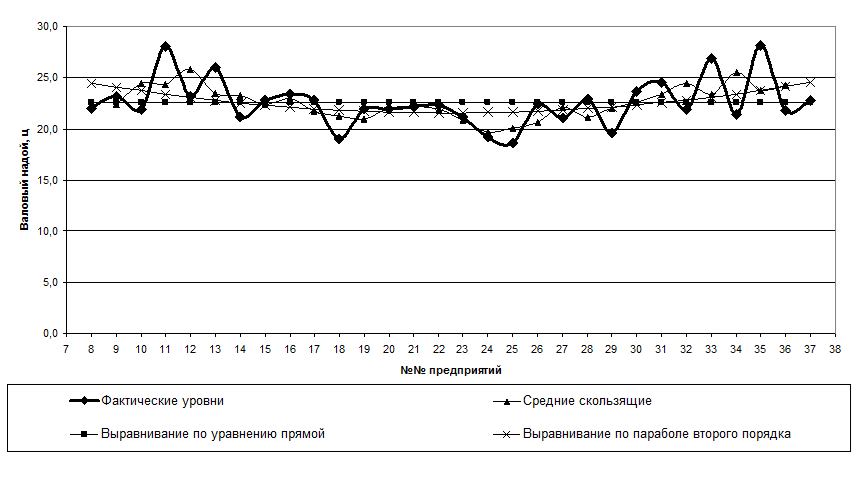
Рис.4. Выравнивание ряда динамики

 

Фактические значения удоя молока от одной коровы имеют значительную колеблемость за указанный период (от 18,63 ц до 28,13 ц). На основании тренда можно сказать, что на данном временном интервале наблюдается ускорение тенденции к росту уровня.

12345

Поделиться:

Воспользуйтесь поиском по сайту: