 |
Алгоритмы поиска путей в графе.
|
|
|
|
ЗАДАЧИ ДЛЯ ПРОГРАММИРОВАНИЯ ПО ТЕМАМ
″ТЕОРИЯ ГРАФОВ″, ″РЕКУРСИВНЫЕ ФУНКЦИИ″, ″МАШИНЫ ТЬЮРИНГА″
направление ″БИЗНЕС-ИНФОРМАТИКА″,
специальность ″МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ″
Вопросы:
1. Обходы графа. Вычисление числа компонент связности графа.
2. Алгоритмы поиска путей в графе.
3. Алгоритмы нахождения минимального остова в графе.
4. Хроматическое число графа. Алгоритм правильной раскраски вершин графа методом перебора с возвратами.
5. Транспортные сети. Теорема Форда-Фалкерсона о максимальном потоке в транспортной сети.
6а. Варианты задач для групп по направлению ″Бизнес-информатика″. Тема ″Транспортные сети″
6б. Варианты задач для групп по специальности ″Математические методы в экономике″. Тема ″Транспортные сети″
7. Задачи по теме ″Рекурсивные функции″.
8. Задачи по теме ″Машины Тьюринга″.
ОБХОДЫ ГРАФА. ВЫЧИСЛЕНИЕ ЧИСЛА КОМПОНЕНТ СВЯЗНОСТИ ГРАФА.
Определение. Обход графа – это прохождение его вершин в некотором систематическом порядке.
Решение многих задач теории графов связано с организацией систематического обхода всех вершин графа. Существуют два наиболее часто используемых метода обхода графов: поиск в глубину и поиск в ширину.
Поиск в глубину ПВГ в графе 
с множеством вершин 
и множеством рёбер 
начинается с произвольной вершины 
. Для помечивания пройденных вершин используется массив 
, где 
− метка вершины 
, причём 
, если − ещё не посещенная вершина, а 
− если уже посещенная. Для организации обхода используется стек 
, в вершину которого помещается текущая пройденная вершина.
Алгоритм ПВГ (
, 
) ≡ {
S ← ∅; опустошаем стек
|
|
|
my ← 1; помечаем вершину v
S ⟸ v; помещаем вершину v в стек
while S ≠ ∅ do продолжаем обход, пока стек не пуст
a ⟸ S; извлекаем очередную вершину из стека
if существует ребро (a,b) ∈ E с непомеченной вершиной b
then {
S ⟸ a; возвращаем вершину a в стек
mb ← 1; помечаем вершину b
S ⟸ b помещаем вершину b в стек
od
}.
Т.о., при поиске (обходе) в глубину после очередной посещённой вершины посещается любая смежная с ней вершина 
. Если все вершины, смежные с , уже посещались, то происходит возврат к вершине 
, предыдущей по отношению к 
Поиск (обход) в ширину ПВШ отличается от ПВГ тем, что вначале посещаются вершины, смежные с исходной, затем смежные с посещёнными и т.д. Если считать, что смежные вершины находятся на расстоянии 1 друг от друга, то вначале посещаются вершины, находящиеся на расстоянии 1 от исходной, затем вершины, находящиеся на расстоянии 2, и т.д. Для реализации алгоритма требуется очередь 
.
Алгоритм ПВШ (, ) ≡ {
Q ← ∅; опустошаем очередь
mv ← 1; помечаем вершину v
Q ⟸ v; помещаем вершину v в очередь
while Q ≠ ∅ do продолжаем обход, пока очередь не пуста
a ⟸ Q; извлекаем очередную вершину из очереди
while существует ребро (a,b) ∈ E с непомеченной вершиной b
do
mb ← 1; помечаем вершину b
Q ⟸ b помещаем вершину b в очередь
od
od}.
Определение. Максимальный связный подграф графа называется компонентой связности графа 
. Несвязный граф состоит из нескольких компонент связности.
Пример использования обхода графа.
Алгоритм вычисления k − числа компонент связности графа:
k ← 0;
for v ← 1 to n do mv ← 0;
for v ← 1 to n do {
if mv = 0 then {s ← s + 1; ПВГ (, ) или ПВШ (, ) }.
АЛГОРИТМЫ ПОИСКА ПУТЕЙ В ГРАФЕ.
Постановка задачи. Дан простой ориентированный граф с множеством вершин и множеством рёбер 
(без петель и кратных дуг). На множестве дуг задана неотрицательная вещественная функция 
(длины дуг). Длина пути из вершины в вершину 
определяется как сумма длин дуг, составляющих путь.
|
|
|
Задача 1. Одна из вершин выделена как источник. Требуется найти кратчайшие пути из источника ко всем остальным вершинам.
Задача 2. Найти кратчайшие пути между всеми парами вершин.
Для решения задачи 1 рассмотрим ″жадный″ алгоритм Дейкстры:
Алгоритм строит (использует) множество вершин, для которых кратчайшие пути из источника уже найдены. На каждом шаге к множеству добавляется та из оставшихся вершин 
которая ближе к источнику по сравнению с другими оствшимися вершинами. Так как длины дуг неотрицательны, то можно быть уверенны в том, что кратчайший путь проходит от источника к конкретной вершине через вершины множества . На каждом шаге алгоритма используется массив 
, в который записываются длины кратчайших путей для каждой вершины. Причём если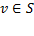 
, то значение 
становится окончательным.
Алгоритм Дейкстры
Пусть dist – двумерный массив, причём dist [v,w] равно длине дуги (v,w) из вершины v в вершину w. Если такой дуги не существует, то полагаем dist [v,w]= ∞.
S ← {1}; вершина 
взята как источник
L[1] ← 0;
for v ← 2 to n do
L[v] ← dist [1,v]; pred[v] ← v
od;
for i ← 1 to n − 1 do
найдём вершину w ∈ V \ S, для которой значение L[w]минимально;
S ← S ∪ {w};
for ∀v ∈ V \ S do
m ← L[w] + dist [w,v];
if L[v] > m then {L[w]← m; pred[v] ← w
od
od.
Результат: L[v]− длина кратчайшего пути из вершины 1 в вершину v. При этом v, pred[v], pred[pred[v]],..., 1 есть вершины, составляющие кратчайший путь из вершины 1 в вершину v.
Обоснование алгоритма Дейкстры (кратко )
Допустим, что для полученного пути из источника в имеется более короткий путь в , который проходит до вершины 
через вершины множества и выходит из него, затем путь, возможно, несколько раз заходит в и выходит из него, пока не достигнет вершины . В этом случае вместо была бы выбрана вершина 
. Противоречие.
Другая возможность кратчайшего пути не реализуема, поскольку путь из в 
через вершины множества короче, чем через вершину 
по построению.
Рассмотренный алгоритм имеет временн 
ю сложность O (
). Для рещения второй задачи существует алгоритм (Флойда, основанный на процедуре Уорщолла для вычисления транзитивного замыкания) со сложность O (
), причем допускаются даже отрицательные веса дуг графа.
|
|
|
|
|
|
