 |
Алгоритм Форда-Фалкерсона.
|
|
|
|
Вход: транспортная сеть  , заданная матрицей (
, заданная матрицей ( ), где
), где  =
=  (
( ,
,  ),
),  ,
, 
 , пропускных способностей, или каким-нибудь другим способом.
, пропускных способностей, или каким-нибудь другим способом.
(Начинаем с нулевого потока.)
for  е ∈ E do f(e) := 0;
е ∈ E do f(e) := 0;
(Фаза 1.)
Удаляем все метки вершин;
Помечаем источник;
while вершина t не помечена и существует непомеченная вершина v do
помечаем вершину v;
od;
if сток не помечен then конец: максимальный поток построен;
(Фаза 2.)
v:= t; u:= dv;
while v ≠ s do
if bv = ″+″ then f(u,v):= f(u,v)+ ∆t
else f(u,v):= f(u,v)− ∆t;
v:= u
od;
Возврат на фазу1.
Выход: максимальный потокf.
6а. ВАРИАНТЫ ЗАДАЧ ДЛЯ ГРУПП ПО НАПРАВЛЕНИЮ ″БИЗНЕС-ИНФОРМАТИКА″
ТЕМА ″ТРАНСПОРТНЫЕ СЕТИ″
Транспортная сеть задана списком дуг  , где
, где  – начало дуги,
– начало дуги,  – конец дуги, а
– конец дуги, а  – пропускная способность дуги.
– пропускная способность дуги.
1. Построить все  -разрезы сети;
-разрезы сети;
2. Используя помечающий алгоритм, построить максимальный поток  сети и вычислить его значение.
сети и вычислить его значение.
3.
| ГРУППА БИЗНЕС-ИНФОРМАТИКА 2 КУРС 2011∕ 2012 УЧ. ГОД | ||
| ВАРИАНТ | ФИО | Оценка |
| ЭКОНОМФАК | ||
| Валиева Эльвира | ||
| Гильмутдинова Фарида | ||
| Гилязова Эльвира | ||
| Залялиева Динара | ||
| Исмоилова Фируза | ||
| Каримуллин Алмаз | ||
| Коган Илья | ||
| Крылов Сергей | ||
| Лабутин Евгений | ||
| Мошкова Наталья | ||
| Мухаметшина Лиля | ||
| Сибгатуллина Дина | ||
| Скарлыгина Диана | ||
| Хайруллина Эвилина | ||
| Хайсарова Резеда | ||
| Шамсутдинова Айшна | ||
| ВМК (ВМиИТ) | ||
| Калита Екатерина | ||
| Латыпова Наиля | ||
| Мухамедова Алина | ||
| Трушина Екатерина | ||
| Слухов Андрей | ||
| Шакиров Ренат |
| ВАРИАНТ 1 | ВАРИАНТ 2 | ВАРИАНТ 3 | ВАРИАНТ 4 | ВАРИАНТ 5 | ВАРИАНТ 6 |

| 
| 
| 
| 
| 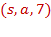
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 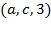
|
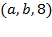
| 
| 
| 
| 
| 
|
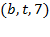
| 
| 
| 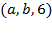
| 
| 
|

| 
| 
| 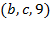
| 
| 
|

| 
| 
| 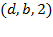
| 
| 
|
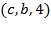
| 
| 
| 
| 
| 
|
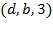
| 
| 
| 
| 
| 
|
| ВАРИАНТ 7 | ВАРИАНТ 8 | ВАРИАНТ 9 | ВАРИАНТ 10 | ВАРИАНТ 11 | ВАРИАНТ 12 |
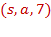
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
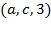
| 
| 
| 
| 
| 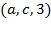
|
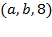
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 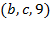
| 
| 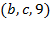
| 
| 
|

| 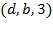
| 
| 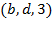
| 
| 
|

| 
| 
| 
| 
| 
|
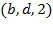
| 
| 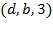
| 
| 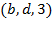
| 
|
| ВАРИАНТ 13 | ВАРИАНТ 14 | ВАРИАНТ 15 | ВАРИАНТ 16 | ВАРИАНТ 17 | ВАРИАНТ 18 |

| 
| 
| 
| 
| 
|
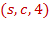
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 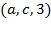
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
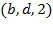
| 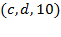
| 
| 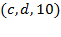
| 
| 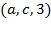
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
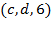
| 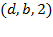
| 
| 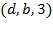
| 
| 
|
| ВАРИАНТ 19 | ВАРИАНТ 20 | ВАРИАНТ 21 | ВАРИАНТ 22 | ВАРИАНТ 23 | ВАРИАНТ 24 |
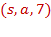
| 
| 
| 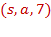
| 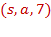
| 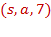
|

| 
| 
| 
| 
| 
|

| 
| 
| 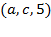
| 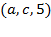
| 
|

| 
| 
| 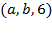
| 
| 
|
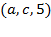
| 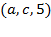
| 
| 
| 
| 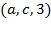
|
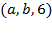
| 
| 
| 
| 
| 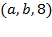
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 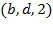
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 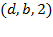
| 
| 
| 
| 
|
6б. ВАРИАНТЫ ЗАДАЧ ДЛЯ ГРУПП ПО СПЕЦИАЛЬНОСТИ ″МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ″
|
|
|
ТЕМА ″ТРАНСПОРТНЫЕ СЕТИ″
Транспортная сеть задана списком дуг  , где
, где  – начало дуги,
– начало дуги,  – конец дуги, а
– конец дуги, а  – пропускная способность дуги.
– пропускная способность дуги.
1. Построить все  -разрезы сети;
-разрезы сети;
2. Используя помечающий алгоритм, построить максимальный поток  сети и вычислить его значение.
сети и вычислить его значение.
| ГРУППА ЭКОНОМ. КИБЕРНЕТИКА 2 КУРС 2011∕ 2012 УЧ. ГОД | ||
| ВАРИАНТ | ФИО | Оценка |
| Ахметзянова Лилия | ||
| Билалова Лейла | ||
| Вафина Альфинур | ||
| Гараева Гульшат | ||
| Глебова Валерия | ||
| Зюмрва Елена | ||
| Крылов Сергей | ||
| Райхлина Екатерина | ||
| Савельева Маргарита | ||
| Салихова Айназ | ||
| Титоренко Роман | ||
| Тубольцева Ксения | ||
| Фейсханов Алмаз | ||
| Цуканова Ольга | ||
| Чудаева Алина | ||
| Шайдулова Софья | ||
| Яковлева Екатерина |
7.ЗАДАЧИ по теме ″РЕКУРСИВНЫЕ ФУНКЦИИ″.
1. Доказать, что следующие функции примитивно рекурсивны:
1)  (где
(где  − константа)
− константа) 
2) 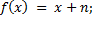
3) 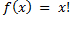 (где
(где  )
) 
4) 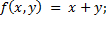
5) 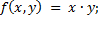
6)  (где
(где  )
) 
7) 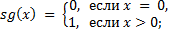
8) 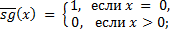
9) 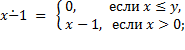
10) 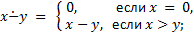
11)  ,
,  ;
;
12) |  ;
;
13 ) 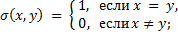
14) 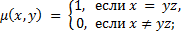
15)  − функции алгебры логики (отрицание, дизъюнкция, конъюнкция), где чётные числа трактуются как
− функции алгебры логики (отрицание, дизъюнкция, конъюнкция), где чётные числа трактуются как  , а нечётные
, а нечётные  как
как  , т.е.
, т.е.
|
|
|
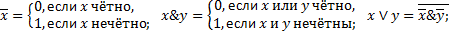
16) 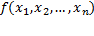 − произвольная функция алгебры логики;
− произвольная функция алгебры логики;
17)  где
где  примитивно рекурсивная функция,
примитивно рекурсивная функция,  ;
;
18)  где
где  примитивно рекурсивная функция,
примитивно рекурсивная функция,  ;
;
19)  (здесь
(здесь  );
);
20) rest ( ,
,  )
)  (здесь rest(
(здесь rest( ,
,  )
)  );
);
21)  (при фиксированном
(при фиксированном  );
);
22)  (при фиксированном
(при фиксированном  ,
,  );
);
23) ( ,
,  )
)  наибольший общий делитель чисел
наибольший общий делитель чисел  и
и  (здесь (
(здесь ( ,
,  ) = 0);
) = 0);
24) [  ,
,  ]
]  наименьшее общее кратное чисел
наименьшее общее кратное чисел  и
и  (здесь [
(здесь [  ,
,  = [
= [  ,
,  ]
]  0);
0);
25)  − число сочетаний из
− число сочетаний из  по
по  (здесь
(здесь  0 при
0 при  );
);
26) 
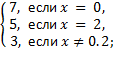
27) 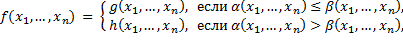
где  ,
,  ,
,  ,
,  примитивно рекурсивные функции от переменных
примитивно рекурсивные функции от переменных  .
.
2. Применяя операцию примитивной рекурсии к функциям 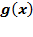 и
и  , определить функцию
, определить функцию 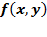 и записать её в аналитической форме:
и записать её в аналитической форме:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  ;
;
4)  ,
,  ;
;
5)  ,
,  ;
;
6)  ,
,  ;
;
7) 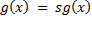 ,
,  ;
;
8)  ,
, 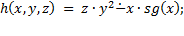
9) 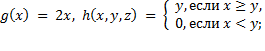
10) 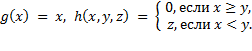
3. Вычислить соответствующую функцию, применяя операцию минимизации. Результаты представить в аналитической форме:
1)  [|
[|  −3| = 0];
−3| = 0];
2)  [|
[| 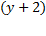 −
− 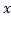 | = 0];
| = 0];
3)  [|
[|  −
− 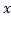 | = 0];
| = 0];
4)  [
[ 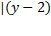 −
−  = 0];
= 0];
5)  [|
[|  −
− 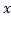 |= 0];
|= 0];
6)  [|
[| 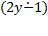 −
− 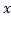 | = 0];
| = 0];
7)  [|
[|  −
− 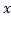 | = 0];
| = 0];
8)  [|
[|  −
− 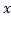 | = 0];
| = 0];
9)  [|
[| 
 −
− 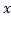 | = 0];
| = 0];
10)  [|
[|  −
−  | = 0];
| = 0];
11)  [|
[|  −
−  | = 0];
| = 0];
12)  [|
[|  −
−  | = 0];
| = 0];
13)  [|
[|  −
−  | = 0];
| = 0];
14)  [|
[|  −
−  | = 0].
| = 0].
4. Доказать, что следующие функции частично рекурсивны:
1) 
 нигде не определённая функция;
нигде не определённая функция;
2) 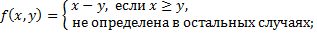
3) 
4) 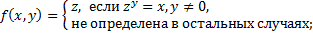
6)  функция, определённая только при
функция, определённая только при  ,
, 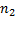 ,…,
,…,  .
.
5. Найти примитивно рекурсивную функцию, из которой однократным применением операции минимизации можно получить частично рекурсивную функцию  :
:
1)  ;
;
2)  ;
;
3) 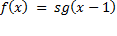 ;
;
4) 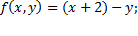
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  .
.
8. ЗАДАЧИ ПО ТЕМЕ ″МАШИНЫ ТЬЮРИНГА″
1. (Гаврилов Г. П., Сапоженко А.А. Задачник. С. 220, № 1.1.) Установить, применима ли машинаТьюринга  , заданная программой
, заданная программой  , к слову
, к слову  . Если применима, найти рельтат применения. Предполагается, что
. Если применима, найти рельтат применения. Предполагается, что 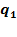 − начальное,
− начальное,  − заключительное состояния машины, а
− заключительное состояния машины, а  начальная конфигурация.
начальная конфигурация.

| 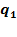
| 
| 
| 
| 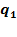
| 
| 
| 
| 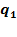
| 
| 
| ||
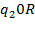
| 
| 
| 
| 
| 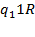
| 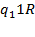
| 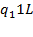
| ||||||
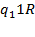
| 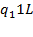
| 
| 
| 
| 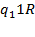
| 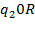
| 
| ||||||
a)  б)
б)  в)
в) 
| a)  б)
б)  в)
в) 
| a)  б)
б)  в)
в) 
| |||||||||||
2. (Гаврилов Г. П., Сапоженко А.А. Задачник. С. 220-221, идея из № 1.2.) Построить машину  в алфавите
в алфавите 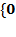 ,
,  , которая:
, которая:
a) применима к любой непустой ленте (т.е. останавливается лишь в том случае, если хотя бы в одной из ячеек записан символ  ; зона действия − бесконечная слева и справа от начальной обозреваемой ячейки);
; зона действия − бесконечная слева и справа от начальной обозреваемой ячейки);
б) применима к словам вида 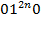 и не применима к словам вида
и не применима к словам вида  ;
;
|
|
|
в) применима только к словам вида  (
( );
);
г) применима к словам вида  (
(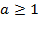 ) и не применима к словам вида
) и не применима к словам вида  , если
, если  .
.
3. (Гаврилов Г. П., Сапоженко А.А. Задачник. С. 221, № 1.3.) По заданной машине Тьюринга  и начальной конфигурации
и начальной конфигурации  найти заключительную конфигурацию:
найти заключительную конфигурацию:

| 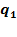
| 
| 
| 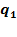
| 
| 
| |

| 
| ||||||
|
|
|


