 |
Транспортные сети. Теорема форда-фалкерсона о максимальном потоке в транспортной сети
|
|
|
|
Определение.Транспортная сеть − это связный ориентированный граф 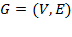 без петель, удовлетворяющий следующим условиям:
без петель, удовлетворяющий следующим условиям:
1. Существует только одна вершина с нулевой степенью захода; эта вершина называется источником и обозначается через  .
.
2. Существует только одна вершина с нулевой степенью исхода; эта вершина называется стоком и обозначается через  .
.
3. Каждой дуге  в сети
в сети  сопоставляется неотрицательное вещественное число, называемое пропускной способностью дуги
сопоставляется неотрицательное вещественное число, называемое пропускной способностью дуги  ; оно обозначается через
; оно обозначается через 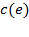 или
или  . (Если не существует дуги, ориентированной из
. (Если не существует дуги, ориентированной из  в
в  , то полагаем, что
, то полагаем, что  .)
.)
Моделью транспортной сети может служить водопроводная система, в которой сечения труб определяют пропускные способности соответствующих труб, т.е. количество жидкости. которое может пропустить труба за единицу времени.
Потоком 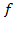 в транспортной сети
в транспортной сети  является функция, сопоставляющая каждой дуге
является функция, сопоставляющая каждой дуге  неотрицательное вещественное число
неотрицательное вещественное число  так, что выполняются следующие условия:
так, что выполняются следующие условия:
1. 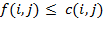 для любой дуги
для любой дуги  ;
;
2.  для любого
для любого  .
.
(Требование 2 − это условие сохранения баланса. Образно говоря, ″сколько втекает в вершину, столько и вытекает из неё″.)
Величина потока  обозначается через
обозначается через  и определяется выражением
и определяется выражением
 .
.
Говорят, что поток  максимален, если не существует потока
максимален, если не существует потока  такого, что
такого, что  >
>  .
.
Постановка задачи. Найти максимальный поток в заданной транспортной сети.
Пусть  ,
,  . Разрез
. Разрез  ,
,  определяется как множество дуг
определяется как множество дуг  , у которых начало и конец лежат в разных подмножествах
, у которых начало и конец лежат в разных подмножествах  и
и  . Разрез состоит из прямых дуг, ориентированных из
. Разрез состоит из прямых дуг, ориентированных из  в
в  , и обратных дуг, ориентированных из
, и обратных дуг, ориентированных из  в
в  . Если
. Если  ,
,  , то соответствующий разрез называется (
, то соответствующий разрез называется ( -
-  ) - разрезом. См. рис. 1.
) - разрезом. См. рис. 1.
Далее рассматриваются только  -
-  - разрезы.
- разрезы.
Пропускная способность  ,
,  разреза
разреза  ,
,  определяется как сумма пропускных способностей прямых дуг разреза. Разрез, пропускная способность которого не больше, чем у любого другого разреза, называется минимальным. (В транспортной сети может быть несколько минимальных разрезов, конечно, с одинаковыми пропускными способностями.)
определяется как сумма пропускных способностей прямых дуг разреза. Разрез, пропускная способность которого не больше, чем у любого другого разреза, называется минимальным. (В транспортной сети может быть несколько минимальных разрезов, конечно, с одинаковыми пропускными способностями.)
|
|
|
Поток из  в
в  определяется как
определяется как
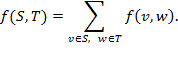
Аналогично определяется поток из  в
в  :
:
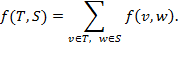
1. Лемма. Для любого  -
-  - разреза <
- разреза <  ,
,  > имеет место равенство
> имеет место равенство
 .
.
Доказательство. Для фиксированного  имеем
имеем
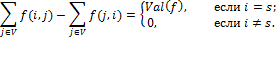
Суммируя по всем  , получаем
, получаем
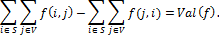
С другой стороны,
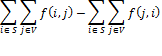
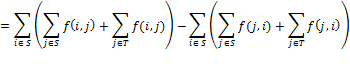
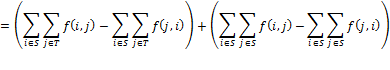
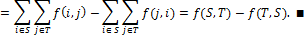
2. Следствие. Для любого потока  и любого
и любого  -
-  - разреза <
- разреза <  ,
,  >
>
 (
( ,
,  ).
).
Доказательство.  . ∎
. ∎
Для потока  и разреза <
и разреза <  ,
,  > прямую дугу
> прямую дугу  , где
, где  ,
, 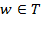 , будем называть
, будем называть  - насыщенной (соответственно,
- насыщенной (соответственно,  - не
- не  ), если
), если  (соответственно, если
(соответственно, если 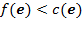 ). Обратную дугу
). Обратную дугу  , где
, где  ,
,  , будем называть
, будем называть  - нулевой (соответственно,
- нулевой (соответственно,  - положительной), если
- положительной), если  (соответственно, если
(соответственно, если  ).
).
3. Лемма. Если величина потока  равна пропускной способности некоторого разреза
равна пропускной способности некоторого разреза  ,
,  , то
, то  − максимальный поток, а
− максимальный поток, а 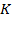 − минимальный разрез. Для данного разреза прямые дуги являются насыщенными, а обратные − нулевыми.
− минимальный разрез. Для данного разреза прямые дуги являются насыщенными, а обратные − нулевыми.
Доказательство. Пусть  − максимальный поток, а
− максимальный поток, а  − минимальный разрез. Так как
− минимальный разрез. Так как  и, по условию,
и, по условию,  , то
, то 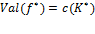 . ∎
. ∎
Рассмотрим в транспортной сети цепочку  рёбер
рёбер
 ,
,  ,
,  ,
,  ,
,  ,
,
соединяющую источник  и некоторую вершину
и некоторую вершину  . Заметим, что рёбра получаются из дуг путём снятия ориентации. Соответствующие дуги, составляющие цепочку, могут быть как прямыми, т.е. ориентированными из
. Заметим, что рёбра получаются из дуг путём снятия ориентации. Соответствующие дуги, составляющие цепочку, могут быть как прямыми, т.е. ориентированными из  в
в  , так и обратными, т.е. ориентированными из
, так и обратными, т.е. ориентированными из  в
в  .
.
Для ребра  полагаем
полагаем
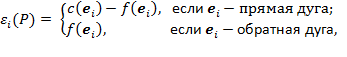
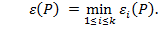
Цепочка  называется
называется  - ненасыщенной, если
- ненасыщенной, если  .
.  -ненасыщенная цепочка из
-ненасыщенная цепочка из  в
в  называется
называется  - дополняющей.
- дополняющей.
Наличие в сети  -дополняющей цепочки
-дополняющей цепочки  позволяет увеличить величину потока, вводя новый поток
позволяет увеличить величину потока, вводя новый поток 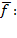

При этом
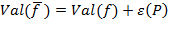 .
.
4. Теорема. Поток  в транспортной сети максимален тогда и только тогда, когда в сети отсутствуют
в транспортной сети максимален тогда и только тогда, когда в сети отсутствуют  -дополняющие цепочки.
-дополняющие цепочки.
|
|
|
Доказательство. Необходимость. Если поток максимален, то в сети заведомо нет  -дополняющих цепочек. В противном случае можно было бы построить новый поток
-дополняющих цепочек. В противном случае можно было бы построить новый поток  , величина которого больше, чем у потока
, величина которого больше, чем у потока  .
.
Достаточность. Предположим, что сеть с потоком  не содержит
не содержит  -дополняющих цепочек. Покажем, что в этом случае
-дополняющих цепочек. Покажем, что в этом случае  − максимальный поток.
− максимальный поток.
Разобьём множество  вершин сети на два непересекающихся подмножества
вершин сети на два непересекающихся подмножества  и
и  : в
: в  включим те вершины
включим те вершины  , до которых существуют
, до которых существуют  -ненасыщенные цепочки из источника
-ненасыщенные цепочки из источника  , а в
, а в  включим остальные вершины, т.е.
включим остальные вершины, т.е.  . Очевидно, что
. Очевидно, что  .
.
Пусть  − произвольная дуга разреза
− произвольная дуга разреза  ,
,  . Если
. Если  − прямая дуга, т.е.
− прямая дуга, т.е.  ,
, 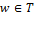 , то
, то  является
является  -насыщенной дугой, поскольку иначе существует
-насыщенной дугой, поскольку иначе существует  -ненасыщенная цепочка из
-ненасыщенная цепочка из  в
в  и
и  . Аналогично, если
. Аналогично, если  − обратная дуга, т.е.
− обратная дуга, т.е.  ,
,  , то
, то  является
является  -нулевой дугой
-нулевой дугой  . Таким образом,
. Таким образом,  для прямых дуг и
для прямых дуг и  для обратных дуг разреза <
для обратных дуг разреза <  ,
,  >. Тогда
>. Тогда  ,
,  ,
,  ,
,  ,
,  и
и  ,
,  ,
,  ,
,  . Из леммы 3 вытекает, что <
. Из леммы 3 вытекает, что <  ,
,  > − минимальный разрез, а
> − минимальный разрез, а  − максимальный поток .∎
− максимальный поток .∎
5. Следствие (теорема Форда-Фалкерсона). Величина максимального потока в транспортной сети равна пропускной способности минимального разреза.
|
|
|


