 |
Вероятность безотказной работы
|
|
|
|
Вероятность безотказной работы – вероятность того, что в пределах заданной наработки отказ не возникнет. Вероятностью события Pi называется отношение числа случаев, благоприятствующих к наступлению данного события mi ко всему числу случаев n, т.е.
Вероятность безотказной работы объекта за время t есть функция 
,
где T1 – время от начала работы объекта до его отказа; t - время, в течение которого определяется P(t).
В статистической форме 
где N0 – число объектов в начале испытаний; n(t) – число отказавших за время t.
Соответственно, вероятность отказа за время t 
Так как безотказная работа и отказ – события противоположные, т.е. два совместных события, образующих группу событий, то 
Откуда
Вероятность отказа в единицу времени - плотность вероятности отказов:
в вероятностной форме 
; в статистической 
,
где n(t) – число отказавших объектов в интервале от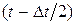 
до 
;
- выбранный интервал времени.
Вероятность отказов в единицу времени f(t) наиболее полно характеризует такую величину, как время возникновения отказа. Остальные величины могут быть получены, если известна f(t), которая является функцией плотности распределения.
Типичная кривая изменения плотности вероятности отказов f(t) для большинства горных машин в течение всего срока эксплуатации имеет вид
 |
Участок (0– t 1) – приработка элементов в начале эксплуатации. Большое число отказов объясняется внутренними скрытыми дефектами в элементах, вызванными нарушением технологии их изготовления.
Период (t 1- t 2) – нормальная работа объекта. Отказы обусловлены в основном неблагоприятным стечением обстоятельств, сочетанием пиковых нагрузок, низкими механическими свойствами материала, неточностью сборки, вибрацией.
|
|
|
Момент времени (t 2- t 3) характеризуется резким ростом вероятности отказов в единицу времени f(t) вследствие износа и старения элементов.
После t3 уменьшение f(t) является следствием незначительного количества оставшихся в эксплуатации объектов, которые характеризуются повышенной надежностью.
В зависимости от вида изделий и стадий эксплуатации объектов плотность вероятности отказов может соответствовать одному из следующих законов распределения случайных величин:
- Экспоненциальный 
, где 
;
- Нормальный 
- Закон распределения Вейбулла 
,
где 
, 
- параметры закона распределения; 
- математическое ожидание случайной величины; 
- среднеквадратическое отклонение.
Экспоненциальный закон характерен для периода нормальной эксплуатации машин, когда износовые отказы еще не проявляются. Нормальный закон характерен для износовых отказов электрических и механических элементов, когда время возникновения отказов зависит от большого числа однородных по своему влиянию случайных факторов (причем влияние каждого из этих факторов по сравнению с совокупностью всех остальных незначительно). Распределение Вейбулла может быть использовано для характеристики надежности горных машин в периоды приработки, а также износа и старения (в частности, при изучении надежности подшипников). Экспоненциальный является частным случаем закона Вейбулла при 
.
Таким образом, вышеуказанные законы распределения времени отказов могут характеризовать плотность вероятности отказов f(t) лишь на ограниченных участках времени работы объектов (систем).
Закон распределения отказов, как правило, определяется по экспериментальным данным. Однако часто делается обоснованное предположение о законе распределения отказов для конкретных систем на основе сравнительного анализа, а опытные данные служат средством проверки прогноза.
|
|
|
|
|
|
