 |
Золотое сечение - гармоническая пропорция
|
|
|
|
Ф. В. Ковалев
Золотое сечение
в живописи
Допущено
Министерством культуры УССР
в качестве учебного пособия
для художественных институтов
и училищ
КИЕВ
ГОЛОВНОЕ ИЗДАТЕЛЬСТВО
ИЗДАТЕЛЬСКОГО ОБЪЕДИНЕНИЯ
«ВЫЩА ШКОЛА»
ББК 85.14я7
К56
УДК 75(07)
Рецензенты: ст. науч. сотр., канд. физ.-мат. наук В. М. Петров
(Всесоюзный научно-исследовательский институт искусствознания Мин-
культа СССР и АН СССР), канд. искусствоведения Г. Я. Скляренко
(Институт искусствоведения, фольклора и этнографии им. М. Ф. Рыльского
АН УССР), доц., канд. техн. наук П. Е, Шпара (Харьковский институт ин-
женеров коммунального строительства)
Редакция литературы по машиностроительному комплексу
Редактор Е. В. Алексейчук
Ковалев Ф. В.
К56 Золотое сечение в живописи: Учеб. пособие.— К.: Вы-
ща шк. Головное изд-во, 1989.— 143 с, 90 ил., табл.—
Библиогр.: 77 назв.
ISBN 5—11—001336—5.
Изложены закономерности формообразования в природе и искус-
стве, зрительного восприятия и композиционного построения изобра-
жения. Показана роль золотого сечения. Даны рекомендации по прак-
тическому применению золотой пропорции при создании целостной
гармонической формы, наиболее полно выражающей содержание про-
изведения живописи и удовлетворяющей потребность человека в пре-
красном.
Для художественных институтов и училищ.
,4903020000—125
КМ211(04)-89 541-89 ББК 85.14я7
ISBN 5—11—001336—5 © Издательское объединение
«Выща школа>, 1989
Предисловие
Я хочу сократить вам путь долгих и
тяжелых исканий.
Н. П. Крымов
Опыт преподавания рисунка, живописи и композиции в художествен-
ных институтах и училищах убедительно показывает, что теоретические
положения этих дисциплин, особенно композиция, разработаны недостаточ-
но. Многие понятия и определения, положенные в основу их преподавания,
толкуются неоднозначно. Каждый художник-педагог полагается на свой
личный опыт, на опыт своих учителей и неизбежно вносит в обучение долю
субъективизма.
|
|
|
Научные знания по математике (геометрия и перспектива), физике
(свет и цвет), анатомии и физиологии человека (строение и работа глаза
и мозга), психологии (восприятие цвета и его воздействие на человека),
получаемые учащимися на занятиях по общеобразовательным предметам,
мало увязываются или не увязываются вовсе с обучением по специальности
художника.
В процессе подготовки художника большие надежды возлагаются на
природную одаренность учащихся, степень усвоения и выполнения заданий
по специальным предметам, но недооценивается роль выработки стройной
системы научных знаний и материалистического мировоззрения. Поэтому
при выходе из стен учебного заведения молодой художник не получает
прочных основ в системе понятий профессионального и мировоззренческого
характера, что отрицательно сказывается на его творческой работе.
Многие годы усилия автора данного учебного пособия были направлены
на поиски и обоснование научных, объективно обусловленных понятий тео-
рии композиции и методов построения изображения. Огромное внимание
было обращено на необходимость естественного слияния знаний и худо-
жественных навыков, чутья художника и разума. Видное место заняло рас-
смотрение закономерностей зрительного художественного восприятия, вы-
текающих из строения и работы глаза и мозга человека, связанных с ними
законов пропорции, симметрии и ритма, гармонизации формы произведения
искусства, единства формы и содержания как проявления единства мате-
риальности мира, когда мысли, идеи, чувства и деяния великих ученых и
художников, по образному выражению писателя В. А. Чивилихина ', рас-
сматриваются как сияющее цветение материи. При рассмотрении роли
пропорции и симметрии в гармонизации формы особое внимание уделено
золотому сечению.
|
|
|
Основу данной книги составляет цикл лекций «Золотое сечение в жи-
вописи», прочитанных в Киевском государственном художественном инсти-
туте и оформленных в курс по теории композиции.
Автор глубоко признателен руководству Киевского государственного
художественного института, проректору по научной работе доценту Криво-
лапову Михаилу Александровичу за неоценимую помощь, оказанную в под-
готовке учебного пособия «Золотое сечение в живописи».
1 Чивилихин В. А. Память//Роман-газета.— 1985.—№ 4.— С. 94.
Введение
Система художественного образования в СССР
имеет свою историю и традиции, заложенные Ака-
демией художеств в XVIII и XIX вв. Русское
изобразительное искусство, представленное рядом
таких выдающихся мастеров, как А. А. Иванов,
В. И. Суриков, И. Е. Репин и другие, завоевало
мировое признание. Но уже к концу XIX в. акаде-
мическая система образования устаревает, приобре-
тая черты рутинности, и не отвечает новым тре-
бованиям, которые предъявлялись искусству самой
жизнью. Художники же стремились расширить
круг тем и сюжетов своих картин, ответить на
жгучие вопросы общественной жизни. Это требова-
ло расширения средств изобразительного искус-
ства, поисков новой художественной выразитель-
ности. Академическая система художественного
образования уже не могла ответить на эти требо-
вания. Методы обучения рисунку, живописи и
особенно композиции необходимо было улучшать.
Естественные науки в то время дали объяснение
многим теоретическим вопросам: о свете и цвете,
работе мозга и строении глаза, цветоощущении
и др. Профессора Академии художеств того вре-
мени не могли ими воспользоваться для улучше-
ния художественного образования в силу собствен-
ной слабой фундаментальной подготовки. Один
только Павел Петрович Чистяков, этот учитель
учителей, посещал лекции по общей физиологии
известного ученого И. Р. Тарханова, поэтому он
многие вопросы художественной практики объяс-
нял, исходя из анатомии глаза и физиологии
зрения.
Изобразительное искусство конца XIX — начала
XX вв., переживавшее серьезный кризис, не могло
решить вопросы совершенствования художествен-
ного образования. Такое положение дел способ-
ствовало возникновению всевозможных формали-
стических теорий и направлений, вплоть до абсурд-
ных. Все это сказалось и на художественной школе.
Был забыт основополагающий принцип, изложен-
ный выдающимся художником-педагогом П. П. Чи-
стяковым и гласивший, что преподавание должно
идти не по произволу каждого художника, а по
|
|
|
законам, лежащим в самой натуре, нас окружаю-
щей, и с полными доказательствами. Педагог не
имеет права вводить ученика в заблуждение свои-
ми субъективными рассуждениями, подчинять его
личным художническим пристрастиям. Напротив,
культивировалось понятие, питаемое идеалистиче-
ской эстетикой, что для художника первичны
вдохновение и чувство. После посещения выставки
картин молодых художников в 1893 г. И. Е. Репин
писал: «Это царство развязной бездарности, анар-
хистов в живописи... Особенно пришлись по сердцу
новые правила этому легиону мазил. Учиться не
надо; анатомия — чепуха; рисунок — устарелая
каллиграфия; добиваться, переписывать — само-
уничтожение; компоновать, искать — старый рутин-
ный идиотизм...» 1
Становление советского искусства в первое де-
сятилетие после Октября шло в условиях острой
борьбы различных творческих группировок, про-
возглашавших свои декларации как единственно
правильные. Эта борьба направлений и течений
проникла и в сферу художественной педагогики,
оказав сильное влияние на обучение молодых
художников рисунку, живописи и композиции.
Была в ходу теория «свободного обучения», кото-
рая на практике приводила к отсутствию обучения.
Художники-реалисты вели настойчивую и последо-
вательную борьбу за утверждение в школе прин-
ципов реализма. Большой вклад в становление
советской художественной школы внесли Д. Н. Кор-
довский, В. Н. Мешков, К. Ф. Юон и др. В. А. Фа-
ворский читал лекции по теории композиции, кото-
рые имели большой успех у студентов и педагогов
Вхутемаса. В союзных и автономных республиках
организовывались художественные школы. Возник-
ла острая необходимость в выработке единой
системы художественного образования.
|
|
|
В 1926 г. было проведено Всесоюзное совеща-
ние по вопросам художественного образования.
Оно проходило в Москве. Доклад о состоянии
художественного образования в стране делал нар-
1 Репин И. Е. Далекое — близкое.—М., 1937.—С. 537.
ком просвещения А. В. Луначарский. Он отметил,
что в музыке есть стройная система обучения,
основанная на научной теории. Вобласти изобра-
зительного искусства дела обстоят много хуже.
Здесь не выработались законченные физико-мате-
матические теории. Подчеркивалось, что при раз-
работке теории необходимо учесть физическую
сторону, рассмотрев элементы данного искусства
всеми экспериментальными и математическими
способами, а также физиологическую сторону,
включая сюда и строение соответствующих орга-
нов, и изучение функций нервной системы и мозга.
Установки этого доклада направляли на разработ-
ку научной теории изобразительного искусства во-
обще и научной теории композиции в частности.
Основы теории музыки были заложены в глу-
бокой древности. Еще древнегреческий философ и
математик Пифагор и его ученики, которые с
большим увлечением и настойчивостью исследова-
ли гармонию, заметили, что высота звука при дан-
ном натяжении струны зависит от ее длины.
Укорочением струны вдвое получали более высо-
кий звук, еще большим укорочением — еще более
высокий и так далее. Так образовался звукоряд.
Зная длину струны (математическое основание),
количество колебаний в секунду (физическое осно-
вание), нетрудно создать физико-математические
основы теории музыки. Анатомическое строение
органа слуха также было изучено раньше, чем
устройство органа зрения. Немецкий физик, мате-
матик и физиолог Герман Гельмгольц (1821 —
1894) построил модель уха, что позволило изучить
характер воздействия звуковых волн на орган слу-
ха. Он разработал физическую и физиологическую
теорию восприятия музыкальных звуков, а в 1862 г.
издал книгу «Учение о слуховых ощущениях как
физиологическая основа для теории музыки».
В музыке фундаментальное знание науки о гар-
монии обязательно предшествует искусству компо-
зиции. В изобразительном искусстве до сих пор
держится мнение, что теория художнику вредна,
что знакомство с наукой о пропорциях не обяза-
тельно. Более того, многие считают, что знание
закона золотого сечения мешает свободному ин-
туитивному творчеству. К тому же слишком боль-
шие надежды возлагаются на натуру (нарисовать
с натуры, написать с натуры, композицию высмот-
реть в натуре). Это большое и глубокое заблужде-
ние. Научившись рисовать и писать с натуры, но
не зная теории композиции, многие художники так
|
|
|
и не становятся «композиторами», истинными твор-
цами. Мастера Древней Греции, умевшие созна-
тельно пользоваться золотой пропорцией, что в
сущности весьма просто, умело применяли ее
гармонические величины во всех видах искусства
и достигли такого совершенства строения форм,
выражающих их общественные идеалы, какое ред-
ко встречается в практике мирового искусства.
Вся античная культура прошла под знаком золотой
пропорции. Знали эту пропорцию и в Древнем
Египте.
Знание законов золотого сечения, или непре-
рывного деления, как его называют некоторые
исследователи учения о пропорциях, помогает ху-
дожнику творить осознанно и свободно. Используя
закономерности золотого деления, можно иссле-
довать пропорциональную структуру любого худо-
жественного произведения, даже если оно созда-
валось на основе творческой интуиции. Эта сторона
дела имеет немаловажное значение при изучении
классического наследия и при искусствоведческом
анализе произведений всех видов искусства.
Югославский исследователь непрерывного де-
ления Д. Петрович в книге «Теоретики пропорций»
отмечает, что в последнее время нарастает совер-
шенно естественная потребность в создании единой
теории пропорций, и золотое сечение, в связи с
этим, возбудило всеобщий интерес. Д. Петрович
перечисляет 133 источника, в которых речь идет
о пропорциях, и отсылает читателя к библиогра-
фическому справочнику по проблеме пропорциони-
рования, в котором содержится около 900 наимено-
ваний. Он делает вывод: суммарные исследования
о явлении непрерывного деления (золотого сече-
ния) в природе и искусстве предсказывают ему
большое будущее в области композиции 1.
Сейчас с уверенностью можно сказать, что зо-
лотая пропорция — это та основа формообразова-
ния, применение которой обеспечивает многообра-
зие композиционных форм во всех видах искусства
и дает основание создать научную теорию компо-
зиции и единую теорию пластических искусств.
Естественные науки уже дали нам достаточные
научные сведения о свете, глазе и мозге, зритель-
ном восприятии. Поэтому создание такой теории
на строго научных основаниях стало вполне воз-
можным.
1 Петрович Д. Теоретики пропорций.—М., 1979.—193 с.
История учения о пропорциях — это история
поисков теории гармонии и красоты. Вся античная
эстетика, а также и эстетика Возрождения искали
законы красоты в соизмеримости отдельных частей,
а также частей и целого. Эту соизмеримость в фор-
ме дают пропорции золотого сечения и симметрия.
Мы не погрешим против истины, если скажем:
все дороги ведут к золотому сечению. Человек —
лучшее, совершеннейшее творение природы — соз-
дан в пропорциях непрерывного деления. В нем
осуществилась пропорция золотого сечения как в
целом, так и в частях: в работе мозга и сердца,
строении глаза, пропорциях частей лица, руки,
кисти и всего тела.
Мы привыкли повторять, что природа — вели-
кий учитель, а художник — ученик природы. Как
понимать эти слова? Должен ли художник непре-
станно рисовать с натуры, писать сотни этюдов,
брать все готовое от природы и копировать ее,
высматривать подходящие сцены для композиции
или он должен изучать композиционные приемы
природы и законы формообразования? Должен ли
он понять, как природа из единой материи умеет
творить по единому плану разнообразные формы?
Должен ли художник творить по познанным зако-
нам природы, продолжать ее великое дело, гово-
рить на ее языке и создавать произведения по
законам гармонии и красоты? Своим трудом автор
пытается ответить на эти вопросы.
Книга посвящена золотому сечению в живопи-
си, его теоретическому пониманию и роли в прак-
тической работе живописца. Развитие нашего
изобразительного искусства и его теория сформиро-
вались таким образом, что о золотом сечении в
живописи художники знают очень мало, большей
частью понаслышке или не знают вовсе.
О применении золотого сечения в архитектуре
написано довольно много. П. Е. Шпара в книге
«Техническая эстетика и основы художественного
конструирования» указывает, что в теории архитек-
туры вопросы композиции разработаны наиболее
подробно и составляют специальный предмет тео-
рии архитектурной композиции и золотое сечение
в этой теории занимает подобающее ему место 1.
Правила золотого числа изучают не только
архитекторы, но и конструкторы, математики и
другие специалисты. В 1979 г. издательство «Про-
1 Шпара П. Е. Техническая эстетика и основы художест-
венного конструирования.— К., 1984.—С. 28.
Свещение» (М.) выпустило учебное пособие «Худо-
жественное проектирование» под редакцией
Б. В. Наумова и Е. Д. Щедрина для педагогиче-
ских институтов, где вопросу о пропорциях и золо-
тому сечению уделено определенное внимание. Но
авторы не могут сказать, почему нам приятно
смотреть на произведения искусства, в которых
выдержаны пропорции золотого сечения, почему
они производят эстетическое впечатление.
Отрадно отметить, что золотому сечению все
чаще уделяют внимание авторы трудов по вопро-
сам живописи, эстетики и наук, где оно находит
положительную оценку. «Один из видов пропорции,
так называемое «золотое сечение», широко распро-
странено в природе, используется людьми»,— ука-
зывает В. С. Корниенко в книге «О законах кра-
соты» 2. О. Я. Кочик, отмечая стремление художни-
ка В. Э. Борисова-Мусатова к такому построению
картины, при котором она будет логично органи-
зованной, подчиненной строгим закономерностям
формы, приводит примеры использования пропор-
ций золотого сечения в его картинах «Гобелен»,
«Водоем» и эскизе росписи «Осенний вечер» 3.
Много внимания рассмотрению золотого сече-
ния уделил П. И. Гаврилюк в книге «Проблема
эстетического и теория управления» 4. В капиталь-
ном труде О. Буткевича «Красота» есть слова:
«Нас пленяет стройность и уравновешенность, но
не просто механическая симметрия... нас восхи-
щает золотое сечение...» 5.
В 1982 г. издательство «Вища школа» (К.)
выпустило учебное пособие «Основы художествен-
ного конструирования». Автор пособия И. Т. Вол-
котруб в разделе «Закономерности и средства
композиции» говорит о большом значении пропор-
ций, которые определяют соразмерность и гармо-
ничность элементов формы, и подчеркивает, что
среди них особо выделяется «золотое сечение».
Форма, организованная при помощи пропорций
золотого сечения, вызывает впечатление красоты,
приятности, согласованности, соразмерности, гар-
моничности. Он отмечает также, что секрет золо-
того сечения был известен в далекой древности:
2 Корниенко В. С. О законах красоты.—Харьков, 1970.—
С. 154.
3 Кочик О. Я. Живописная система В. Э. Борисова-Муса-
това.—М., 1980.—С. 30, 128 и 139.
4 Гаврилюк П. И. Проблема эстетического и теория управ-
ления.- К., 1970.-С. 29, 60-65.
5 Буткевич О. Красота.—Л., 1979.—С 114.
египетские храмы, пирамиды, древнегреческий храм
Парфенон и статуи Фидия — все это результат
практического применения зодчими и художника-
ми отношения золотого сечения. Альбрехт Дюрер
подметил его в соразмерности человеческого тела.
С ним хорошо был знаком великий мастер Антонио
Страдивари, который использовал это соотношение
при изготовлении своих знаменитых скрипок 1
Представление о временных границах практи-
ческого применения золотого числа при создании
произведений искусства дает книга Н. А. Померан-
цевой «Эстетические основы искусства Древнего
Египта». В книге показано, что «...система пропор-
ций являлась той основой, которая обеспечивала
синтез всех видов искусства и приводила в гармо-
ничное равновесие все элементы внутри компози-
ции» 2.
В 1986 г. издана книга И. Шевелева «Принцип
пропорции» (М.), в которой обстоятельно рассмот-
рены принципы формообразования в природе и
показана роль золотого сечения.
Побудительной причиной изучения роли золото-
го сечения в живописи была потребность моей
педагогической и творческой практики. Следова-
ние педагогическим принципам П. П. Чистякова
побуждало дать себе и ученикам ясный и вразуми-
тельный ответ на все вопросы, связанные с работой
над картиной: выбор точки зрения, перспективное
и композиционное построение изображения, по-
строение колорита, организация центра внимания
и как итог — подчинение всех изобразительно-вы-
1 Волкотруб И. Т. Основы художественного конструиро-
вания.—К., 1982.—С. 38.
2 Померанцева Н. А. Эстетические основы искусства Древ-
него Египта.—М., 1985.—С. 111.
разительных средств живописи наиболее совершен-
ному выражению замысла — идее картины. С этим
связана и возможность наиболее сильного воздей-
ствия картины на зрителя.
Изучение литературы о золотом сечении может
занять у молодого художника не только многие
часы и дни, а месяцы и годы, которые так необхо-
димы ему для совершенствования художественного
мастерства. В то же время без знания учения о
золотом сечении художник может уподобиться
человеку, вслепую ищущему дверь в темной ком-
нате. Без знаний закономерностей золотого сечения
он никогда не сможет подняться до тех высот
художественного совершенства, до которых подня-
лись художники-классики. Художник, не вооружен-
ный знаниями, всегда будет в плену всяких слу-
чайностей и просчетов, которые неминуемо умень-
шат художественные достоинства его работ.
Правила золотой пропорции проявляются не
только в линейном построении изображения на
плоскости. Они распространяются на всю поверх-
ность холста при решении общего светлотного тона
картины и при построении колорита, а в итоге —
на все компоненты художественном формы. В дан-
ной книге показано, что проявление законов золо-
той пропорции, симметрии и ритма в произведениях
живописи обусловлено не их автономностью,
а всегда подчинено выявлению смысла, идеи про-
изведения, наиболее полному и ясному раскрытию
его содержания. Рассматриваются закономерности
зрительного восприятия и эмоционального воздей-
ствия на зрителя. Приводятся законы и правила
композиции, приемы построения изображения,
предложена схема общей теории изобразительного
искусства.
Глава первая
Золотое сечение и вопросы теории композиции
О золотом сечении
Золотое сечение - гармоническая пропорция
Спор о том, должна или не должна наука
вторгаться в заповедные области искусства, идет
давно. И спор этот носит явно схоластический
характер. Во все эпохи процветания искусство
вступало в союз с наукой. Художники-мыслители,
теоретики и педагоги, размышлявшие над пробле-
мами обучения молодых, всегда приходили к вы-
воду, что без науки искусство развиваться и про-
цветать не может. Художник и педагог Н. П. Кры-
мов писал: «Говорят: искусство не наука, не
математика, что это творчество, настроение и что
в искусстве ничего нельзя объяснить — глядите и
любуйтесь. По-моему, это не так. Искусство объяс-
нимо и очень логично, о нем нужно и можно знать,
оно математично... Можно точно доказать, почему
картина хороша и почему плоха» 1В. И. Суриков
утверждал, что в композиции есть какой-то непре-
ложный закон, когда в картине нельзя ничего ни
убрать, ни добавить, даже лишнюю точку поста-
вить нельзя, это настоящая математика.
Известный французский архитектор и теоретик
архитектуры XIX в. Виолле-ле-Дюк считал, что
форма, которую невозможно объяснить, никогда
не будет красивой. На дверях Сикионской школы
рисунка в Древней Греции было написано: «Сюда
не допускаются люди, не знающие геометрии». Не
следует художникам бояться математики, она
вовне и внутри нас. За кажущейся простотой и
случайностью живого восприятия окружающей дей-
ствительности скрывается математика. Когда мы
слушаем музыку, наш мозг занимается алгеброй.
Когда мы смотрим на что-либо, наш мозг занима-
ется геометрией. У человека не может возникнуть
отношение к предмету, чувство, эмоция, пока мозг
1 Крымов Н. П.—художник и педагог.—М., I960.—С. 32.
Геометрия владеет двумя сокровищами:
одно из них — это теорема Пифагора,
а другое — деление отрезка в среднем
и крайнем отношении.
И. Кеплер (1571—1630)
не произвел «измерение», сравнение этого предмета
с уже имеющимся в памяти чем-то подобным.
Впереди идет математика, а только потом возни-
кает чувство. Эту работу мозг производит мгновен-
но, потому мы ее не замечаем и не осознаем и нам
кажется, что чувство возникает сразу.
Прежде чем определить золотое сечение, необ-
ходимо ознакомиться с понятием пропорции.
В математике пропорция (лат. proportio) — это
равенство между двумя отношениями четырех ве-
личин: а: Ь = с: d. Далее, для примера обратимся
к отрезку прямой (рис. 1). Отрезок АВ можно
разделить на две равные части (/). Это будет
соотношение равных величин — АВ: АС = АВ: ВС.
Эту же прямую (2, 3) можно разделить на две
неравные части в любом отношении. Эти части
пропорции не образуют. Отношение малого отрезка
к большому или меньшего к большему есть, а со-
отношения (пропорции) нет. И, наконец, прямую
АВ(4) можно разделить по золотому сечению,
когда АВ: АС, как АС: ВС. Это и есть золотое
деление или деление в крайнем и среднем отно-
шении.
Из вышеизложенного следует вывод, что золо-
тое сечение — это такое пропорциональное гармо-
ническое деление отрезка на неравные части, при
котором весь отрезок так относится к большей
части, как сама большая часть относится к мень-
шей; или другими словами, меньший отрезок так
относится к большему, как больший ко всему,
т. е. a: b = b: с или с \Ь = Ь: а (рис. 2). Определе-
ние— деление в крайнем и среднем отношении —
становится более понятным, если мы выразим его
геометрически (рис. 3), а именно а: Ь как Ь: с.
Из рис. 3 понятно, почему астроном Иоганн
Кеплер называл золотую пропорцию продолжаю-
щей саму себя. «Устроена она так,— писал И. Кеп-
лер,— что два младших члена этой нескончаемой
пропорции в сумме дают третий член, а любые
два последних члена, если их сложить, дают сле-

|
РИС. I.
Деление отрезка прямой на равные части и по золотому се-
чению:
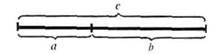
Рис. 2.
Геометрическое и алгебраическое выражение золотой пропор-
ции:
а: в =в:с или с: в =в: а
дующий член, причем та же пропорция сохраняет-
ся до бесконечности» 1.
Как видим, построение ряда отрезков золотой
пропорции можно производить как в сторону уве-
личения (возрастающий ряд), так и в сторону
уменьшения (нисходящий ряд). В последнем слу-
чае необходимо от большего отрезка вычесть мень-
ший— получим еще меньший: b — a = d, и т. д.
Практическое знакомство с золотым сечением
обычно начинают с деления отрезка прямой в зо-
лотой пропорции геометрическим способом (рис.4).
I —АВ; АС=АВ: ВС (образуется пропорция); 2, 3 — пропорция не об-
разуется; 4—АВ:АС=АС:ВС или ВС: АС=АС: АВ (золотая пропор-
ция)
1 Кеплер И. О шестиугольных снежинках.—М., 1982.—
С. 17.

|
Рис. 3.
Среднее пропорциональное или деление отрезка в крайнем и среднем отношении:
й — Ь — а; с=а+Ь

|

|
Рис. 4. Рис. 5.
Геометрическое деление отрезка прямой по золотому сечению Определение линии золотого сечения на картине геометриче-
(разработано А. Дюрером): ским способом:
ВС =0,5 АВ; CD =ВС ВС =0,5 АВ

|
Рис. 6.
Применение золотого сечения в построении картины И. Е. Репина «А. С. Пушкин на акте в Лицее 8 января 1815 года»
Из точки В восставляется перпендикуляр, равный
половине АВ. Полученная точка С соединяется
линией с точкой А. На полученной линии отклады-
вается отрезок ВС, заканчивающийся точкой D.
Отрезок AD переносится на прямую АВ. Получен-
ная при этом точка £ делит отрезок АВ в соот-
ношении золотой пропорции. Арифметически отрез-
ки золотой пропорции выражаются бесконечной
иррациональной дробью. АЕ = 0,618..., если АВ
принять за единицу, ££ = 0,382.... В практике при-
меняется округление: 0,62 и 0,38. Если отрезок АВ
принять за 100 частей, то большая часть отрезка
равна 62, а меньшая — 38 частям.
При переносе геометрического способа деления
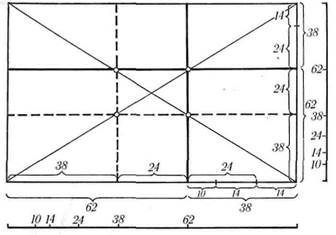
Рис. 7.
Линии золотого сечения и диагонали на картине
на картину или эскиз поступают так: половину
длины картины или эскиза откладывают на высоту
или продолжение высоты, если эскиз узкого фор-
мата. Полученную точку С соединяют с левым
нижним углом картины и т. д. (рис. 5). Линия
золотого сечения в левой части картины будет
находиться на таком же расстоянии от левого края,
как и в правой от правого (показано пунктиром).
Указанные выше две пропорции золотого деле-
ния — равные величины и неравные, при этом про-
порциональные, широко используются в искусстве.
Фигура А. С. Пушкина в картине И. Е. Репина
«А. С. Пушкин на акте в Лицее 8 января 1815 г.»
помещена художником на линии золотого сечения
в правой части картины (рис. 6). Левая часть
картины, в свою очередь, тоже разделена в про-
порции золотого сечения: от головы А. С. Пушкина
до головы Г. Р. Державина и от нее до левого
края картины. Расстояние от головы Державина
до правого края картины разделено на две равные
части линией золотого сечения. В нижней части
картины глаз улавливает деление на три равные
части. Их образуют стол в левой части картины,
нога Пушкина правее линии золотого сечения и
правый край картины.
Если необходимо найти линию золотого сече-
ния на картине или эскизе по горизонтали, то
новое деление геометрическим способом высоты
картины производить нет необходимости. Доста-
точно провести диагонали картины. Их пересече-
ния с линиями золотого сечения по вертикали
укажут точки, через которые следует провести
горизонтальные линии золотого сечения (рис. 7).
Эти линии могут понадобиться при построении пей-
зажа. Художники-пейзажисты из опыта знают, что
нельзя отводить половину плоскости холста под
небо или под землю и воду. Лучше брать или
больше неба, или больше земли, тогда пейзаж
«лучше смотрится».
Из пропорции золотого сечения вытекает, что
если высоту или ширину картины разделить на
100 частей, то больший отрезок золотой пропорции
равен 62, а меньший — 38 частям. Эти три вели-
чины позволяют нам построить нисходящий ряд
отрезков золотой пропорции: 100 — 62 = 38; 62 —
— 38 = 24; 38 — 24=14; 24— 14=10.
100, 62, 38, 24, 14, 10 — это ряд величин золотой
пропорции, выраженных арифметически. Так же
находят отрезки золотой пропорции и на картине,
если линия золотого сечения по вертикали уже
проведена (рис. 7). Переносим линию золотого
сечения в левый край картины. Расстояние между
линиями золотого сечения в середине картины рав-
но 24 частям. Отрезок, равный 24 частям, отклады-
ваем на отрезок, равный 38 частям, и получаем
остаток, равный 14 частям. Последний отрезок
накладываем на отрезок, равный 24 частям, и по-
лучаем отрезок, равный 10 частям. Все отрезки
нисходящего ряда золотой пропорции для данной
картины мы получили. Ту же операцию проводим
и с высотой картины. Полученные отрезки пере-
носим на полоску плотной бумаги или картона —
для ширины с лицевой стороны и для высоты с
оборотной. Этот простейший инструмент назовем
пропорциональной линейкой. Такая пропорцио-
нальная линейка пригодна только для данного
эскиза или эскиза такого же размера. Изготовле-
ние ее занимает несколько минут, но в дальнейшем
облегчит работу над эскизом в поисках интервалов
между фигурами или группами фигур, между
предметами, поможет найти их размеры и, в ко-
нечном итоге, гармонизовать линейное построение
картины.
Фигура А. С. Пушкина в картине Н. Н. Ге
«Александр Сергеевич Пушкин в селе Михайлов-
ском» поставлена художником на линии золотого
сечения в левой части полотна (рис. 8). Ыо и все
остальные величины по ширине вовсе не случайны:
ширина печи равна 24 частям от ширины картины,
этажерки— 14 частям, расстояние от этажерки до

Рис. 8.
Пропорции золотого деления в линейном построении картины Н. Н. Ге «Александр Сергеевич Пушкин в селе Михайловском
печи также равно 14 частям и т. д. Такие же
величины есть и в картине И. Е. Репина (см. рис. 6):
от левого края картины до головы Державина —
24 части; от стола до носка сапога правой ноги
Пушкина — 24 части. Такое же расстояние от го-
ловы Пушкина до головы военного, с восторгом
слушающего чтение поэта (его голова находится
на второй линии золотого сечения в таком же
повороте, как и голова Пушкина). От голов
Пушкина до головы молодой женщины в право
части картины, с умилением слушающей деклама-
цию, тоже — 24 части, а от ее головы до npaвого
края картины — 10 частей и т. д.
Повторение равных величин, чередование paв-
них и неравных величин в пропорциях золотое
сечения создает в картине определенный ритмиче-

|
Рис. 9.
Ряд отрезков золотой пропорции
скии строй, вызывающий у зрителя то или иное
настроение и втягивающий его в рассматривание
изображения. Порядок и последовательность этого
рассматривания предопределены художником.
Достоинство пропорции золотого сечения за-
ключено в том, что, раз поделив отрезок прямой
или сторону картины геометрическим способом,
получают отрезки любого уменьшения. В практи-
ческой же работе художника достаточно величин,
соответствующих числовым значениям 62, 38, 24,
14 и 10 (рис. 9).
Отрезки золотой пропорции нисходящего ряда
при известной величине отрезка АВ или ширине
эскиза, картины, репродукции — если мы желаем
их проанализировать, получают путем вычисления.
Например, ширина эскиза равна 14 см. Одна сотая
часть от 14 составит 0,14 см. 0,14 умножаем на
62 и получаем больший отрезок золотой пропорции,
равный 8,68 см. Следовательно, 100 частей = 14,00;
62 части = 8,68; 38 частей = 5,32; 24 части = 3,36;
14 частей = 1,96; 10 частей = 1,4 см.
Откладываем эти значения на пропорциональ-
ной линейке, как показано на рис. 7, и дальнейшую
работу над эскизом проводим с помощью этой
линейки. Интуитивное сочетается с математикой
и расчетом.
Случается так, что размер эскиза равен 10 см
(100 мм) по ширине и высоте (квадрат). Тогда
золотая пропорция на эскизе или пропорциональ-
ной линейке откладывается по линейке: 62, 38 и
24 мм. При размере картины 100x100 см посту-
пают аналогичным образом. Если же одна из сто-
рон картины равна 100 см, то, отложив на ней
с помощью линейки отрезки золотой пропорции,
проводим линии золотого сечения. Пересекаем их
диагоналями и получаем данные для нахождения
отрезков золотого сечения для другой стороны
картины, не равной 100 см, как показано на рис. 7.
Когда эскиз не очень большой, применяют ме-
тод нахождения золотых пропорций на одной из
его сторон при помощи проведения вспомогатель-
ной линии размером в 10 см (100 мм) под произ-
вольным углом к разделяемой линии (рис. 10).
На вспомогательной линии, которую проводят в
плоскости эскиза или за его пределами, отклады-
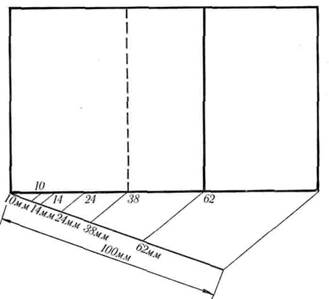
Рис. 10.
Вспомогательная линия длиной в 100 мм (10 см) для нахожде-
ния отрезков золотой пропорции на эскизе малого размера

|
Рис. 11.
Способы нахождения отрезков золотой пропорции по методу «от квадрата»:
а —квадрат; б — прямоугольник золотого сечения; в — получение точек для проведения линий золотого сечения по горизонтали; г — построение
эскиза любого формата
вают значения в миллиметрах — 62, 38, 24, 14 и 10.
Крайняя точка вспомогательной линии с
|
|
|


