 |
Определение статических характеристик случайного процесса по заданной реакции (корелляционная функция, спектральная плотность)
|
|
|
|
Ход технологического процесса характеризуется значениями фиксированного количества параметров, большая часть которых безостановочно изменяется относительно своих переменных значений. Эти изменения носят случайный характер и носят название случайных процессов. Процессы, статистические характеристики которых не изменяются во времени, называются стационарными.
Определение статистических характеристик данных процессов производится путем усреднения данных процессов различными методами. Если результаты усредненных данных процессов не зависят от применяемого способа усреднения и от вида случайного процесса, то такие случайные стационарные процессы называются - эркадическими. Основными статистическими характеристиками данных процессов являются:
математическое ожидание
 , (2.1)
, (2.1)
где Т - время реализации случайного процесса.
При определении остальных статистических характеристик случайного процесса обычно удобно сначала центрировать его, т.е. отнять от ординат от ординат процесса его среднее значение.
Вся необходимая информация для расчета линейных систем для стационарного процесса содержится в корреляционной функции:
 (2.2)
(2.2)
Физически величина корреляционной функции для некоторого момента времени τ показывает, на сколько значение, которое отстает от него на время τ.
Свойства корреляционной функции:
.  является четной функцией.
является четной функцией.
.  равна среднему значению квадрата отклонения случайного процесса от его математического ожидания и всегда больше нуля. Эту величину называют дисперсией случайного процесса.
равна среднему значению квадрата отклонения случайного процесса от его математического ожидания и всегда больше нуля. Эту величину называют дисперсией случайного процесса.
.  при
при  .
.
.  стремятся к нулю при
стремятся к нулю при 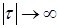 .
.
В том случае когда исследуется связь между двумя случайными процессами  и, характеристикой этой связи будет являться взаимной корреляционная функция
и, характеристикой этой связи будет являться взаимной корреляционная функция
|
|
|
 . (2.3)
. (2.3)
Величина взаимной корреляции показывает, как зависит ордината процесса  в момент времени τ+ t от ординаты процесса
в момент времени τ+ t от ординаты процесса  в момент времени t. Основные свойства
в момент времени t. Основные свойства  :
:
.  ,
,  является четной функцией.
является четной функцией.
.  стремятся к нулю при
стремятся к нулю при  .
.
Автокорреляционная функция сигнала  , которая представляет собой сумму двух случайных сигналов
, которая представляет собой сумму двух случайных сигналов  и
и  , может быть выражен через корреляционные функции слагаемых:
, может быть выражен через корреляционные функции слагаемых:
 (2.4)
(2.4)
Когда  и
и  не коррелированны между собой между собой, то взаимокорреляционные в (2.4) равны 0 и
не коррелированны между собой между собой, то взаимокорреляционные в (2.4) равны 0 и
 (2.5)
(2.5)
Если исследуются частотные характеристики объекта, то для этой цели используется соответствующая спектральная плотность 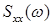 и взаимная спектральная плотность
и взаимная спектральная плотность  случайных процессов
случайных процессов  и
и  :
:
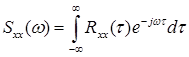 (2.6)
(2.6)
 (2.7)
(2.7)
Она является четной функцией  , для любой частоты
, для любой частоты 
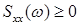 . Физически величина спектральной плотности показывает, какая доля мощности случайного процесса приходится на эту частоту.
. Физически величина спектральной плотности показывает, какая доля мощности случайного процесса приходится на эту частоту.
Общая же мощность случайного процесса может быть подсчитана как интеграл его спектральной плотности. Из обратного преобразования Фурье можно получить
 . (2.8)
. (2.8)
Тогда дисперсия будет равна суммарной мощности случайного процесса:
 . (2.9)
. (2.9)
При прохождении случайного процесса через линейную систему его характеристики изменяются. Формулы связи между характеристиками системы и характеристиками сигнала на ее входе и выходе особенно простые, когда пользоваться спектральными плотностями случайных процессов и частотными характеристиками системы.
Пусть  и
и  - соответственно случайных процессов на входе и выходе системы с амплитудно-фазовой характеристикой
- соответственно случайных процессов на входе и выходе системы с амплитудно-фазовой характеристикой  , тогда
, тогда
 (2.10)
(2.10)
Среднее значение квадрата сигнала на входе системы в соответствии с (2.9) может быть рассчитано по формуле
|
|
|
 (2.11)
(2.11)
В том случае, когда  и
и  - рациональная функция, интеграл (2.11) может быть рассчитана с помощью таблиц.
- рациональная функция, интеграл (2.11) может быть рассчитана с помощью таблиц.
Взаимная спектральная плотность процесса на входе нелинейной системы связана со спектральной плотностью процесса на входе и частотной характеристикой системы выражением:
 (2.12)
(2.12)
Выражение (2.12) соответствует связи между взаимной корреляционной функцией сигналов на входе и выходе объекта, корреляционной функцией входного сигнала и импульсной характеристикой системы выражением

Последние два выражения являются основой для определения динамических характеристик объекта статистическими методами.
ПРИЛОЖЕНИЕ 2
=0.95;=7;=5;
x=K1*rand(1,100)+K2*rand(1,100);('seed',K3);(3)(x,'b');=100;m=0:9;
z=0;
for i=1:(N-m);
z=z+x(i)*x(i+m);
end
Rxx(m+1)=z/(N-(m+1));(4)=1:10;=log(Rxx(:));=1:10;=t';=[ones(10,1),tx(:)];=inv(X'*X)*X'*Y=exp(B(1))=exp(B(1))*exp(B(2)*t)(m,Rxx,t,Wx),grid=-0.3:0.01:0.3;=-B(2)=exp(B(1))=(2*a*R0)./(a^2+w.^2);
figure(5)(w,Sxx)
ans=
a =0.0095=2.9128=18.4090

Рис.2.1 График случайного процесса

Рис.2.2 График реальной и сглаженной корреляционной функции.
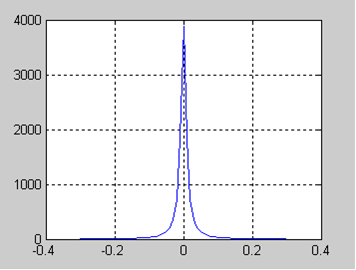
Рис.2.3 График спектральной плотности.
|
|
|


