 |
Расчет дисперсии выходной координаты АСР под воздействием случайного сигнала на ее входе
|
|
|
|
Взаимосвязь между спектральной плотностью выходного и входного сигналов объекта:
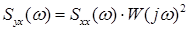 (3.1)
(3.1)
Преобразовав (3.1), получим:
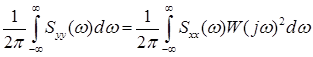 (3.2)
(3.2)
 (3.3)
(3.3)
Для вычисления (3.3) применим методы приближенного интегрирования следующего вида:
 (3.4)
(3.4)
где 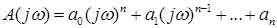 (3.5)
(3.5)
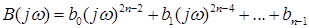 (3.6)
(3.6)
При отсутствии нулевых корней в полиноме А:
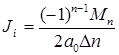 (3.7)
(3.7)
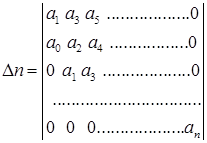 (3.8)
(3.8)
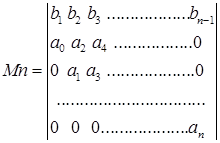 (3.9)
(3.9)
Таким образом:

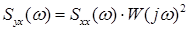 (3.10)
(3.10)
 (3.11)
(3.11)
Характеристики (3.3), (3.10), (3.11) могут быть определены по конечной реализации случайного процесса за время Т. При этом
 (3.12)
(3.12)
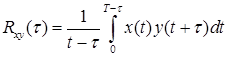 (3.13)
(3.13)
Эти выражения являются оценкой соответствующих функций (2.2) и (2.3). Если оценки соответствующих взаимокорреляционных функций равны их истинным значениям, то такие функции являются несмещенными. Вычисление данных формул по (3.12) и (3.13) приводит к несмещенным оценкам, однако их точность при больших интервалах τ может вызвать погрешность.
При применении ЭВМ для вычисления корреляционной функции необходимо получить значения ординат случайного процесса отстающих друг от друга на интервал Δt.
Количество координат:
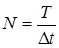
Величина Δt должна быть такой, чтобы между двумя соседними ординатами случайного процесса была линейная зависимость:
 .
.
Тогда (3.12) и (3.13) примут вид:
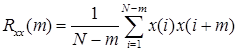 (3.14)
(3.14)
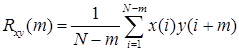 (3.15)
(3.15)

Для определения как можно более точного значения корреляционной функции можно выделить те факторы, которые влияют на полученный результат:
точность получения ординат случайного процесса зависит от класса точности регистрирующего прибора;
величина Δt
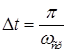
|
|
|
 - наибольшая из геометрических частот процесса. Т.к. она чаще всего независима, то примем экспериментальный метод определения Δt. По записи случайного процесса выбирают участок записи и проводят линию математического ожидания случайного процесса и определяют
- наибольшая из геометрических частот процесса. Т.к. она чаще всего независима, то примем экспериментальный метод определения Δt. По записи случайного процесса выбирают участок записи и проводят линию математического ожидания случайного процесса и определяют
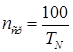
Далее  . Теперь можно выбрать максимальное значение τ
. Теперь можно выбрать максимальное значение τ
 . Определяется время реализации случайного процесса
. Определяется время реализации случайного процесса
 .
.
Полученная по формуле (3.15) корреляционная функция может быть аппроксимирована следующей кривой:
 (3.16)
(3.16)
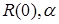 - определяются по соответствующему значению корреляционной функции.
- определяются по соответствующему значению корреляционной функции.
Преобразование Фурье от полученной зависимости дает спектральную плотность:
 (3.17)
(3.17)
ПРИЛОЖЕНИЕ 3
,clear=5.7950;=4.7036;
k=0.85;=1.1;=2.3969;=18.4090;=0.0095;=s2^2;
%Коэффициенты при соответствующих степенях
a1=a*s2^2+s1;=a*s1+1;=a;=0;
b1=0;=2*a*D*k^2;
%Вычисление дисперсии разомкнутой системы
I3=(a2*b0-a0*b1+(a0*a1*b2)/a3)/(2*a0*(a1*a2-a0*a3))=Ti*s2^2;=a*s2^2*Ti+k*Kp*Ti+Ti;=a*(k*Kp+Ti)+k;=a*k;
b0=0;=0;=2*a*D*(k*Ti)^2;=0;
%Вычисление дисперсии замкнутой системы
I4=(b0*(a2*a3-a1*a4)-a0*a3*b1+a0*a1*b2+(a0*b3/a4)*(a0*a3-a1*a2))/(2*a0*(a0*a3^2+a1^2*a4-a1*a2*a3))=
I3 =13.0390
I4 =0.3051
МОДЕЛИРОВАНИЕ АСР ПО ЗАДАЮЩЕМУ И ВОЗМУЩАЮЩЕМУ ВОЗДЕЙСТВИЯМ
Структурная схема системы с ПИ-регулятором и датчиком температуры:


Рис.4.1 График переходного процесса АСР с ПИ-регулятором и датчиком температуры при задающем воздействии
Передаточная функция датчика температуры:
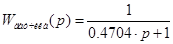
Передаточная функция объекта:

По графику переходного процесса (рис4.1.) определяем cследующие характеристики:
1) перерегулирование s = 15.5 %;
2) время регулирования tрег= 25с.
По графику видим, что ПИ-регулятор хорошо отрабатывает задающее воздействие. Статическая ошибка регулирования стремиться к пулю.
Структурная схема системы с ПИ-регулятором и датчиком температуры при возмущающем воздействии:
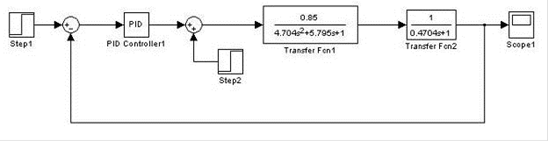

Рис.4.2. График переходного процесса при возмущающем воздействии
|
|
|
Структурная схема системы моделирования АСР по возмущающему воздействию и график переходного процесса приведены на рис(4.2).
Из него определяем cледующие характеристики:
1) перерегулирование s=29 %;
2) время регулирования tрег=30с.
ЗАКЛЮЧЕНИЕ
В курсовой работе было рассмотрено моделирование САР температуры в объекте второго порядка. В результате расчетов были построены графики экспериментальной и переходной характеристики объекта регулирования. Были найдены передаточная функция датчика и ПИ-регулятора. Определены статистические характеристики случайного сигнала по заданной реализации случайного процесса. Рассчитана дисперсия выходного сигнала разомкнутой и замкнутой АСР при воздействии случайного сигнала на входе АСР.
Все проделанные расчеты были выполнены в пакете MATLAB 6.5
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Макаров И.М., Менский Б.И. Линейные автоматические системы.- М., Машиностроение, 1982г.
2. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования.- СПб, «Профессия», 2000г.
3. Дудников, Балакирев.“Экспериментальные исследования динамических характеристик промышленных объектов” 1972г.
4. Ильин О.П., Анхимюк В.Л. Основы технической кибернетики.- Мн., 1975г.
. ”Наладка средств автоматизации и АСР” под редакцией Клюева В.С. 1990г.
6. Кузьмiцкi I.Ф., Кобрынец В.П., Аŷсяннiкаŷ А.В. Мадэляванне аб’ектаŷ i сiстэм кiравання: Вучэбны дапаможнiк для студэнтаŷ ВНУ спецыяльнасцi «Аŷтаматызацыя тэхналагiчных працэсаŷ i вытворчасцяŷ». - Мн.: БГТУ, 2003г.
|
|
|


