 |
Теоретическое исследование. Возможности создания биолазера
|
|
|
|
ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ
ВОЗМОЖНОСТИ СОЗДАНИЯ БИОЛАЗЕРА
НА ФРЕЛИХОВКИХ МОДАХ [3]
В данной главе обсуждается и аналитически рассматривается возможность создания перевозбужденного состояния основной (выделен-ной) коллективной Фрелиховской моды за счет когерентного резо-нансного взаимодействия электромагнитного (амплитудно-модулиро-ванного) излучения с Фрелиховским осциллятором. В рамках по-нятий лазерной физики речь идет о создании инверсной заселенности между квантовыми уровнями выделенной колебательной моды и, в итоге, о реализации “in vitro-in vivo” суперфлуоресценции и лазерной генерации с использованием в качестве рабочих тел молекул ДНК, РНК, белков, а также таких надмолекулярных структур, как рибосомы, полирибосомы и хромосомы.
Подчеркнем, что в отличие от Фрелиховского подхода, в котором подразумевается квазинеравновесное состояние (колебательная температура выделенной моды превосходит таковую “тепловой бани” Tvib> Teq> 0, т. е. колебания квазиравновесны), в данной работе оценены условия, при которых система рассматриваемых биосубстратов инвертирована (Tvib< 0), что прямо связано с созданием инверсной населенности.
Итак, Фрелиховская мода моделируется двухуровневой квантовой системой (уровень 1 основное состояние, 2 верхнее), возбуждаемой резонансным амплитудно-модулированным электрическим полем
E( t)=Eog(t)сoswt , (1)
где Eo амплитуда напряженности поля, g(t) модуляционный фактор, w=w21 (w21 частота перехода 2®1).
Процесс возбуждения колебаний моды описывается уравнением Больцмана для матрицы плотности:

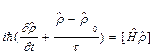 , (2)
, (2)
где оператор гамильтона в дипольном приближении имеет вид: 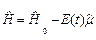
|
|
|
где Ho= 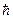 w21
w21 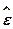 гамильтониан изолированной двухуровневой системы, оператору
гамильтониан изолированной двухуровневой системы, оператору 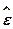 соответствует матрица с элементами
соответствует матрица с элементами 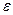 11=
11= 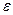 12=
12= 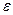 21=0,
21=0, 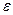 22=1,
22=1, 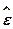 оператор прекции индуцированного дипольного момента осциллятора на направление поля,
оператор прекции индуцированного дипольного момента осциллятора на направление поля, 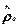
 равновесная матрица плотности,
равновесная матрица плотности, 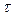 феноменологически введенное время релаксации (для диагональных элементов
феноменологически введенное время релаксации (для диагональных элементов 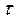 =T1, для недиагональных T2).
=T1, для недиагональных T2).
Уравнению Больцмана (2) эквивалентна следующая система уравнений для элементов матрицы плотности ( 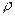 ik; i, k=1, 2):
ik; i, k=1, 2):
i 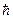 (
( 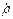 11+(
11+( 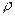 11 1)/T1)= E(t)(
11 1)/T1)= E(t)( 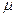 21
21 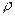 12 -
12 - 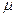 12
12 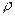 21),
21),
i 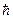 (
( 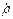 12+
12+ 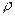 12/T2)= -
12/T2)= - 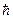
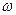 21
21 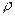 12-E(t)
12-E(t) 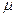 12(
12( 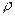 22 -
22 - 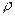 11), (3)
11), (3)
i 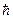 (
(  21+
21+ 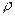 21/T2)= +
21/T2)= + 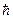
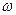 21
21 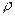 21+E(t)
21+E(t) 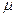 21(
21( 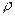 22 -
22 - 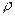 11)
11)
с учетом уровня нормировки
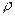 22+
22+ 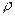 11=1 (4)
11=1 (4)
Нетрудно показать, что система (3) может сводиться к уравнению (при выкладках вторыми гармониками ~exp(2i 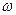 21t) пренебрегалось):
21t) пренебрегалось): 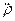 22+
22+ 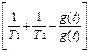
 22+
22+ 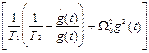
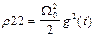

 22 (0) =
22 (0) = 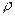 22 = 0, (5)
22 = 0, (5)
где 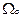 =Eo
=Eo 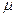 21/
21/ 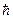 частота Раби. Заметим, что амплитудная модуляция поля приводит не только к модуляциям частоы Раби, но и к модуляции “коэффициента трения” осциллятора.
частота Раби. Заметим, что амплитудная модуляция поля приводит не только к модуляциям частоы Раби, но и к модуляции “коэффициента трения” осциллятора.
Ниже рассматривается случай T1=T2=T. Можно показать, что уравнение (5) допускает точное решение для произвольной функции g(t):
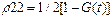 (6)
(6)
G(t)= 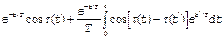

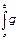 (t’)dt’ (7)
(t’)dt’ (7)
Рассмотрим случай периодической модуляции амплитуды напряженности поля
g(t)=cos 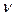 t. (8)
t. (8)
Если период модуляции T 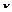 =2
=2 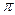 /
/ 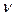 короче времени релаксации (T
короче времени релаксации (T 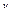 < < T), то для времени T
< < T), то для времени T 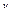 < < t< < T усреднение (6) за период T
< < t< < T усреднение (6) за период T 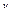 дает:
дает:
< 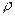 22> =1/2
22> =1/2 
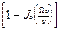
 (9)
(9)
и, соответственно, (4):
< 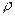 11> =1/2
11> =1/2 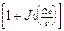 ,
, 
где 
 функция Бесселя нулевого порядка, так что для разности населенностей уровней 2 и 1 имеем
функция Бесселя нулевого порядка, так что для разности населенностей уровней 2 и 1 имеем
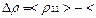
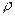
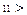 =
= 
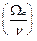 . (10)
. (10)
Из (10) четко следует, что в диапазонах параметра 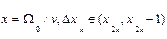 , где k=1, 2,.. и
, где k=1, 2,.. и 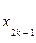 корни функции Бесселя, вероятность заселения уровня 2 превосходит таковую для уровня 1. Другими словами, мы имеем перевозбужденное инвертированное состояние осциллятора, что является необходимым условием для создания условий лазерной генерации (
корни функции Бесселя, вероятность заселения уровня 2 превосходит таковую для уровня 1. Другими словами, мы имеем перевозбужденное инвертированное состояние осциллятора, что является необходимым условием для создания условий лазерной генерации ( 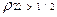 ). Ситуация здесь аналогична процессу раскачивания маятника с пульсирующей точкой подвеса (маятник Капицы, классическое рассмотрение[29]).
). Ситуация здесь аналогична процессу раскачивания маятника с пульсирующей точкой подвеса (маятник Капицы, классическое рассмотрение[29]).
|
|
|
Для больших времен, t> > T, функция G(t), входящая в соотношение (6), имеет вид:
G(t)=P(t)cos  + Q(t)sin
+ Q(t)sin 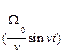 ,
,
P(t)= 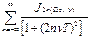
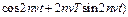
Q(t)=2 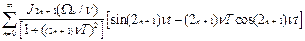 , (11)
, (11)
где J функция Бесселя соответствующего порядка.
Из (11) следует важный вывод: когерентный механизм взаимодействия Фрелиховских мод с резонансным амплитудно-модулированным полем обусловливает незатухающие колебания диагональных элементов матрицы плотности для времен t, превосходящих времена релаксации системы, причем частоты пульсаций кратны частоте амплитудной модуляции 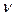 .
.
Усредняя (11) за период T 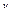 , получаем
, получаем
< G(t)> = 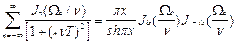 , (12)
, (12)
где x= 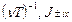 функции Бесселя мнимого порядка (i мнимая единица). В частном случае, когда период модуляции T
функции Бесселя мнимого порядка (i мнимая единица). В частном случае, когда период модуляции T 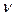
 короче времени релаксации T, x < < 1,
короче времени релаксации T, x < < 1,
< 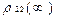 > =1/2
> =1/2 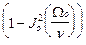 , <
, < 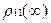 > =1/2
> =1/2 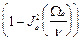 , (13)
, (13)
так что
< 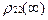 > <
> < 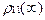 > = -
> = - 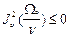 . (14)
. (14)
В данном случае эффект инверсии не реализуется.
Рассмотрим случай, когда закон модуляции задается соотношением
g(t)=1+ 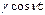 . (15)
. (15)
По аналогии с предыдущим для функции G(t), входящей в соотношение (6), можно получить (T 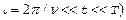 .
.
G(t)= 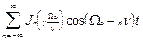 . (16)
. (16)
Из (16) видно, что спектр пульсаций диагональных матричных элементов 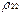 и
и 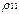 включает, кроме частоты Раби, “стоксовые” и “антистоксовые” комбинационные частоты
включает, кроме частоты Раби, “стоксовые” и “антистоксовые” комбинационные частоты 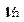
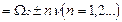 . Допустим для определенных n выполнено условие
. Допустим для определенных n выполнено условие 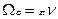 , т. е.
, т. е.
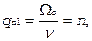 (17)
(17)
тогда, как следует из (16), постоянная составляющая для вероятностей 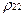 и
и 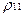 сдвигается. Динамическому состоянию равновесия при этом соответствуют величины:
сдвигается. Динамическому состоянию равновесия при этом соответствуют величины:
< 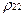 > =1/2
> =1/2 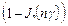 , <
, < 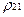 > =1/2
> =1/2 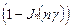 , (18)
, (18)
так что 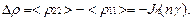
Эффект инверсии ( 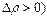 реализуется при условии
реализуется при условии
 . (19)
. (19)
Если параметр глубины модуляции 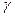 лежит в диапазонах, где значения функции Бесселя
лежит в диапазонах, где значения функции Бесселя  отрицательны, то реализуется режим перевозбуждения системы (информационных биомакромолекул и надмолекулярных структур).
отрицательны, то реализуется режим перевозбуждения системы (информационных биомакромолекул и надмолекулярных структур).
Таким образом, высказана идея принципиальной возможности создания биолазеров на Фрелиховских модах in vitro, а также инициации таких процессов в живой клетке в дополнение (или коррекции) к известным естественным лазероподобным процессам в биосистемах. Показано, что в определенных условиях в случае когерентного (резо-нансного) взаимодействия амплитудно-модулированного внешнего электромагнитного излучения с Фрелиховской модой система информационных биоструктур может существовать в перевозбужденном состоянии, что является необходимой предпосылкой для создания знаконесущих биолазеров.
|
|
|
Необходимо отметить, что описанный выше механизм формирования биолазеров на основе молекул ДНК позволяет подойти к попытке реализации еще одной фундаментальной гипотезы Фрелиха о возможности перекачки энергии kТ внутриклеточной жидкости в энергию электрических колебаний в молекуле ДНК[30]. В соответствии с этой гипотезой стохастические тепловые колебания kТ раствора могут резонансно взаимодействовать (в определенном интервале частот) с колебательными модами молекулы ДНК, и благодаря тому, что как молекула ДНК, так и молекулы белков представляют собой распределенные нелинейные колебательные структуры, часть энергии может группироваться в низкочастотных модах этих молекул. Иными словами, молекула ДНК в растворе может частично преобразовывать энергию колебаний kТ в энергию собственных мод. Заметим, что даже в рамках предложенного квазили-нейного подхода проблема перекачки тепловой энергии раствора может быть сведена к механизму затухания квантового осциллятора, который был предложен А. Пиппардом[31]. C учетом этого в уравнение Шредингера вводится комплексный потенциал, интерпретирующий передачу энергии осциллятора большому числу мод расширяющегося сферического резонатора. Если размеры этого резонатора конечны, как в случае с живой клеткой, то возникнет резонансный обмен энергии между модами kТ раствора и электрическими модами молекулы ДНК. Эти рассуждения также говорят в пользу того, что и в водно-жидкокристаллическом электролите клеточно-тканевого пространства биосистемы генетические молекулы могут функционировать как биолазеры.
Надо указать на существенное обстоятельство относительно принципиальной возможности реализации возбуждения Фрелиховских мод “in vitro” по биохимическому пути, а именно за счет энергии гидролиза АТФ и других нуклеозид-трифосфатов, а также за счет других макроэргических соединений живой клетки. В данном случае мы будем искусственно повторять то, что эволюционно и (или) иным путем дано биосистемам как основная информационная и, может быть, энергетическая фигура. Эта часть наших исследований ставит определенные нравственные и этические проблемы применения биолазеров.
|
|
|
АНТЕННАЯ МОДЕЛЬ
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ [16]
Как уже неоднократно отмечалось, функционирование ряда биологических макромолекул (в частности, ферментов) и других биологических соединений во многом определяется процессами, происходящими в активных центрах, окруженных биополимерными цепочками, имеющими знаковую топологию. Исходя из такого представления о структуре информационных биомакромолекул, естественно предположить, что их взаимодействие с физическими полями внешних по отношению к биосистеме и внутренних (организменных) излучений приводит к возбуждению дипольно-активных колебаний мономеров, формирующих указанную цепочку, а те, в свою очередь, индуцируют колебания в активном центре. Иными словами, такая система будет работать как своеобразная антенна. Эти возбужденные колебания способны привести к переходу биомакромолекулы в другое конформационное (топологическое, знаковое) состояние.
Подобная концепция в принципиальном плане адекватна целому ряду функционально высокозначимых биомакромолекул, например, хлорофилла, гемоглобина, миоглобина и т. д. Эти макромолекулы объединяются двумя структурными качествами: 1) в их геометрическом центре расположен ион (в случае хлорофилла - ион магния, в случае гемоглобина - ион железа); 2) около иона симметрично расположены 4 пиррольных кольца (псевдоплоская структура).
Другими типами биополимеров, соответствующих антенной модели, могут быть cравнительно простые циклы типа валиномицина (переносчик ионов калия) и сложные надмолекулярные структуры хромосом, ДНК которых содержит высокоорганизованные ассоциаты таких металлов, как магний, кальций, никель, кобальт, медь, железо, цинк и др. При этом роль их неясна и сводится исследователями, в основном, к нейтрализации ОН-групп остатков фосфорной кислоты полинуклеотида. Представляется, что функции металлов в ДНК и РНК существенно более широкие и реализуются по линии знакового и (или) энергетического взаимодействия с эндогенными и экзогенными по отношению к биосистеме физическими полями. То же относится и к белкам, не содержащим порфириновый центр, но специфическим образом связывающим металлы. Например, таковыми можно считать сайт-специфические белки с доменами типа “цинковых пальцев”, участвующими в регуляции генов, подчас очень далеко отстоящих от этих управляющих белков. Атомы металлов ДНК и белков могут резонансно взаимодействовать по электромагнитным каналам в рамках понятий антенной модели. Еще раз обозначим понятие антенной модели.
|
|
|
Внешняя энергия (в частности, связанная с резонансным взаимодействием крайне высокочастотных электромагнитных излучений с белками) поступает на периферию, т. е. на ансамбль субъединиц (не обязательно идентичных по структуре). В результате активной “беседы”, предопределенной биохимическими связями, между периферийными акцепторами (получившими закодированную энергию) и центром-ассоциатом (в данном случае ионом металла гемсодержащих белков), последний получает энергию (информацию), что и вызывает биологическое действие. Степень реакционной способности биомакромолекул существенно зависит от уровня возбуждения центральных субъединиц. Рассмотрим в деталях потенциальные механизмы волновых взаимодействий физических полей и активных центров информационных биомакромолекул в рамках предлагаемой нами антенной модели.
В качестве простейшей модели для иллюстрации антенного эффекта рассмотрим двумерную замкнутую (циклическую) цепочку мономеров. В центре цикла расположен активный центр, связанный с мономерами цепочки диполь-дипольным взаимодействием.
Обозначим координатные смещения мономеров через 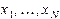 , а смещение активного центра через
, а смещение активного центра через 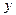 . Для потенциальной функции имеем:
. Для потенциальной функции имеем:
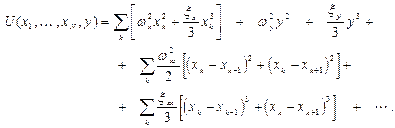 (1)
(1)
Первые два члена в (1) соответствуют колебаниям мономеров (второй член учитывает ангармонизм); последние два члена отвечают за связи между мономерами, Остальные члены отвечают за связи между мономерами и активным центром.
Уравнения движения запишем в виде:
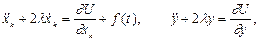 (2)
(2)
где 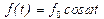 внешняя монохроматическая сила, действующая только на мономеры,
внешняя монохроматическая сила, действующая только на мономеры,  коэффициент затухания, введенный феноменологически (простоты ради принят одинаковым и для мономеров, и для активного центра).
коэффициент затухания, введенный феноменологически (простоты ради принят одинаковым и для мономеров, и для активного центра).
С учетом (1), система уравнений (2) приобретает вид:
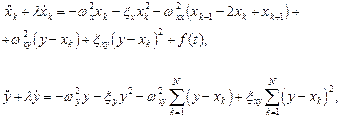 (3)
(3)
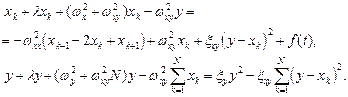 (4)
(4)
Введем общую координату для ансамбля мономеров
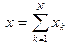 . (5)
. (5)
тогда система уравнений (4) в линейном приближении приобретает вид:
 (6)
(6)
где:
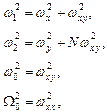
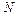 число мономеров.
число мономеров.
С учетом (5) имеем 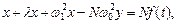 (7. 1)
(7. 1)
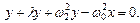 (7. 2)
(7. 2)
Из (7. 2) следует 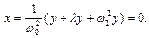 (8)
(8)
Подстановка (8) в (7. 1) дает
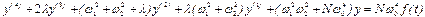 .
.
(9)
Соответствующее характеристическое уравнение имеет вид (после подстановки 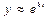 в однородное уравнение):
в однородное уравнение):
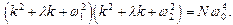 (10)
(10)
Обозначив 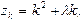 имеем
имеем
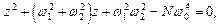
так что
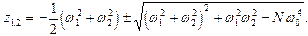 (11)
(11)
В дальнейшем предполагается выполнение неравенств:
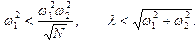 (12)
(12)
Первое условие соответствует случаю слабой связи между мономерами и активным центром, второе - малому затуханию мономерных осцилляторов.
Для собственных значений имеем
 , (13)
, (13)
где введены коллективные частоты:
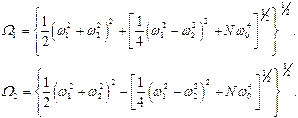 (14)
(14)
Нас интересуют вынужденные колебания (внешняя сила 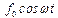 ):
):
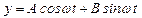 . (15)
. (15)
Подстановка (15) в (9) и приравнивание соответствующих коэффициентов при 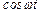 и
и 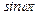 дают систему алгебраических уравнений:
дают систему алгебраических уравнений:
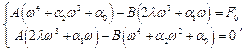
где:
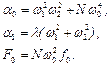
В результате получаем 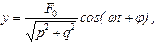
где 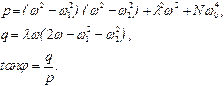
После несложных, но громоздких преобразований для вынужденных колебаний активного центра получаем:
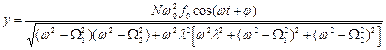 . (16)
. (16)
Из (16) видно, что наибольшая амплитуда вынужденных колебаний активного центра достигается в условиях коллективного резонанса: либо 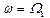 , либо
, либо 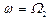 .
.
В любом из этих случаев для амплитуды вынужденных колебаний имеем:
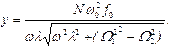 (17)
(17)
Из (17) следует, что наибольший эффект резонансной раскачки активного центра достигается при большем числе периферийных субъединиц “антенны”, при более высоком значении коэффициента связи активного центра с мономерами, при наименьшем коэффициенте затухания и при наименьшем дисбалансе коллективных мод.
Нетрудно определить и “хореографию” (динамику вынужденных колебаний) отдельных мономерных единиц. В соответствии с (6) уравнение для k -го мономера запишем в виде:
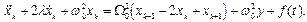 (18)
(18)
Вводя коллективные координаты
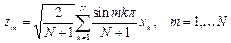
и применяя метод линейной алгебры, получаем для вынужденных колебаний мономеров:
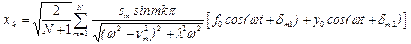 ,
,
(19)
где:

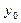 ‑ определяется из (16).
‑ определяется из (16).
Таким образом, в рамках антенной модели наибольший эффект воздействия внешнего монохроматического поля 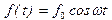 ре-ализуется в условиях коллективного резонанса:
ре-ализуется в условиях коллективного резонанса:
 .
.
Повторяя рассуждения раздела 2, можно сделать также следующие выводы:
1) При реализации амплитудной модуляции внешнего сигнала имеют место дополнительные возможности резонансного воздействия на биомакромолекулы на частотах:
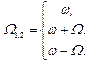
2) Учет нелинейности при квадратичной связи для монохроматического сигнала привносит дополнительный резонанс на второй гармонике 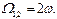
3) Учет нелинейности при амплитудной модуляции определяет еще ряд резонансных возможностей:
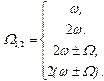
|
|
|


