 |
Пункт 2. Устранение цепных правил.
|
|
|
|
Цепное правило – это правило вида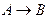 
, где 
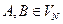. Цепные правила могут быть причиной нежелательных свойств грамматики, таких, например, как циклы. Алгоритм устранения цепных правил осуществляет замещение правой части каждого цепного правила, используя для этого не цепные правила.
АЛГОРИТМ:
Вход: КС-грамматика 
без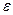 
-правил.
Выход: Эквивалентная КС-грамматика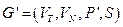 
без цепных правил.
1. Для каждого нетерминала 
вычислить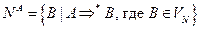 
:
1.1. Положить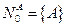 
.
1.2. Вычислить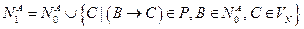 
.
1.3. Если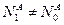 
, то положить 
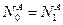и перейти к пункту 1.2; иначе положить 
.
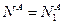2. Построить множество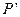 
так: если 
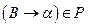не является цепным правилом 
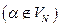, то включать в 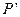правило 
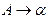для каждого , такого, что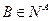 
, то есть 
.
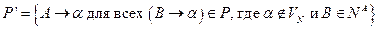Пункт 3. Левая факторизация правил.
Левую факторизацию можно выполнять для правил грамматики, определяющих один и тот же нетерминал и имеющих одинаковое начало (префикс) правых частей. Цель такого преобразовании – устранение одинаковых префиксов. При проведении левой факторизации выполняются действия, подобные вынесению за скобки общего левого множителя в алгебраических выражениях. Алгоритм преобразования состоит в следующем.
Вход: КС-грамматика .
Выход: Эквивалентная КС-грамматика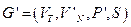 
без одинаковых префиксов в правых частях правил, определяющих нетерминал.
1. Записать все правила для нетерминала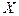 
, имеющие одинаковые префиксы 
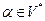, в виде одного правила с альтернативами (вариантами):
;
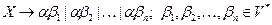2. Вынести за скобки влево префикс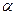 
каждой строки-альтернативы: 
.
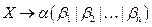3. Обозначить новым нетерминалом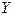 
выражение, оставшееся в скобках: 
.
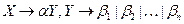4. Пополнить множество нетерминалов новым нетерминалом 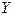и заменить правила, подвергшиеся факторизации, новыми правилами для 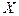и .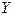
5. Повторить пункты 1 – 4 для всех нетерминалов грамматики, для которых это возможно и необходимо.
|
|
|
Пункт 4. Устранение прямой левой рекурсии.
Нетерминал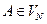 
называют рекурсивным, когда существует вывод 
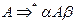, где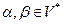 
. Если указанный вывод получается за один шаг (имеется правило 
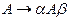), то говорят о прямой рекурсии. Если требуется более одного шага, то имеет место косвенная рекурсия (или рекурсивный цикл). В случае 
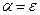рекурсию называют левой, а в случае 
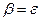- правой. Частный случай 
соответствует понятию самовложения. Если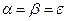 
, то получаем цикл 
.
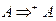При устранении рекурсии один вид рекурсии заменяется на другой, например, вместо левой рекурсии появляется правая. В приложениях теории формальных грамматик значительные неудобства часто создает именно левая рекурсия. Рассмотрим алгоритм устранения прямой левой рекурсии. Отметим, что если имеется несколько рекурсивных правил для одного нетерминала , то можно свести их к одному рекурсивному правилу путем левой факторизации. Возможна и последовательная обработка каждого из рекурсивных правил для .
Вход: КС-грамматика .
Выход: Эквивалентная КС-грамматика 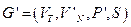без прямой левой рекурсии.
1. Вынести из грамматики все правила для рекурсивного нетерминала :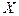
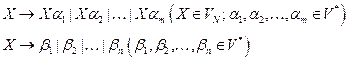
2. Ввести новый нетерминал 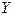так, чтобы он описывал любое окончание строки, порождаемой рекурсивным нетерминалом :
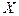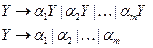
3. Заменить в рекурсивном правиле для 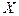правую часть, используя нетерминал 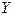и все не рекурсивные правила для 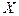, так, чтобы генерируемый язык не изменился:
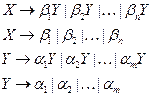
4. Пополнить множество нетерминалов грамматики новым нетерминалом 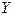. Пополнить множество правил грамматики правилами, полученными в пункте 3.
5. Повторить действия пунктов 1 – 4 для всех рекурсивных нетерминалов грамматики, после чего полученные множества нетерминалов и правил принять в качестве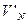 
и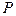 
.
Замечание: если 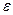-правила не будут помехой в грамматике, то в пункте 2 алгоритма можно применить для 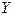правила
.
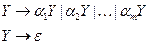Тогда в пункте 3 будут получены такие правила:
|
|
|
.
|
|
|
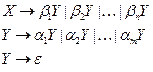