 |
Пункт 1. Определение МП-автомата.
|
|
|
|
Подобно тому, как регулярные языки можно распознавать конечным автоматом, КС-языки можно распознавать с помощью автомата с магазинной памятью, или МП-автомата. Последний эквивалентен конечному автомату, который снабжен рабочей памятью магазинного типа, то есть стеком.
МП-автомат читает входной символ, замещает верхний символ стека строкой символов и переходит в новое состояние. Новое состояние определяется прочитанным символом и содержимым вершины стека. МП-автомат принимает строку, если после ее прочтения автомат находится в заключительном состоянии.
Формально МП-автомат можно 
можно представить в виде семерки:
, где
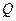- конечное множество состояний автомата;
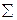- конечный входной алфавит;
- конечный магазинный алфавит;
- магазинная функция, отображение множества 
в множество всех подмножеств множества 
;
- начальное состояние автомата, 
;
- символ, который находится в магазине в начальный момент, 
;
- множество заключительных состояний автомата, 
.
Конфигурацией МП-автомата называется тройка
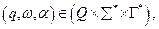где
- текущее состояние автомата;
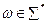- часть входной строки, первый символ которой находится под входной головкой;
- содержимое магазина.
Шаг работы МП-автомата представим в виде отношения |- на конфигурациях. Если одним из значений магазинной функции 
является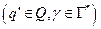 
, то можно писать 
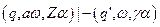. Это общая запись, которая подразумевает частные случаи.
1. Случай 
. Автомат находится в текущем состоянии 
, читает входной символ 
, имеет в вершине стека символ 
. Он переходит в очередное состояние 
, сдвигает входную головку на ячейку вправо и заменяет верхний символ строкой 
магазинных символов. Вариант 
означает, что удаляется из стека.
|
|
|
2. Случай 
. Отличается от случая 1 тем, что входной символ просто не принимается во внимание, и входная головка не сдвигается. Такой шаг работы МП-автомата называется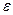 
-шагом, причем 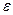-шаг может выполняться даже после завершения чтения всей входной строки.
Начальной конфигурацией МП-автомата называется конфигурация 
, а заключительной – конфигурация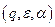 
, где 
. В заключительном состоянии входная строка полностью прочитана. Таким образом, МП-автомат допускает входную строку 
, если существует путь по конфигурациям
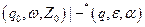
для некоторых и . Значит, язык 
, распознаваемый (принимаемый) МП-автоматом , формально можно определить так:
.
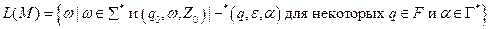Пункт 2. Разновидности МП-автоматов.
Иногда определяют МП-автомат, который принимает строку, если после завершения ее чтения стек автомата будет пуст. В этом случае нет необходимости выделять множество заключительных состояний , а описание заключительной конфигурации имеет вид 
, где . Говорят, что такой МП-автомат принимает строку языка опустошением магазина.
МП-автомат называют детерминированным (ДМП-автоматом), если, находясь в любой конфигурации, он может выбрать не более одной следующей конфигурации. Это означает, что при любых значениях , 
и 
(
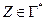для расширенного автомата) магазинная функция 
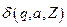имеет не более одного значения. В противном случае МП-автомат является недетерминированным.
Существует соответствие КС-грамматик и МП-автоматов, которое можно сформулировать так: существуют КС-языки, МП-автоматы и расширенные МП-автоматы, определяющие один и тот же КС-язык.
Пункт 3. Взаимосвязь МП-автоматов и КС-грамматик.
Построение МП-автомата.
По заданной КС-грамматике, генерирующей некоторый язык , можно построить МП-автомат, принимающий этот язык. Будем строить автомат, выполняющий левосторонний разбор. Такой автомат должен строить вывод строки, начиная с аксиомы грамматики. Используем стек для размещения текущей сентенциальной формы, первоначально это аксиома. Очередная сентенциальная форма получается заменой верхнего нетерминала стека. Пусть, кроме того, автомат обладает только одним состоянием и принимает входную строку опустошением магазина. Описанный МП-автомат можно построить следующим образом.
|
|
|
Вход: КС-грамматика 
.
Выход: МП-автомат такой, что 
.
1. Положить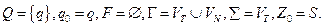 
2. Для каждого правила вида 
, где 
, сформировать магазинную функцию вида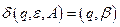 
. Эти функции предписывают замещать нетерминал в вершине стека по правилу грамматики.
3. Для каждого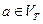 
сформировать магазинную функцию вида 
, которая выталкивает из стека символ, совпадающий с входным, и перемещает читающую головку. Эти функции обеспечивают опустошение стека.
|
|
|
