Применение матричных игр в маркетинговых исследованиях

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ имени К.Г. РАЗУМОВСКОГО (Первый казачий университет)»

(ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)»)

Башкирский институт технологий и управления (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Московский государственный университет технологий и управленияимени К.Г. Разумовского (Первый казачий университет)»БИТУ (филиал) ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)»

 

Теория ИГР

Методические рекомендации по выполнению контрольных работ для бакалавриата заочной формы обучения

 

080100.62 по направлению Экономика

 

 

 

Содержание дисциплины

Раздел 1. Задачи принятия решений. Многокритериальная оптимизация.

Проблема принятия решений в условиях антагонистического конфликта. Принятие решений в условиях риска. Принятие решений в условиях неопределенности. Принятие решений в условиях полунеопределенности.

Многокритериальная оптимизация.

Раздел 2.Антагонистические игры.

Задачи теории игр в экономике. Основные понятия и определения теории игр. Классификация игр.

Матрица выигрышей (платежная матрица, матрица игры). Чистые стратегии игроков. Соотношение между матрицами выигрышей игроков А и В в антагонистической игре. Формирование матрицы выигрышей.

Максиминный и минимаксный принципы игроков. Показатель эффективности чистой стратегии игрока А и показатель неэффективности чистой стратегии игрока В. Максимин и минимакс. Нижняя и верхняя цены игры в чистых стратегиях. Максиминные и минимаксные стратегии.

Решение матричных игр с седловой точкой. Устойчивые и неустойчивые ситуации. Ситуации, удовлетворительные для игроков. Равновесная ситуация. Седловая точка игры (седловая точка функции игры). Седловая точка матрицы игры. Свойства равнозначности и взаимозаменяемости седловых точек.

Цена игры в чистых стратегиях. Оптимальные стратегии. Полное и частное решение игры в чистых стратегиях. Соотношения между множествами оптимальных и максиминных (минимаксных) стратегий.

Раздел 3. Решение игр в смешанных стратегиях.

Смешанные стратегии. Определение. Геометрическая интерпретация множества смешанных стратегий. Определение функции выигрыша в смешанных стратегиях и формулы ее представления. Показатель эффективности смешанной стратегии игрока А. Показатель неэффективности смешанной стратегии игрока В. Нижняя и верхняя цены игры в смешанных стратегиях.

Решение игры в смешанных стратегиях. Цена игры в смешанных стратегиях. Оптимальные смешанные стратегии. Полное и частное решение игры в смешанных стратегиях. Основная теорема теории игр Дж. Фон Неймана. Критерии и свойства оптимальных стратегий. Геометрическая интерпретация множества оптимальных стратегий. Активные стратегии.

Редуцирование игр. Принцип доминирования. Разбиение матрицы игры на подматрицы со специальным свойством. Изоморфные и аффинные преобразования игр.

Аналитическое и геометрическое решение игр 2´2, 2´ n, m ´2.

Решение игры m ´ n методом Шепли-Сноу.

Решение игры m ´ n приближенным методом Брауна-Робинсон.

Раздел 4. Взаимосвязь матричных игр и линейного программирования.

Взаимно двойственные задачи линейного программирования. Приведение антагонистической игры к паре взаимно двойственных стандартных задач линейного программирования. Симплекс-метод и метод последовательного улучшения плана.

Раздел 5. Игры с природой.

Определение игры с природой. Критерии Байеса и Лапласа в чистых и смешанных стратегиях. Критерий Вальда, максимаксный критерий, критерий Гурвица относительно выигрышей в чистых и смешанных стратегиях. Критерий Сэвиджа, миниминный критерий, критерий Гурвица относительно рисков в чистых и смешанных стратегиях.

Примеры решения задач

Графическое решение игр вида (2 x n) и (m x 2)

 

Графический метод применим к играм, в которых хотя бы один игрок имеет только две стратегии. Рассмотрим игру (2 х п), см. табл. 31.2.

 

 

Предполагаем, что игра не имеет седловой точки.

Обозначим: х ₁ — вероятность применения первым игроком 1-й стратегии, x ₂ — вероятность применения первым игроком 2-й стратегии, причем х ₂ = 1 — x ₁; y ₁ — вероятность примене­ния вторым игроком 1-й стратегии, у ₂ — вероятность приме­нения вторым игроком 2-й стратегии и т.д., у_n — вероятность применения вторым игроком п -й стратегии.

Ожидаемый выигрыш первого игрока при применении вто­рым 1-й стратегии составит

 

 

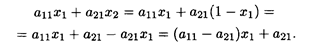
Аналогично найдем ожидаемые выигрыши первого игрока при применении вторым игроком 2, 3,..., n -й стратегий. Полу­ченные данные поместим в табл. 31.3.

 

 

Из таблицы видно, что ожидаемый выигрыш первого иг­рока линейно зависит от x ₁. На оси X ₁ построим выражения ожидаемых выигрышей первого игрока.

Первый игрок должен выбирать такие стратегии, чтобы максимизировать свой минимальный ожидаемый выигрыш. Поэтому оптимальная стратегия первого игрока определяется как точка пересечения прямых, максимизирующих его мини­мальный ожидаемый выигрыш.

Аналогично находим оптимальную стратегию второго иг­рока. Она определяется как точка пересечения прямых, мини­мизирующих его максимальные ожидаемые проигрыши.

Пример 1. Рассмотрим представленную выше игру, заданную платежной матрицей

 

 

Найти оптимальные стратегии игроков и цену игры.

Решение. Обозначим: x ₁ — вероятность применения пер­вым игроком 1-й стратегии, х ₂, х ₃, х ₄ — вероятность исполь­зования первым игроком 2, 3, 4-й стратегий соответственно, причем х ₁ + x ₂ + x ₃ + x ₄ = 1; y ₁ — вероятность применения вторым игроком 1-й стратегии, у ₂, у ₃, y ₄, y ₅ — вероятность использования вторым игроком 2, 3, 4, 5-й стратегий соответ­ственно, причем y ₁ + у ₂ + у ₃ + y ₄ + y ₅ = 1.

Платежная матрица была упрощена путем вычеркивания дублирующих, заведомо невыгодных стратегий. Поэтому x ₂ = x ₄ = y ₁ = y ₂ = y ₃ = 0 и матрица имеет вид

 

 

 

Найдем решение игры (табл. 31.4) графическим методом (рис. 31.1). На оси Х ₁ разместим точки х ₁ = 0 и х ₁ = 1, через которые проведем прямые, перпендикулярные оси Х ₁. Подстав­ляя х ₁ = 0 и x ₁ = 1 в выражение х ₁ +3, найдем значения, кото­рые отложим на соответствующих перпендикулярных прямых. Соединив эти точки, получим прямую.

Аналогично рассмотрим выражение –3 x ₁ + 5.

Оптимальная стратегия первого игрока определится из ра­венства выражений х ₁ + 3 и - 3 х ₁ + 5:

 

Цена игры v = x ₁ + 3 = 1/2 + 3 = 7/2.

 

 

Оптимальная стратегия первого игрока:

 

 

Найдем оптимальную стратегию для второго игрока (табл. 31.5).

 

 

Имеем

 

 

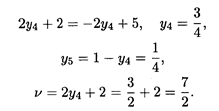
Оптимальная стратегия второго игрока (рис. 31.2):

 

 

 

Пример 2. Найдем решение игры вида (2 х n), заданной пла­тежной матрицей (табл. 31.6)

 

 

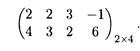
Решение. Находим

α = mах (-1,2) = 2, β = min (4, 3, 3, 6) = 3, 2≤ v ≤ 3.

Тогда

 

 

Оптимальное решение первого игрока:

_опт = (1/2, 1/2), при этом цена игры составляет v = 5/2.

Найдем оптимальное решение второго игрока (табл. 31.7).

Из рис. 31.3 следует, что оптимальная стратегия первого игрока определяется из равенства выражений – x ₁ + 3 и х ₁ + 2, соответствующих 2-й и 3-й чистым стратегиям второго игрока (см. табл. 31.5), поэтому y ₁ = y ₄ = 0, а у ₃ = 1 – y ₂.

 

 

Имеем

 

 

откуда

 

 

 

Оптимальное решение второго игрока (рис. 31.4):

_опт = (0,1 / 2,1 / 2,0), при этом цена игры v = 5/2.

Ответ.

_опт = (1/2, 1/2), _опт = (0,1 / 2,1 / 2,0), v = 5/2.

Пример 3. Найдем решение игры вида (т х 2), заданной пла­тежной матрицей (табл. 31.8)

 

 

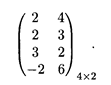
Решение. Находим α = mах (2, 2, 2, -2) = 2, β = min (3, 6) = 3, 2 ≤ v ≤ 3. Пусть y ₁ и у ₂ (причем y ₂ = l — y ₁) — смешанные стратегии второго игрока; x ₁, x ₂, x ₃, x ₄ — смешанные страте­гии первого игрока.

 

 

Находим

 

 

 

Оптимальное решение второго игрока (рис. 31.5):

_опт = (2/3, 1/3), при этом цена игры v = 8/3.

Прямые, пересекающиеся в минимаксной точке, соответ­ствуют 1-й и 3-й чистым стратегиям первого игрока. Это озна­чает, что х ₂ = х ₄ = 0. Следовательно, х ₁ = 1 — x ₃. Найдем оптимальную стратегию 1-го игрока (табл. 31.9, рис. 31.6).

 

 

 

Имеем

 

 

Оптимальное решение первого игрока:

_опт = (1/3, 0, 2/3, 0), при этом цена игры v = 8/3.

Ответ.

_опт = (1/3, 0, 2/3, 0), _опт = (2/3, 1/3), v = 8/3.

 

Решение игр (a_ij)_{m x n} с помощью линейного программирования

 

Теория игр находится в тесной связи с линейным програм­мированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного про­граммирования и решена симплексным методом и, наоборот, задача линейного программирования может быть представле­на как игра.

Для первого игрока математическая модель задачи запи­сывается в виде

 

 

при ограничениях:

 

 

Математическую модель можно упростить, разделив все (п + 1) ограничений на v. Это возможно при v ≠ 0. При v = 0 рекомендуется прибавить любое положительное число ко всем элементам платежной матрицы, что гарантирует положи­тельность значения модифицированной игры. Действительное значение игры получается вычитанием из модифицированного значения этого положительного числа. Если v < 0, то надо сме­нить знаки неравенств. Полагая v > 0, систему ограничений можно записать так:

 

 

Положим Х_i = x_i/v. Так как v → max, то 1 / v → min. Получим задачу линейного программирования вида

 

 

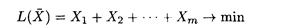
при ограничениях:

 

 

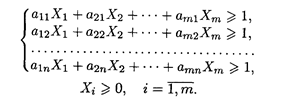
Для второго игрока математическая модель записывается в виде

 

 

при ограничениях:

 

 

где S (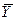) = 1 / v, Y_j = у_j / v.

Задача второго игрока является двойственной по отноше­нию к задаче первого игрока. Можно найти решение одного из игроков, а затем по теоремам двойственности — решение другого.

Применение матричных игр в маркетинговых исследованиях

 

Торговая фирма разработала несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющей­ся конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в табл. 31.10.

Определить оптимальный план продажи товаров.

Решение. Обозначим: вероятность применения торговой фирмой стратегии П ₁ — x ₁, стратегии П ₂ —x ₂, П ₃ — х ₃; ве­роятность использования стратегии К ₁ — у ₁, стратегии К ₂ — y ₂, К ₃ — у ₃.

 

 

Для первого игрока (торговой фирмы) математическая мо­дель задачи имеет вид

 

 

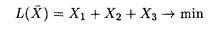
при ограничениях:

 

 

где x_i = Х_iv.

Для второго игрока (конъюнктуры рынка и спроса покупа­телей) математическая модель задачи имеет вид

 

 

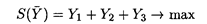
при ограничениях:

 

 

Найдем оптимальное решение задачи для второго игрока симплексным методом. При этом последняя таблица имеет вид табл. 31.11.

Из таблицы следует, что 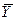_опт = (1/14, 11/196, 5/49), S (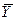)_max = 45/196.

Цена игры v = 1 / S(Y) = 196/45.

Так как у_i = Y_iv, то y ₁ = 14/45, у ₂ = 11/45, у ₃= 20/45.

 

 

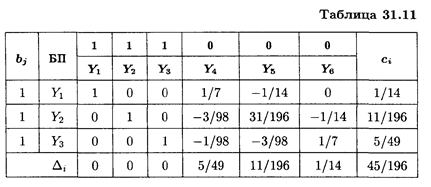
Оптимальная стратегия второго игрока:

 

 

Стратегии первого игрока найдем из последней симплекс­ной таблицы, используя метод соответствия переменных ис­ходной и двойственной задач. Получим

 

 

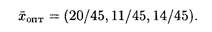
Таким образом, торговая фирма на ярмарке должна при­держиваться стратегии _опт = (20/45, 11/45, 14/45), при этом она получит доход не менее v = 196/45 ден. ед.

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: