Определение производственной программы предприятия в условиях риска и неопределенности с использованием матричных игр

Фирма "Фармацевт" — производитель медикаментов и био­медицинских изделий в регионе. Известно, что пик спроса на некоторые лекарственные препараты приходится на летний пе­риод (препараты сердечно-сосудистой группы, анальгетики), на другие — на осенний и весенний периоды (антиинфекцион­ные, противокашлевые).

Затраты на 1 усл. ед. продукции за сентябрь-октябрь со­ставили: по первой группе (препараты сердечно-сосудистые и анальгетики) — 20 р.; по второй группе (антиинфекционные, противокашлевые препараты) — 15 р.

По данным наблюдений за несколько последних лет служ­бой маркетинга фирмы установлено, что она может реали­зовать в течение рассматриваемых двух месяцев в услови­ях теплой погоды 3050 усл. ед. продукции первой группы и 1100 усл. ед. продукции второй группы; в условиях хо­лодной погоды — 1525 усл. ед. продукции первой группы и 3690 усл. ед. второй группы.

В связи с возможными изменениями погоды ставится за­дача — определить стратегию фирмы в выпуске продукции, обеспечивающую максимальный доход от реализации при цене продажи 40 р. за 1 усл. ед. продукции первой группы и 30 р. — второй группы.

Решение. Фирма располагает двумя стратегиями:

A ₁ — в этом году будет теплая погода;

A ₂ — погода будет холодная.

Если фирма примет стратегию A ₁ и в действительности будет теплая погода (стратегия природы B ₂), то выпущенная продукция (3050 усл. ед. препаратов первой группы и 1100 усл. ед. второй группы) будет полностью реализована и доход со­ставит

 

 

В условиях прохладной погоды (стратегия природы В ₂ ) препараты второй группы будут проданы полностью, а первой группы только в количестве 1525 усл. ед. и часть препаратов останется нереализованной. Доход составит

 

 

Аналогично, если фирма примет стратегию А ₂ и в дейст­вительности будет холодная погода, то доход составит

 

 

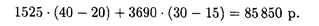
При теплой погоде доход составит

 

 

Рассматривая фирму и погоду в качестве двух игроков, по­лучим платежную матрицу

 

 

Цена игры лежит в диапазоне 16500 р. ≤ v ≤ 77500 р.

Из платежной матрицы видно, что при всех условиях до­ход фирмы будет не меньше 16 500 р., но если погодные условия совпадут с выбранной стратегией, то доход фирмы может со­ставить 77500 р.

Найдем решение игры.

Обозначим вероятность применения фирмой стратегии А ₁через x ₁, стратегии А ₂ — через x ₂, причем х ₁ = 1 — х ₂. Решая игру графическим методом, получим _опт = (0,56; 0,44), при этом цена игры v = 46 986 р.

Оптимальный план производства лекарственных препара­тов составит

 

 

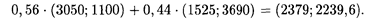
Таким образом, фирме целесообразно производить в тече­ние сентября и октября 2379 усл. ед. препаратов первой группы и 2239,6 усл. ед. препаратов второй группы, тогда при любой погоде она получит доход не менее 46 986 р.

В условиях неопределенности, если не представляется воз­можным фирме использовать смешанную стратегию (догово­ры с другими организациями), для определения оптимальной стратегии фирмы используем критерии природы.

1. Критерий Вальде:

 

 

фирме целесообразно использовать стратегию A ₁.

2. Критерий максимума:

 

 

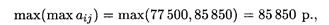
целесообразно использовать стратегию А ₂.

3. Критерий Гурвица: для определенности примем α = 0,4, тогда для стратегии фирмы А ₁

 

 

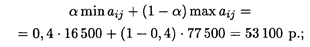
для стратегии А ₂

 

 

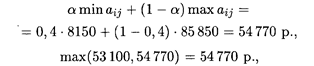
фирме целесообразно использовать стратегию А ₂.

4. Критерий Сэвиджа. Максимальный элемент в первом столбце — 77 500, во втором столбце — 85 850.

Элементы матрицы рисков находятся из выражения

 

 

откуда r ₁₁ = 77500 - 77500 = 0, r ₁₂ = 85 850 - 16 500 = 69 350, r ₂₁ = 77 500 - 8150 = 69 350, r ₂₂ = 85 850 - 85 850 = 0.

Матрица рисков имеет вид

 

 

целесообразно использовать стратегию A ₁ или А ₂.

Следовательно, фирме целесообразно применять страте­гию A ₁ или А ₂.

Отметим, что каждый из рассмотренных критериев не мо­жет быть признан вполне удовлетворительным для оконча­тельного выбора решений, однако их совместный анализ поз­воляет более наглядно представить последствия принятия тех или иных управленческих решений.

При известном распределении вероятностей различных со­стояний природы критерием принятия решения является мак­симум математического ожидания выигрыша.

Пусть известно для рассматриваемой задачи, что вероят­ности теплой и холодной погоды равны и составляют 0,5, тогда оптимальная стратегия фирмы определяется так:

 

 

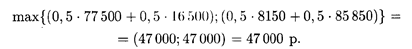
Фирме целесообразно использовать стратегию A ₁ или А ₂.

"Дерево" решений

 

Примеры, которые мы рассматривали до сих пор, включа­ли получение единого решения. Однако на практике результат одного решения приводит к необходимости принятия следую­щего решения и т.д. Эту последовательность принятия реше­ний нельзя выразить таблицей доходов, поэтому приходится использовать другой алгоритм принятия управленческих ре­шений.

Графически подобные процессы могут быть представлены с помощью "дерева" решений. Такое представление облегчает описание многоэтапного процесса принятия управленческого решения в целом.

Рассмотрим "дерево" решений, которое применяют тогда, когда нужно принять несколько взаимосвязанных решений в условиях неопределенности в случае принятия решения, зави­сящего от исхода предыдущего или исходов испытаний.

Составляя дерево решений, рисуют "ствол" и "ветви", ото­бражающие структуру проблемы. Располагают "дерево" ре­шений слева направо. "Ветви" обозначают возможные альтер­нативные решения, которые могут быть приняты, и возмож­ные исходы, возникающие в результате этих решений.

Квадратные "узлы" на дереве решений обозначают места, в которых принимаются решения, круглые "узлы" — места исходов. Так как не представляется возможным влиять на по­явление исходов, то в круглых узлах вычисляют вероятнос­ти их появления. Когда все решения и их исходы указаны на "дереве", оценивается каждый из вариантов и проставляются денежные доходы. Все расходы, вызванные решениями, про­ставляются на соответствующих "ветвях".

Рассмотрим задачу с применением "дерева" решений.

 

Выбор оптимальной стратегии развития предприятия в условиях трансформации рынка

 

Фирма может принять решение о строительстве средне­го или малого предприятия. Малое предприятие впоследствии можно расширить. Решение определяется будущим спросом на продукцию, которую предполагается выпускать на сооружае­мом предприятии. Строительство среднего предприятия эко­номически оправданно при высоком спросе. С другой стороны, можно построить малое предприятие и через два года его рас­ширить.

Фирма рассматривает данную задачу на десятилетний пе­риод. Анализ рыночной ситуации показывает, что вероятности высокого и низкого уровней спроса равны 0,7 и 0,3 соот­ветственно. Строительство среднего предприятия обойдется в 4 млн р., малого — в 1 млн р. Затраты на расширение через два года малого предприятия оцениваются в 3,5 млн р.

Ожидаемые ежегодные доходы для каждой из возможных альтернатив:

— среднее предприятие при высоком (низком) спросе дает 0,9 (0,2) млн р.;

— малое предприятие при низком спросе дает 0,1 млн р.;

— малое предприятие при высоком спросе дает 0,2 млн р. в течение 10 лет;

— расширенное предприятие при высоком (низком) спросе дает 0,8 (0,1) млн р.;

— малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает 0,1 млн р. в год за остальные восемь лет.

Определить оптимальную стратегию фирмы в строительстве предприятий.

Решение. Данная задача является многоэтапной, так как если фирма решит строить малое предприятие, то через два года она может принять решение о его расширении. В этом случае процесс принятия решения состоит из двух этапов: ре­шение в настоящий момент времени о размере предприятия и решение о необходимости его расширения, принимаемое через два года.

На рис. 31.7 задача представлена в виде "дерева" решений. Предполагается, что спрос может оказаться высоким и низ­ким. Дерево имеет два типа вершин: "решающие" вершины, обозначенные квадратными узлами, и "случайные" вершины, обозначенные круглыми узлами.

 

 

Начиная с вершины 1, являющейся "решающей", необходи­мо принять решение относительно размера предприятия. Вер­шины 2 и 3 являются "случайными". Фирма будет рассматри­вать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет устано­вится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или нерасширении предприятия.

Вершины 5 и 6 будут "случайными".

Произведем расчеты для каждой из альтернатив. Вычис­ления начнем со 2-го этапа. Для последних восьми лет альтер­нативы, относящиеся к вершине 4, оцениваются так:

 

 

где ДР — доход с расширением, ДБР — доход без расширения предприятия.

Таким образом, в вершине 4 выгоднее не проводить расши­рение, при этом доход составит l,36 млн р.

Теперь для дальнейших расчетов оставим одну "ветвь", выходящую из вершины 4, которой соответствует доход 1,36 млн р. за остальные восемь лет. Перейдем к вычислениям 1-го этапа. Для вершины 1

 

 

где ДС — доход среднего предприятия, ДМ — доход малого предприятия.

Сравнивая получаемые в вершине 1 доходы среднего и ма­лого предприятий, видим, что более предпочтительным явля­ется вариант строительства среднего предприятия.

Таким образом, фирме целесообразно построить среднее предприятие.

 

Принятие решения о замене оборудования в условиях неопределенности и риска

 

Фирма может принять решение о замене старого оборудо­вания на новое того же вида или его ремонте. Отремонтиро­ванное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.

Решение определяется будущим спросом на продукцию, ко­торую производят на этом оборудовании.

Полная замена оборудования экономически оправданна при высоком уровне спроса. С другой стороны, можно отремонти­ровать старое оборудование и через один год, например, заме­нить его на новое, более совершенное, или заново его отремон­тировать.

В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.

Пример 5. Рассмотрим конкретную задачу о замене оборудо­вания фирмы, представленную в виде "дерева" решений.

Предполагается, что спрос может оказаться высоким, сред­ним и низким.

Дерево имеет два типа вершин: "решающие" и "случай­ные".

 

 

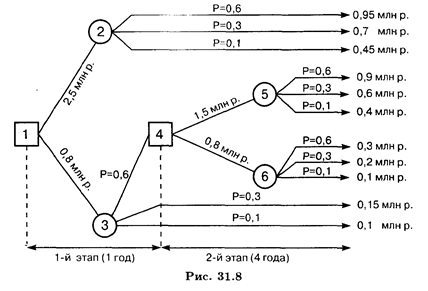
Начиная с "решающей" вершины 1 необходимо принять ре­шение о полной замене оборудования или его ремонте.

Вершины 2 и 3 являются "случайными". Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частич­ной замене старого оборудования более совершенным или ре­монте старого. Вершины 5 и 6 "случайные".

Предположим, что фирма рассматривает эту задачу на пя­тилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса со­ставляют 0,6, 0,3 и 0,1 соответственно. Замена новым обору­дованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого — в 0,8 млн р.

Затраты на частичную замену оборудования на более со­вершенное, чем старое, оцениваются в 1,5 млн р., а повторный ремонт старого — в 0,8 млн р.

Ежегодные доходы для каждой стратегии фирмы следую­щие.

1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса дает 0,95; 0,7 и 0,45 млн р. соответственно.

2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается в 0,3; 0,15 и 0,1 млн р. соответственно.

3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит 0,9; 0,6 и 0,4 млн р. соответственно.

4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3; 0,2 и 0,1 млн р. соответственно.

Определить оптимальную стратегию фирмы в замене обо­рудования.

Решение. Оценим результаты каждой стратегии и опре­делим, какие решения следует принимать в "решающих" вершинах 1 и 4.

Вычисления начнем с этапа 2. Для последних 4 лет альтер­нативы, относящиеся к вершине 4, оцениваются так:

 

 

где ДЧЗ — доход от частичной замены оборудования на более совершенное, ДДР — доход от замены оборудования, прошед­шего дважды ремонт. Так как ДЧЗ > ДДР, то в вершине 4 выгоднее произвести частичную замену оборудования на более совершенное, при этом доход составит 1,54 млн р.

Для дальнейших расчетов в вершине 4 можно оставить од­ну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.

Вычислим доходы на 1-м этапе для "решающей" верши­ны 1:

 

где ДЗН — доход от замены старого оборудования на новое того же вида, ДЗО — доход от отремонтированного оборудо­вания и дальнейшей замены на более совершенное.

Так как ДЗН > ДЗО, то оптимальным решением в верши­не 1 является полная замена старого оборудования на новое того же вида.

Ответ: Оптимальной стратегией фирмы в замене обору­дования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.

Пример 6. Рассмотрим 3´3 игру, заданную матрицей

А =

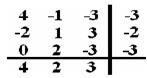Применив предложенный алгоритм, получим:

a = -2, соответствующая стратегия А₂

b = 2, соответствующая стратегия В₂

 

Если a = b, или подробнее, max min a_ik = min max a_ik,

то ситуация {A_i, B_k} оказывается равновесной, и ни один из игроков не заинтересован в том, чтобы ее нарушить.

В том случае, когда нижняя цена игры равна верхней цене игры, их общее значение называется просто ценой игры и обозначается u.

Цена игры совпадает с элементом a_ik матрицы игры, расположенным на пересечении i-той строки (стратегия A_i игрока А) и k-го столбца (стратегия B_k игрока В) – минимальным в своей строке и максимальным в своём столбце.

Этот элемент называют седловой точкой матрицы игры, или точкой равновесия, а про игру говорят, что она имеет седловую т очку.

Стратегии А_i и В_k соответствующие этой седловой точке, называются оптимальными, а совокупность оптимальных ситуаций и цена игры – решением матричной игры с седловой точкой.

Пока игроки придерживаются этих стратегий, средний выигрыш равен 1 (-2<1<2).

Однако если игроку В станет известно, что игрок А придерживается стратегии А₂, он немедленно ответит стратегией В₁ и сведёт его выигрыш к проигрышу – 2. В свою очередь, на стратегию В₁ у игрока А есть стратегия А₁, дающая ему выигрыш 4.

Для построения решений 2´n и m´2 игр существует эффективный метод, основанный на простых геометрических соображениях. Этот метод называют графическим. Рассмотрим его на примере:

Пример 7. Дана 2´6 игра, заданная матрицей

Решение: Составляем таблицу вида:

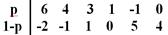
, где р – оптимальное значение.

На основе таблицы составим уравнения, графиками которых будут прямые:

(1): w = 6р – 2(1 – р),

(2): w = 4р – (1 – р),

(3): w = 3р + 5(1 – р),

(4): w = р,

(5): w = -р + 5(1 – р),

(6): w = 4(1 – р).

 

 

т. С является наивысшей точкой огибающей, точкой пересечения прямых (5) и (4), т.е.

 

Тем самым цена игры u= , а оптимальная стратегия

 

р = {p, 1- p} = .

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: