 |
Задание 1. Построить интервальный вариационный ряд распределения
|
|
|
|
Лабораторная работа №1
По математической статистике
Тема: Первичная обработка экспериментальных данных
2. Содержание работы.. 1
3. Оценка в баллах. 1
4. Содержание и форма отчета. 1
5. Контрольные вопросы.. 2
6. Методика выполнения лабораторной работы.. 3
7. Варианты заданий. 10
8. Рекомендуемая литература. 16
Цель работы
Приобретение навыков первичной обработки эмпирических данных методами математической статистики.
Содержание работы
На основе совокупности опытных данных выполнить следующие задания:
Задание 1. Построить интервальный вариационный ряд распределения.
Задание 2. Построить гистограмму частот интервального вариационного ряда.
Задание 3. Составить эмпирическую функцию распределения и построить график.
Задание 4. Рассчитать основные числовые характеристики вариационного ряда:
а) моду и медиану;
б) условные начальные моменты;
в) выборочную среднюю;
г) выборочную дисперсию, исправленную дисперсию генеральной совокупности, исправленное среднее квадратичное отклонение;
д) коэффициент вариации;
е) асимметрию;
ж) эксцесс;
Задание 5. Определить границы истинных значений числовых характеристик, изучаемой случайной величины с заданной надёжностью.
Задание 6. Содержательная интерпретация результатов первичной обработки по условию задачи.
Оценка в баллах
Задания 1-5 – 6 баллов
Задание 6 – 2 балла
Защита лабораторной работы (устное собеседование по контрольным вопросам и лабораторной работе) - 2 балла
Содержание и форма отчета
Работа сдается в письменной форме на листах формата А4 и включает:
1) Титульный лист (Приложение 1)
2) Исходные данные.
3) Представление работы по указанному образцу.
|
|
|
4) Результаты расчетов (выполненные вручную и/или с помощью MS Excel) в указанном порядке.
5) Выводы - содержательная интерпретация результатов первичной обработки по условию задачи.
6) Устное собеседование по работе и контрольным вопросам.
5. Контрольные вопросы
- Какая совокупность называется генеральной (выборочной)?
- Какая выборка называется репрезентативной?
- Какие способы формирования выборки вы знаете?
- Когда выборка называется повторной (бесповторной)?
- Какие вариационные ряды вы знаете?
- Можно ли от дискретного ряда перейти к интервальному и наоборот?
- От чего зависит число интервалов группировки?
- Как от простой статистической таблицы данных перейти к вариационному ряду?
- Как графически изобразить дискретный (непрерывный) вариационный ряд?
- Каким свойством обладает выборочное среднее?
- Как вычислить моду и медиану дискретного (интервального) вариационного ряда?
- Как вычислить дисперсию (среднее квадратичное отклонение) выборочной совокупности?
- Какими свойствами обладает дисперсия?
- Что характеризует коэффициент асимметрии?
- Что характеризует эксцесс?
- Какое число принимается в качество ложного нуля?
- По каким формулам от числовых характеристик, вычисленных в условных вариантах производится переход к числовым характеристикам в первоначальных вариантах?
- Какая оценка называется точечной?
- Что является несмещенной оценкой математического ожидания генеральной совокупности?
- Как вычисляется несмещенная оценка дисперсии генеральной совокупности?
- Какая оценка называется интервальной?
- Какая вероятность называется надежностью? Дайте пояснения на графике нормального закона распределения.
- По каким формулам находится доверительный (надежностный) интервал для генеральной средней и генерального среднеквадратичного отклонения?
- Как определить минимальный объем выборки, чтобы с заданной надежностью
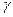гарантировать определенную точность D вычисления генеральной средней? - Как ведет себя предельная ошибка
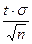(точность оценки), если надежность увеличивается?
|
|
|
Методика выполнения лабораторной работы
Задание 1. Построить интервальный вариационный ряд распределения
Для того, чтобы статистические данные представить в виде вариационного ряда с равноотстоящими вариантами необходимо:
1.В исходной таблице данных найти наименьшее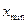 
и наибольшее 
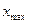значения.
2.Определить размах варьирования: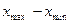 
3. Определить длину интервала h, если в выборке до 1000 данных, используют формулу: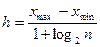 
, где n – объем выборки – количество данных в выборке; для вычислений берут 
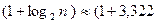lgn).
Вычисленное отношение округляют до удобногоцелого значения.
4. Определить начало первого интервала для четного числа интервалов рекомендуют брать величину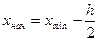 
; а для нечетного числа интервалов 
.
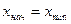5. Записать интервалы группировок и расположить их в порядке возрастания границ
, 
,………., 
,
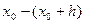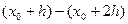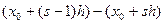где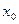 
- нижняя граница первого интервала. За 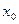берется удобное число не большее 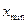, верхняя граница последнего интервала должна быть не меньше 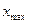. Рекомендуется, чтобы интервалы содержали в себе исходные значения случайной величины и выделять от 5 до 20 интервалов.
6. Записать исходные данные по интервалам группировок, т.е. подсчитать по исходной таблице число значений случайной величины, попадающих в указанные интервалы. Если некоторые значения совпадают с границами интервалов, то их относят либо только к предыдущему, либо только к последующему интервалу.
Замечание 1. Интервалы необязательно брать равными по длине. На участках, где значения располагаются гуще, удобнее брать более мелкие короткие интервалы, а там где реже - более крупные.
Замечание 2. Если для некоторых значений получены “нулевые”, либо малые значения частот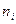 
, то необходимо перегруппировать данные, укрупняя интервалы (увеличивая шаг 
).
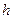Вариант №0
Даны результаты измерения роста (с точностью до см) 60 наудачу отобранных студентов:
178, 160, 154, 183, 155, 153, 167, 186, 163, 155,
157, 175, 170, 166, 159, 173, 182, 167, 171, 169,
179, 165, 156, 179, 158, 171, 175. 173, 164, 172
178, 160, 154, 183, 155, 153, 167, 186, 163, 155,
157, 175, 170, 166, 159, 173, 182, 167, 171, 169,
179, 165, 156, 179, 158, 171, 175. 173, 164, 172
|
|
|
Решение.
1. n=60;: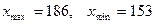 
.
Длина частичного интервала: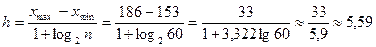 
Примем h = 6. Начало первого интервала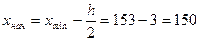 
Исходные данные разбиваем на 6 (m = 1 + log230 = 5,907 ≈ 6) интервалов:
[150,156), [156,162), [162,168), [168,174), [174, 180), [180, 186).
Подсчитав число студентов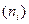 
, попавших в каждый из полученных промежутков, получим интервальный вариационный ряд, который записывается в виде таблицы.
Таблица 1.
| Х | [150,156) | [156,162) | [162,168) | [168,174) | [174, 180) | [180, 186] |
(частота)
|
|
|
|
