 |
Задание 2. Построить гистограмму частот интервального вариационного ряда
|
|
|
|
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению  (плотность частоты).
(плотность частоты).
Площадь частичного i-го прямоугольника равна  сумме частот вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.
сумме частот вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.
Решение.
Длина интервала h = 6. Найдем плотность частоты 
Таблица 2.
| Х | [150,156) | [156,162) | [162,168) | [168,174) | [174, 180) | [180, 186] |
 (частота) (частота)
| ||||||

| 8/6 ≈ 1,4 | 10/6 ≈ 1,65 | 12/6 = 2,0 | 14/6 ≈ 2,3 | 10/6 ≈1,65 | 6/6 = 1 |
Построим на оси 0х заданные интервалы. На оси 0у отложим плотность частоты. Над каждым интервалом на оси 0х проведем соответствующие параллельные отрезки.
 |
Задание 3. Записать эмпирическую функцию распределения
и построить ее график
Одним из способов обработки вариационного ряда является построение эмпирической функции распределения. Эмпирическая функция распределения  , определяет для каждого значения х относительную частоту события Х < x.
, определяет для каждого значения х относительную частоту события Х < x.
 относительная частота (частость)
относительная частота (частость)
Для построения графика эмпирической функции распределения переходят к дискретному ряду распределения, для этого в качестве вариант 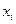 принимают середины частичных интервалов. Частоты при этом не изменяются.
принимают середины частичных интервалов. Частоты при этом не изменяются.
Решение.
Вычислим:
- середину каждого интервала 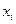 и запишем эти значения в первую строку таблицы;
и запишем эти значения в первую строку таблицы;
- относительные частоты  и запишем в третью строку таблицы;
и запишем в третью строку таблицы;
- накопительные частоты  и запишем в четвертую строку таблицы.
и запишем в четвертую строку таблицы.
Таблица 3.
Значение признака 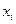 (середина интервала) (середина интервала)
| |||||||
 (частота)
(частота)
| |||||||
 (относительная частота)
(относительная частота)
| 8/60 ≈ 0,133 | 10/60 ≈ 0,167 | 12/60 = 0.2 | 14/60 ≈ 0,233 | 10/60 ≈ 0,167 | 6/60 = 0,1 | |
Накопительные относительные частоты

| 0,133 | 0,133+0,167= 0,3 | 0,133+0,167+0,2= 0,5 | 0,733 | 0,9 | ||
Запишем эмпирическую функцию:
 На оси 0х отметим значения На оси 0х отметим значения 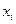 , на оси 0у – накопительные частоты. , на оси 0у – накопительные частоты.
| 
| ||||||
Задание 4. Рассчитать основные числовые характеристики вариационного ряда
|
|
|
Значение признака 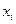
| ||||||
 (частота)
(частота)
|
4а) Мода – это варианта, имеющая наибольшую частоту.
 = 171,
= 171, 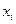 = 171,
= 171,  = 14.
= 14.
Медиана – это варианта, которая делит вариационный ряд на две части, равные по числу вариант.
Если число интервалов четное, то медиана определяется как среднее арифметическое серединных значений. (153+159+165+171+177+183)/6=168, 
Для определения остальных числовых характеристик воспользуемся методом произведений.
Введем условные варианты.  ,где С – «ложный нуль».
,где С – «ложный нуль».
Чаще всего в качестве ложного нуля принимается либо варианта, находящаяся в середине вариационного ряда, либо мода  (варианта
(варианта  , имеющая наибольшую частоту), либо любое другое число, упрощающее расчеты.
, имеющая наибольшую частоту), либо любое другое число, упрощающее расчеты.
Если за  принять какое - либо значение
принять какое - либо значение  , то соответствующая ему условная варианта
, то соответствующая ему условная варианта 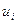 будет равна нулю, а слева и справа от нуля будут располагаться соответственно значения
будет равна нулю, а слева и справа от нуля будут располагаться соответственно значения  1,
1,  2,
2,  3,
3,  4 и т.д.
4 и т.д.
В нашем примере С = 171, h = 6. Составим расчетную таблицу:
Таблица 4.
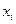
| 
| 
| 
| 
| 
| 
| ni(ui +1)4 |
| -3 | -24 | -216 | |||||
| -2 | -20 | -80 | |||||
| -1 | -12 | -12 | |||||
 = 60 = 60
|  = -34 = -34
|  = 158 = 158
|  = - 250 = - 250
|  = 926 = 926
| ∑= 798 |
 Проверка.
Проверка.
926+4*(-250)+6*158+(-34)+60= -74+948+26=798
4б) Условные начальные моменты найдем по формулам:








4в) Выборочная средняя  Þ
Þ 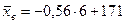 = 167,6
= 167,6
4г) Дисперсия (рассеивание) – характеристика рассеяния значений случайной величины Х около ее математического ожидания.
|
|
|
Выборочная дисперсия

 =
=  ≈ 82,4
≈ 82,4
Среднее квадратичное отклонение также служит для оценки рассеяния случайной величины Х вокруг ее среднего значения 
 ≈ 9,1
≈ 9,1
Исправленная дисперсия генеральной совокупности
 = 60/59*82,4 ≈ 83,7966
= 60/59*82,4 ≈ 83,7966
Исправленное среднее квадратичное отклонение 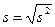 ≈ 9,15
≈ 9,15
4д) Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратичного отклонения к выборочной средней.
 ;
; 
4е) Асимметрия – характеризует «скошенность» кривой распределения относительно математического ожидания. Асимметрия равна нулю, если кривая распределения симметрична относительно математического ожидания; асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой распределения расположена слева от математического ожидания (рис.1а)
Для вычисления асимметрии и эксцесса найдем центральные моменты:
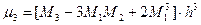
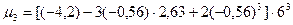 ≈ - 34,56
≈ - 34,56

 ≈ 13478,4
≈ 13478,4
Асимметрия 
 ≈ 0,05
≈ 0,05
4и) Эксцесс – это характеристика большего или меньшего подъема кривой исследуемого распределения по сравнению с нормальной кривой распределения. Если эксцесс равен нулю, то кривая распределения является нормальной кривой; если эксцесс положителен, то кривая распределения имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицателен, то кривая распределения имеет более низкую и «плоскую» вершину, чем нормальная кривая (рис. 1б).
 ;
; 
 | ||||||
|
|
|
|
|


