Пример решения поставленной задачи

Функцию варианта задания оформляем как процедуру - функции, используя в меню оболочки QBasic.

· дифференциальное уравнение (Y¢(x))

FUNCTION f (x, y0)

f = < функция соответствующего варианта >

END FUNCTION

• интервал (а, b), шаг (h), краевое значение функции (у0)
Блок-схема для задачи решения дифференциального уравнения имеет вид.

БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ

 

 

 

Запись всех подпрограмм можно осуществить через меню оболочки QBasic:

1. Alt - вход в меню

2. Edit®New SUB … - создание новой подпрограммы

3. Edit®New FUNCTION… - создание новой подпрограммы функции

4. Набираем в диалоговом окне новое имя подпрограммы (например: eiler)

На экране появляется заготовка для создания подпрограммы:

SUB <имя подпрограммы, параметры>

<текст подпрограммы>

END SUB

1. Приступаем к написанию подпрограммы между ключевыми словами SUB и END SUB

2. Все вспомогательные подпрограммы объединяются управляющей программой или головным модулем.

3. Переход от текста управляющей программы к текстам подпрограммам происходит при нажатии клавиш F2.

ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC

Головной модуль на языке QBasic

DECLARE SUB eiler (a!, b!, h!, y0!)

DECLARE SUB koshi (a!, b!, h!, y0!)

DECLARE SUB runge (a!, b!, h!, y0!)

DECLARE FUNCTION f! (x!, y0!)

CLS

DIM SHARED eilerM(1000), koshiM(1000), rungeM(1000)

INPUT "левый конец интервала a= "; a

INPUT "правый конец интервала b= "; b

INPUT "шаг "; h

INPUT "краевое значение функции Y0= "; y0

yy = y0 'сохранение краевого значения функции

REM Вызов Метода Эйлера

CALL eiler(a, b, h, yy)

yy = y0

 

REM Вызов Метода Эйлера-Коши

CALL koshi(a, b, h, yy)

yy = y0

REM Вызов Метода Рунге-Кутта

CALL runge(a, b, h, yy)

PRINT "--------------------------------------------------------------"

PRINT "│ x │ elier │ koshi │ runge │"

PRINT "--------------------------------------------------------------"

L$ = "│ #.# │ ##.##### │ ##.##### │ ##.##### │"

i = 1

FOR x = a TO b + h / 2 STEP h

PRINT USING L$; x; eilerM(i); koshiM(i); rungeM(i)

i = i + 1

NEXT x

PRINT "--------------------------------------------------------------"

END

Первые четыре строчки пишутся автоматически при присоединении подпрограмм к головному модулю в результате выполнения команды Save All.

Подпрограмма для решения дифференциального уравнения
методом Эйлера:

SUB eiler (a, b, h, y0)

i = 1

eilerM(i) = y0

FOR x = a TO b + h / 2 STEP h

y = y0 + h * f(x, y0)

y0 = y

i = i + 1

eilerM(i) = y0

NEXT x

END SUB

Подпрограмма для решения дифференциального уравнения
методом Эйлера-Коши:

SUB koshi (a, b, h, y0)

i = 1

koshiM(i) = y0

FOR x = a TO b + h / 2 STEP h

k1 = h * f(x, y0)

k2 = h * f(x + h, y0 + k1)

y = y0 + (k1 + k2) / 2

y0 = y

i = i + 1

koshiM(i) = y0

NEXT x

END SUB

Подпрограмма для решения дифференциального уравнения
методом Рунге-Кутта:

SUB runge (a, b, h, y0)

i = 1

rungeM(i) = y0

FOR x = a TO b + h / 2 STEP h

k1 = h * f(x, y0)

k2 = h * f(x + h / 2, y0 + k1 / 2)

k3 = h * f(x + h / 2, y0 + k2 / 2)

k4 = h * f(x + h, y0 + k3)

y = y0 + (k1 + 2 * k2 + 2 * k3 + k4) / 6

y0 = y

i = i + 1

rungeM(i) = y0

NEXT x

END SUB

Процедура функция:

FUNCTION f (x, y0)

f = < функция соответствующего варианта >

END FUNCTION

Построение в Excel графика решений

1. Для построения графика в Excel следует:

2. Набить таблицу значений из Qbasic (в каждом столбце результат решения дифференциального уравнения соответствующим методом).

X	Метод Эйлера	Метод Эйлера-Коши	Метод Рунге-Кутта
0,5	0,672484	0,678814	0,678894
0,6	0,757629	0,770744	0,770909
0,7	0,855875	0,876242	0,876498
0,8	0,967663	0,995754	0,996108
0,9	1,093427	1,129714	1,130172
	1,233588	1,278529	1,279097
1,1	1,388542	1,44257	1,443255
1,2	1,558648	1,622153	1,62296
1,3	1,74421	1,817519	1,818455
1,4	1,945463	2,028813	2,029882
1,5	2,162545	2,256061	2,257268

 

1. Выделить столбцы три столбца – Метод Эйлера, метод Эйлера-Коши, метод Рунге-Кутта.

2. Дальше в меню выбрать: Вставка ® Диаграмма.

3. Появиться меню «Мастера диаграмм».

4. Выбрать: на вкладке «Стандартные» ® График ® График с маркерами, помечающими точки данных ® Далее.

5. Откроется окно «Исходные данные».

6. В окне «Исходные данные», выбрать вкладку Ряд ® Подписи оси Х, нажать маркер . Рисунок 1.

Рисунок 1.

1. Выделить столбец Х, только цифры. Нажать® Далее.

2. Легенду разместить в низу. Нажать ®Далее ® Готово (рис.1)

3. Добавить Линию тренда, уравнение и R². (рис.2)

Рисунок 1

Рисунок 2

Контрольные вопросы

Метод Эйлера

1. Что является решением дифференциального уравнения?

2. Необходим ли поиск начальных условий в методе Эйлера?

3. К какой группе относится модифицированный метод Эй­лера?

4. Почему точность метода Эйлера пропорциональна h, а мо­дифицированного — h2?

5. Метод Эйлера относится к одно шаговым методам. В чем ос­новное отличие одно- и многошаговых методов?

6. Можно ли методом Эйлера решать системы дифференциаль­ных уравнений?

7. Можно ли использовать метод Эйлера для решения задач, не относящихся к задачам Коши?

8. Обязательно ли необходимо задание начальных условий при решении дифференциального уравнения методом Эйлера?

9. В чем заключается отличие явных и неявных вычислитель­ных схем в модифицированном методе Эйлера?

10. Можно ли оценить погрешность решения дифференциально­го уравнения, не зная точного решения?

Метод Рунге — Кутта

1. Сколько раз необходимо на каждом шаге вычислять правую часть уравнения при использовании метода четвертого по­рядка?

2. Как можно оценить погрешность решения дифференциаль­ного уравнения при использовании метода Рунге — Кутта?

3. Можно ли задавать погрешность решения при автоматиче­ском подборе шага в относительных величинах?

4. Сколько предыдущих значений функции нужно иметь, чтобы сосчитать одно следующее значение?

5. К какой группе методов (аналитические или численные) от­носится имеющий аналитическое выражение от искомого значения функции метод Рунге — Кутта?

6. Как записывается рекуррентная формула метода четвертого порядка?

7. Что можно отнести к недостаткам метода, например, самого распространенного четвертого порядка?

8. Как зависит погрешность метода от величины шага решения?

9. Возможно ли применение переменного шага в методе Рунге — Кутта?

Варианты заданий к лабораторной работе

№ п/п	Уравнение	Начальные значение	Конечное значение	Шаг	Начальное значение функции Y
1.	Y' = y + e2x		1,5	0.16	Y(0)=3
2.	Y' = cos(x) - y			0.2	Y(0)=1.5
3.	Y' =			0,2	Y(0)=0
4.	Y' = x2 -	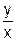		0,2	Y(1)=1
5.	Y' = e2x - 3y			0,2	Y(0) = 0
6.	Y' =			0,2	Y (0) = 2
7.	Y' = ex – x + 2y			0,2	Y (0) = 0
8.	Y' =			0,2	Y (0) = 1
9.	Y' =			0,2	Y (1)=1
10.	Y' = -4y + sin(2x)			0,2	Y(0) = 1
11.	Y' = -y + e-xcos(x)			0,1	Y(0) = 0
12.	Y' = -y + 1-ex			0,2	Y(0) = 2,5
13.	Y' = -y + excos(x)			0,2	Y(0) = 0
14.	Y' = -y – sin(xex)			0,1	Y(0) = 1
15.	Y' = xy			0,2	Y(0) = 1
16.	Y' = x+	1,7		0,1	Y0(1,7) = 5,3
17.	Y' =	1,8	2,5	0,15	Y0(1,3) = 4,5
18.	Y' =	3,1	5,4	0,1	Y0(3) = 5
19.	Y' =		1,5	0,3	Y0(1) = О,5
20.	Y' = 2x + sin	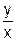0,1		0,05	Y0(0,1)=1
21.	Y' =			0,1	Y0(0) = 0
22.	Y' =			0,1	Y0(0) = 0
23.	Y' =	0,1		0,1	Y0(0,1)=1
24.	Y' = x-y			0,1	Y0(0) = 0
25.	Y' =		0,5	0,1	Y0(0,1)=1
26.	Y' = 2xy			0,05	Y0(0) = 1
27.	Y' = 2x – 3y			0,05	Y0(0) = 1

 

ЛАБОРАТОРНАЯ РАБОТА № 5
Символьные переменные

Цель работы

Ознакомление с принципами программирования задач с символьными переменным.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: