Решение дифференциальных уравнений

Дифференциальные уравнения очень часто встречаются при построении

моделей динамики объектов исследования. Они описывают, как правило, изменения параметров объекта во времени. Результатом решения дифференциальных уравнений являются функции, а не числа, как при решении конечных уравнений, вследствие чего методы решения их более трудоемки.

Дифференциальные уравнения описывают также процессом, тепло-массообмен, изменение концентрации вещества, процессы кристаллизации сахара и многие другие. При использовании численных методов решения дифференциальных уравнений:

или y^’= f (x,y) представляется в табличном виде, т.е. получается
dx совокупность значений Y_i и X_i.

Решение носит шаговый характер, т.е. по одной или нескольким начальным точкам (х, у) за один шаг находят следующую точку и т.д. Разница между двумя соседними значениями аргумента h = x_i+1 - x_i называется шагом.

Наибольшее распространение имеют задачи Коши, в которых заданы начальные условия: при x = x₀, y(x₀) = y₀ . Имея их, легко начинать процесс решения, т.е. найти при x₁ , y₂ - при х₂ и т.д.

Основная идея получения простейших вычислительных алгоритмов в одношаговых методах сводится к разложению исходного решения у(х) в ряд Тейлора.

Количество оставленных членов ряда определяет порядок и, следовательно, точность метода. По полученному разложению, зная значения у в точке разложения у_i и производную f(x_i, y_i), находят значения у через шаг h:
y_i+1 = y_i + ∆y_{i .}

Если в разложении удерживается большее число членов, то необходимо рассчитывать f(x_i, y_i) в несколько точках (таким способом избегают необходимости прямого вычисления высших производных, присутствующих в разложении в ряд Тейлора).

Расчётные алгоритмы многошаговых методов базируются на построении интерполяционных или аппроксимирующих функций, от которых берётся интеграл.

Численными методами решаются не только отдельные уравнения, но и системы уравнений (чаще всего первого порядка), причем большинство методов решения одного уравнения легко распространяются на решения систем.

К классу одношаговых методов относятся методы Эйлера,
Рунге – Кутта и Эйлера-Коши.

Функциональное уравнение у¢ = f(x,у), связывающее между собой независимую переменную, искомую функцию у(х) и ее производную у (х), называется дифференциальным уравнением 1-го порядка.

Решением (частным) решением уравнения на интервале (а, b) называется любая функция у = (х), которая, будучи подставлена в это уравнение вместе со своей производной ¢ (x)обращает его в тождество относительно xÎ(а,b). Уравнение Ф. (х,y) = 0, определяющее это решение как неявную функцию, называется интегралом дифференциального уравнения. На плоскости с фиксированной декартовой прямоугольной системой координат уравнение Ф (х,y) =0 определяет некоторую кривую, которая называется интегральной кривой дифференциального уравнения.

Если в дифференциальном уравнении у¢ = f(x,у) функция f(x,у) непрерывна в некоторой области D, плоскости Оху и имеет в этой области ограниченную частную производную (x,y), то для любой точки (x₀,y₀) Î D, в некотором интервале х₀ — h £ х £ х₀ + h, существует и притом единственное решение у (х) этого уравнения, удовлетворяющее начальному условию

у (х_о) - у_о.

Это утверждение известно как теорема Коши о существовании и единственности решения дифференциального уравнения с заданным начальным условием.

Для задач подобного типа, выделенных в целый класс задач Коши, помимо аналитических методов решения разработаны методы численного решения.

Метод Эйлера

Значения искомой функции у= у (х) на отрезке [x₀,X] находят по формуле:

y_k+1 = y_k + h×f(x_k, y_k), (1)

где у_к = у (х_к), х_к+1 = x_k + h, (х_п = Х), k = 0,1,2,...n -1 и h =

По заданной предельной абсолютной погрешности e начальный шаг вычислений h устанавливают с помощью неравенства h² < .

Метод Эйлера - Коши

Для вычисления значений функции у= у (х) применяют формулу:

(2)

где , , ,

По заданной предельной погрешности начальный шаг вычислений h устанавливается с помощью неравенства h³ < .

Метод Руге - Кутта

Значения искомой функции у= у (х) на отрезке [x₀, X] последовательно находят по формулам:

у_к+] = y_k + y_k, k = 0, l, 2,...n – l (3)

где y_k = ( ),

,

,

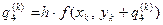
, , h =

По заданной предельной абсолютной погрешности начальный шаг вычислений h устанавливают с помощью неравенства h⁴ < .

Правило Рунге - Ромберга

Пусть и - значения искомой функции, полученные одним из указанных методов при шагах вычисления h и 2h соответственно, а - заданная абсолютная предельная погрешность. Тогда считается, что достигнута заданная точность вычислений, если выполняется неравенство:

(4)

при всех k и при s = 2,3,4 соответственно для методов Эйлера, Эйлера - Коши, Рунге - Кутта. Решением задачи является функция .

Применяя указанное правило, последовательно вычисляют значения искомой функции с шагом 2h и с шагом h и сравнивают полученные результаты по формуле (4). Вычисления заканчивают, когда неравенство (4) выполняется при всех k.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: