 |
Роль поворотного множителя при графическом изображении комплексных чисел
|
|
|
|
Выражение е  называется поворотным множителем и обозначает, что
называется поворотным множителем и обозначает, что
вектор, изображающий комплексное число |А| е  , повернут относительно вещественной полуоси «х» на угол α против направления движения часовой стрелки. Отрицательному значению угла α соответствует поворот вектора по часовой стрелке.
, повернут относительно вещественной полуоси «х» на угол α против направления движения часовой стрелки. Отрицательному значению угла α соответствует поворот вектора по часовой стрелке.
Показатель степени «j α» в выражении е  должен быть отвлеченным числом. Это означает, что угол «α» в выражении «j α» должен быть выражен в радианах. Однако ради большей наглядности допускается запись угла «α» в градусах.
должен быть отвлеченным числом. Это означает, что угол «α» в выражении «j α» должен быть выражен в радианах. Однако ради большей наглядности допускается запись угла «α» в градусах.
При расчетах электрических цепей встречаются случаи вычислений с поворотным множителем, результаты которых полезно запомнить:
1. е 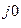 = cos 0 + j sin0 = 1 + 0 = 1;
= cos 0 + j sin0 = 1 + 0 = 1;
2. е  = е
= е 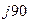 = cos (π / 2) + j sin(π / 2) = 0 + j*1 = j;
= cos (π / 2) + j sin(π / 2) = 0 + j*1 = j;
3. е 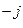 = е
= е 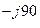 = cos (- π / 2) + j sin(- π / 2) = 0 - j*1 = -j;
= cos (- π / 2) + j sin(- π / 2) = 0 - j*1 = -j;
4. е 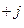 = е
= е 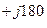 = (е
= (е  )
) 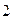 = (j)
= (j) 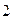 = - 1.
= - 1.
Таким образом, в результате умножения комплексного числа на поворотный множитель е 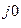 положение вектора, изображающего комплексное число, не изменя
положение вектора, изображающего комплексное число, не изменя
ется, во втором случае направление вектора совпадает с направление полуоси «+j»
(т.е. вектор расположен вверх), в третьем случае вектор расположен вниз, в четвертом случае вектор в результате умножения поворачивается на 180º против часовой стрелке (при + 180º) или по часовой (при - 180º).
В последнем случае направление поворота не имеет значения, т.к. при повороте как против часовой, так и по часовой стрелке, вектор занимает положение, противо
положное исходному.
В конце объяснения представим одно и тоже число А в разных формах:
1. в алгебраической А = 3 + j4;
2. в графической – в виде вектора на рис.2;
3. в тригонометрической А = 5 (cos 53º + j sin53º);
4. в показательной А = 5 е 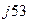 .
.
Таким образом, из четырех форм записи комплексного числа А только две –
|
|
|
алгебраическая и тригонометрическая, строго соответствуют понятию «комплекс-
ное число», т.е. такое число, которое состоит из нескольких частей.
Следует отметить, что при расчетах электрических цепей символическим методом часто приходится переходить от одной формы представления комплекс-
ного числа к другой, например, от алгебраической к показательной. Для таких переходов применяют простейшие действия над числами, а именно: сложение, вычитание, умножение и деление.
Часть 2. Действия с комплексными числами
Сложение и вычитание комплексных чисел
Для сложения и вычитания комплексных величин и чисел используют их алгебра-
ическую и графическую формы представления.
Сложение и вычитание комплексных чисел в алгебраической форме
При сложении комплексных чисел (комплексов) складываются отдельно их вещественные и мнимые составляющие, например,
А + В = (А' + j А") + (В + j В") = (А' + В') + j(А" + В") =
= С + jС" = С (11)
При вычитании комплексных чисел (комплексов) вычитаются отдельно их вещественные и мнимые составляющие, например,
А - В = (А' + j А") - (В + j В") = (А' - В') + j(А" - В") =
= С + jС" = С (12)
Вычитание комплексных чисел можно заменить простейшим действием элементарной алгебры, а именно - сложением уменьшаемого числа с вычитаемым, взятым с обратным знаком:
С = А – В + А + (- В),
или
С = (А' + j А") + (- В – j В") = (А' - В') + j(А" - В") =
= С + jС" = С (13).
Пример 5. Найти сумму С чисел А =3 + j 4 и В = 5 + j 8.
Решение. Сумма С = А + В = 3 + j 4 + 5 + j 8 = 8 + j 12.
Пример 6. Найти сумму С чисел А =4 + j 6 и В = - 5 + j 8.
Решение. Сумма С = А + В = 4 + j 6 + (- 5 + j 8) = -1+ j14.
Пример 7. Найти разность С чисел А = 80 + j 90 и В = 50 – j 30.
Решение. Разность С = 80 + j 90 – (50 – j 30) = 80 + j90 – 50 + j 30 =
= 30 + j120.
Пример 8. Найти сумму С чисел А = 10е 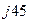 и В = 6е
и В = 6е 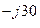 .
.
Решение. Выразим комплексные числа в алгебраической форме:
|
|
|
А = 10е 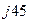 = 10 cos 45º + j10sin 45º = 10*0,707 + j10*0,707 = 7,07 + j7,07
= 10 cos 45º + j10sin 45º = 10*0,707 + j10*0,707 = 7,07 + j7,07
В = 6е 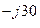 = 6 cos 30º - j6 sin 30º = 6*0,866 – j6*0,5 = 5,2 – j3.
= 6 cos 30º - j6 sin 30º = 6*0,866 – j6*0,5 = 5,2 – j3.
Сумма С = А + В = 7,07 + j7,07 + (5,2 – j3) = 12,27 + j4,07.
Преобразуем число С из алгебраической в показательную форму:
модуль суммы | C | = 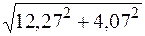 = 12,9;
= 12,9;
тангенс аргумента tg α = C"/ С' = 4,07 / 12,27 = 0,331;
α = arc tg α = arc 0,331 = 18º20';
число С = 12,9е 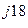
 .
. 
|
|
|


