 |
Сложение и вычитание комплексных чисел в графической форме
|
|
|
|
Каждое комплексное число может быть представлено вектором, поэтому сложению комплексов соответствует сложение векторов.
Действительная составляющая суммарного вектора равна алгебраической сумме действительных составляющих суммируемых векторов (рис.4), т.е.
С' = А' + В' (14)
Аналогично, мнимая составляющая суммарного вектора равна алгебраиче-
ской сумме мнимых составляющих суммируемых векторов (рис. 4), т.е.
С" = А" + В". (15)
Вычитание векторов, представляющих комплексные величины, можно заменить сложением уменьшаемого вектора с вычитаемым вектором, взятым с обратным знаком (рис. 5)

Рис. 4. Сложение векторов А и В Рис. 5. Вычитание вектора В из вектора А
Умножение и деление комплексных чисел
Возможны2 случая умножения и деления комплексов:
1. комплексы заданы в показательной форме;
2. комплексы заданы в алгебраической форме.
2.1. Умножение и деление комплексных чисел в алгебраической форме
Умножение
Перемножим два комплекса, заданных в алгебраической форме: А = А' + jА" и
В = В' + j В".
С = А*В = (А' + j А")*(В' + j В") = А'*В' + А'*j В" + jА"* В' + j 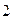 А"*В" =
А"*В" =
= (А'*В' - А"*В") + j (А'*В'' + А"* В') = С' + С" (18).
Пример. Найти произведение комплексов А = 2 + j 4 и В = 8 + j 6.
Решение. С = А*В = (2 + j 4)*(8 + j 6) = (2*8 – 4*6) + j (2*6 +4*8) =
(16 – 24) + (12 + 32) = - 8 + j44.
Деление
Особенностью деления двух комплексов является дополнительное умно-
жение делимого и делителя, т.е. числителя и знаменателя на сопряженный комп-
лекс. Как известно, умножение числителя и знаменателя на одно и то же число не изменяет дробь. Однако в данном случае в результате такого умножения в знаменателе образуется вещественное число, что резко упрощает дальнейший расчет.
|
|
|
Сопряженными называются два таких комплекса, мнимые части которых имеют противоположные знаки.
Пусть имеется комплекс А = А'+ j А", тогда сопряженный с этим числом комплекс Ậ = А' – j А".
Пусть надо разделить комплекс А на комплекс В:
С = А / В = (А'+ j А") / (В'+ j В").
Умножим числитель и знаменатель на сопряженный знаменателю множитель
(В'- j В"):
С = (А'+ j А")*(В'- j В") / (В'+ j В")*(В'- j В") = (А'* В' - j А'* В"+ j А"* В' - j 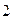 А"* *В") / (В'
А"* *В") / (В' 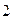 + В"
+ В" 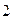 ) = (А'* В' + А"* В") / (В'
) = (А'* В' + А"* В") / (В' 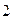 + В"
+ В" 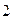 ) + j*(А"* В' - А'* В") / (В'
) + j*(А"* В' - А'* В") / (В' 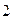 + В"
+ В" 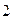 ) = C' + C" (19).
) = C' + C" (19).
Как видим, в знаменателях действительной и мнимой частей находится одно и то же действительное число (В' 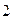 + В"
+ В" 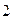 ), что резко упрощает расчет.
), что резко упрощает расчет.
Пример 15. Для комплекса А = 5 + j 8 найти сопряженный комплекс.
Решение. Сопряженный комплекс Ậ = 5 – j 8.
Пример 16. Найти произведение сопряженных комплексов, одним из которых является А = 5 + j 8.
Решение. Ĉ = А* Ậ = (5 + j 8)*(5 – j 8) = 5 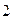 + 8
+ 8 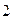 = 25 + 64 = 89.
= 25 + 64 = 89.
Пример 17. Найти частное от деления комплексов А = 6 + j20 и В = 3 + j4.
Решение. С = А / В = (6*3 + 20*4) / (3 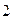 + 4
+ 4 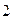 ) + j*(20*3 – 6*4) / (3
) + j*(20*3 – 6*4) / (3 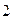 + 4
+ 4 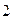 ) =
) =
= (18 + 80) / 25 + j*(60 – 24) / 25 = 3,92 + j 1,44.
Умножение и деление комплексных чисел в показательной форме
Умножение
Перемножим два комплекса, заданных в показательной форме: А = |А|е  и В =
и В =
= |В|е  .
.
Тогда С = А*В = |А|е  *|В|е
*|В|е  = | A*B|е
= | A*B|е  = |C|е
= |C|е  (16),
(16),
откуда |C| = | A*B| и γ = α + β.
Таким образом, произведение двух комплексов представляет собой новый комп-
лекс, модуль которого равен произведению модулей, а аргумент – сумме аргумен-
тов перемножаемых комплексов.
Пример 9. Найти произведение комплексов А = 15е  и В = 5.
и В = 5.
Решение. С = А*В = 15е  *5 = 75е
*5 = 75е  .
.
Пример 10. Найти произведение комплексов А = 30е  и В = 5е
и В = 5е  .
.
Решение. С = А*В = 30 е  *5 е
*5 е  = 150е
= 150е 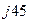 .
.
Пример 11. Найти произведение комплексов А = 70е  и В = 0,5е
и В = 0,5е  .
.
Решение. С = А*В = 70е  *0,5е
*0,5е  = 35 е
= 35 е  ..
..
Деление
Разделим два комплекса, заданных в показательной форме: А = |А|е  и В = |В|е
и В = |В|е  .
.
|
|
|
Тогда С = А/В = |А|е  /|В|е
/|В|е  = | A/B|е
= | A/B|е  = |C|е
= |C|е  (17),
(17),
Откуда |C| = | A/B| и γ = α - β.
Таким образом, произведение двух комплексов представляет собой новый комп-
лекс, модуль которого равен частному от деления модулей, а аргумент – разности аргументов делимого и делителя.
Пример 12. Найти частное от деления комплексов А = 15е  и В = 5.
и В = 5.
Решение. С = А/В = 15е  / 5 = 3е
/ 5 = 3е  .
.
Пример 13. Найти частное от деления комплексов А = 30е  и В = 5е
и В = 5е  .
.
Решение. С = А/В = 30 е  / 5 е
/ 5 е  = 6е
= 6е  .
.
Пример 14. Найти частное от деления комплексов А = 70е  и В = 0,5е
и В = 0,5е  .
.
Решение. С = А/В = 70е  / 0,5е
/ 0,5е  = 140 е
= 140 е  .
.
|
|
|


