 |
Комплексная форма напряжения
|
|
|
|
Рассмотрим комплексную форму напряжения в двух случаях:
1. переменное напряжение изображается вектором, вращающимся с угловой скоростью ω;
2. переменное напряжение изображается неподвижным вектором.
1-й случай (угловая скорость вектора напряжения ω ≠ 0).
Предположим, что напряжение изменяется по закону
u = U 
sin (ωt + ψ) (20),
где: u – мгновенное значение напряжения, В;
U - амплитудное значение напряжение, В;
ω – угловая частота переменного тока, рад / с (с 
);
t – промежуток времени между моментом времени t = 0 и данным моментом,
с;
ψ – начальная фаза напряжения, электрический градус.
Такое напряжение можно представить комплексным числом
Ủ = U *е 
= U cos (ωt + ψ) + j U sin (ωt + ψ) (21).
В правой части этого числа выражение U sin (ωt + ψ) представляет собой мгно-
венное значение синусоидально изменяющегося напряжения. Поскольку в правую часть выражения входит время, эта форма позволяет найти мгновенное значение
напряжения для любого момента времени t. (см. пример 19).
Пример 18. Напряжение изменяется по закону u = 310 sin (314t + 30º). Представить это напряжение в комплексной форме.
Решение. Ủ = 310*е 
.
Пример 19. Напряжение изменяется по закону. Ủ = 310*е 
.
Найти мгновенные значения этого напряжения для моментов времени t = 0; 0,0025 с; 0,005 с; 0,0075 с; 0,01 с; 0,0125 с; 0,015 с; 0,0175 с; 0,02 с.
Решение. Мгновенное значение синусоидально изменяющегося напряжения
u 
= U sin (ωt + ψ) = 310 sin (314t + 30º).
Примечание: для расчета числа sin (314t + 30º) надо перевести радианы
( в данном случае – 314), в градусы. Для этого число радиан (314) умножают на число градусов в одном радиане, т.е. на число 360º/ 2π (1 рад = 360º/ 2π = 57º3').
Для момента времени t = 0
|
|
|
u 
= 310 sin (314*0 + 30º) = 310 sin 30º = 310*0,5 = 155 В.
u 
= 310 sin [314 (360º/ 2π)*0,0025*+ 30º ] = 310 sin(45º + 30º) = 310 sin 75º = 300 В;
u 
= 310 sin [314 (360º/ 2π)*0,005*+ 30º ] = 310 sin(90º + 30º) = 310 sin 120º = 268 В;
u 
= 310 sin [314 (360º/ 2π)*0,0075*+ 30º ] = 310 sin(135º + 30º) = 310 sin 165º = 80 В;
u 
= 310 sin [314 (360º/ 2π)*0,01*+ 30º ] = 310 sin(180º + 30º) = 310 sin 210º = - 15,5 В;
u 
= 310 sin [314 (360º/ 2π)*0,0125*+ 30º ] = 310 sin(225º + 30º) = 310 sin 255º = - 300 В;
u 
= 310 sin [314 (360º/ 2π)*0,015*+ 30º ] = 310 sin(270º + 30º) = 310 sin 300º = - 268 В;
u 
= 310 sin [314 (360º/ 2π)*0,0175*+ 30º ] = 310 sin(315º + 30º) = 310 sin 345º = - 80 В;
u 
= 310 sin [314 (360º/ 2π)*0,02*+ 30º ] = 310 sin(360º + 30º) = 310 sin 390º =
= 155 В.
По найденным числовым значениям при необходимости можно построить волновую (в виде синусоиды) диаграмму данного переменного напряжения u (t).
2-й случай (угловая скорость вектора напряжения ω = 0).
Подставляем ω = 0 во все полученные в 1-м случае соотношения.
Такое напряжение можно представить комплексным числом
Ủ = U *е = U cos (ωt + ψ) + j U sin (ωt + ψ) = U cos (0*t + ψ) + j U sin (0*t + ψ) = U cos ψ + j U sin ψ (22).
В правой части этого числа выражение j U sin ψ - это мгновенное значе-
ние синусоидально изменяющегося напряжения. На комплексной плоскости j (х) это выражение выражается проекцией вектора U на вертикальную ось.
Поскольку в правую часть выражения не входит время (t = 0), это выраже-
ние позволяет найти мгновенное значение напряжения только для момента времени t = 0.
Для действующих значений напряжения получим аналогичное выражение
Ủ = U*е ,
где: U = U / 
- действующее значение напряжения.
Пример 20. Напряжение изменяется по закону u = 310 sin (314t + 30º). Представить это напряжение в комплексной форме.
Решение. Ủ = 310*е 
.
Пример 21. Напряжение изменяется по закону u = 310 sin (314t + 30º). Представить действующее значение этого напряжения в комплексной форме.
Решение. Действующее значение напряжение U = U / = 310 / = 220 В.
Это напряжение в комплексной форме Ủ = 220*е .
|
|
|
Все приведенные выше рассуждения, касавшиеся напряжений, полностью относятся к токам.
Например, если ток изменяется по закону ι = I sin (ωt + ψ), то его можно представить комплексным числом
Ĭ = I *е = I cos (ωt + ψ) + j I sin (ωt + ψ) (23).
Поскольку в правую часть выражения входит время, это выражение позволяет найти мгновенное значение тока для любого момента времени t.
Если принять ω = 0 (вектор тока не вращается), то комплекс такого тока
Ĭ = I *е = I cos ψ + j I sin ψ (24).
Поскольку в правую часть выражения не входит время (t = 0), это выражение позволяет найти мгновенное значение тока только для момента времени t = 0.
2. Комплексная форма сопротивлений и проводимостей
Комплексным сопротивлением электрической цепи называется отношение комплексного напряжения Ủ к комплексному току Ĭ:
Ž = Ủ / Ĭ = U*е / I *е = (U / I)*e = z (cosφ + j sinφ) =
= r + j х (25),
где: Ž – комплексное сопротивление цепи, Ом;
U – модуль комплексного напряжения, равный действующему его значению, В;
I - модуль комплексного тока, равный действующему его значению, А;
z, r и х – полное, активное и реактивное сопротивления цепи, Ом.
При записи сопротивления в комплексной форме вещественная часть комп-
лексного сопротивления всегда равна активному сопротивлению, а мнимая часть – реактивному.
При индуктивной нагрузке мнимая часть комплексного сопротивления положительна, при емкостной – отрицательна.
Пример 22. В цепь переменного тока включены резистор и индуктивность с сопротивлениями r = 3 Ом, х 
= 4 Ом. Представить полное сопротивление цепи в
комплексной форме.
Решение. Полное сопротивление цепи z = r + j х = 3 + j 4 (Ом).
Пример 23. В цепь переменного тока последовательно включены резистор и ем-
кость с сопротивлениями r = 3 Ом, х 
= 4 Ом. Представить полное сопротивление цепи в комплексной форме.
Решение. Полное сопротивление цепи z = r – j х = 3 – j 4 (Ом).
Пример 24. В цепь переменного тока последовательно включены резистор, индуктивность и емкость с сопротивлениями r = 3 Ом, х = 12 Ом и х = 4 Ом. Представить полное сопротивление цепи в комплексной форме.
Решение. Полное сопротивление цепи z = r + j х - j х = r + j х - j х =
= r + j (х - х ) = 3 + j (12 - 4) = 3 + j 8 (Ом).
|
|
|
Пример 25. В цепь переменного тока последовательно включены резистор, индуктивность и емкость с сопротивлениями r = 3 Ом, х = 4 Ом и х = 12 Ом. Представить полное сопротивление цепи в комплексной форме.
Решение. Полное сопротивление цепи z = r + j х - j х = r + j х - j х =
= r + j (х - х ) = 3 + j (4 - 12) = 3 – j 8 (Ом).
Комплексной проводимостью электрической цепи называется отношение комплексного тока Ĭ к комплексному напряжению Ủ:
Ŷ = Ĭ / Ủ = I*е / U*е = (I / U)* е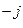 
= (I / U)* е =
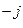= y*е 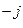= y (cosφ – j sinφ) = g – j b (26),
где: Ŷ - комплексная проводимость, См (1 / Ом);
y – полная проводимость цепи, См;
g – активная проводимость цепи, См;
b - реактивная проводимость цепи, См;
|
|
|
